ТЗ с дополнительным условием: в случае необходимости вывоза всей продукции с определенного склада (удовлетворения всей потребности определенного потребителя) стоимость перевозки с данного склада фиктивному потребителю (перевозки с фиктивного склада данному потребителю) равна M (бесконечно большое число).
Введение такой искусственной переменной позволяет нам взять точку в начале координат, но эта точка не входит в область допустимых решений. Переменная искусственного базиса является стартом для решения задачи симплекс-методом, в процессе решения она выходит из базиса и становится равной 0.
В целевую функцию переменная искусственного базиса записывается с коэффициентом М и вычитается из целевой функции. М – это очень большое число, которое, если tне равняется нулю, не позволяет функции принять максимальное значение.
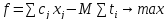 .
.
Т.е. если tне равно нулю, то значение функции только уменьшается.
Алгоритм решения:
Если после введения балансовой переменной в матрице системы ограничений нет достаточного количества столбцов, из которых можно составить единичную матрицу, то в те уравнения, которые не содержат базисной переменной, вводится искусственная переменная t, в каждое своя.
Искусственные переменные вводятся в целевую функцию с положительным большим коэффициентом М со знаком «-» (коэффициент М – одинаков для всех t).
12. Способ задания и основные понятия теории игр.
Предметом изучения теории игр служат ситуации, в которых решение принимается двумя или более участниками, каждый из которых стремится улучшить свое положение за счет другого (конфликтные ситуации). Участники таких ситуаций называются игроками теории игр, а сама ситуация - игрой. Результаты игры (выигрыш или проигрыш игроков) называются платежами. Каждый из игроков имеет несколько возможных вариантов поведения, называемых стратегиями. Игры с двумя участниками, в которых выигрыш одного - это проигрыш другого, называются играми двух лиц с нулевой суммой. Игрок А стремится максимизировать свой минимальный выигрыш, а игрок В - минимизировать максимальный проигрыш. Игрок А – строки, В- столбцы.
14. Антагонистическая (матричная) игра. Ситуация равновесия. Ситуация равновесия в чистых стратегиях.
Один из способов описания игры состоит в том, что рассматривают все возможные стратегии каждого игрока и определяют платеж, соответствующий любой возможной комбинации стратегий всех игроков. Описанная таким образом игра называется игрой в нормальной (прямоугольной) форме.
В общем случае нормальная форма игры двух участников состоит из двух платежных матриц, показывающих, какую сумму получает каждый из игроков при любой из возможных пар стратегий. Эти две матрицы записывают в виде одной общей матрицы, элементами которой является пара чисел, первое из которых определяет величину выигрыша игрока 1, а второе - игрока 2.
Если платежная матрица имеет седловую точку, то говорят, что она имеет ситуацию равновесия в чистых стратегиях и соответствующие стратегии являются равновесными для обоих игроков, соответствующий элемент матричной таблицы – цена игры – равен выигрышу первого в состоянии равновесия и проигрышу второго.
Чтобы определить ситуацию равновесия, нужно найти maxmin (выигрыш, который может гарантировать себе первый игрок независимо от того, что делает второй) и minmax (то, что может заплатить второй игрок (его проигрыш) при любых действиях первого). Если они совпадают, то существует равновесная ситуация в чистых стратегиях. Выигрыш равен соответствующему элементу матрицы и равен цене игры.
Равновесие по Нэшу решение, в котором каждый субъект выбирает наилучший ответ на текущее поведение другого субъекта.

16. Понятие о максимине и минимаксе. Существование точки равновесия в чистых стратегиях.
Игрок А стремится максимизировать свой минимальный выигрыш, а игрок В - минимизировать максимальный проигрыш. Стратегия, при которой выигрывает игрок А называется максиминной, игрок В - минимаксной, а значения игры соответственно максимином и минимаксом. В случае, когда верхняя и нижняя значения игры совпадают, говорят, что минимаксная и максиминная стратегии игроков образуют седловую точку и являются чистыми стратегиями.
Равнове́сиеНэ́ша — концепция решения, одно из ключевых понятий теории игр. Так называется набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники своих стратегий не меняют[1]. Джон Нэш доказал существование такого равновесия в смешанных стратегиях в любой конечной игре.
{\displaystyle i} 
{\displaystyle H_{i}(x^{*})\geq H_{i}(x_{i},x_{-i}^{*}).}
Игра может иметь равновесие Нэша в чистых стратегиях или в смешанных (то есть при выборе чистой стратегии стохастическис фиксированной частотой). Нэш доказал, что если разрешить смешанные стратегии, тогда в каждой игре n игроков будет хотя бы одно равновесие Нэша.
17. (19) (21) (23) М-задача, искусственные переменные. Метод искусственной функции.(Метод штрафных функций). (Признак существования решения исходной задачи). (Признак несовместимости области допустимых решений задачи ЛП).
M-задача
Метод искусственного базиса применяется для решения канонической ЗЛП в случае, когда задача не имеет начального решения с базисом из единичных векторов (ортонормированным базисом).
В этом случае в уравнения, не содержащие базисной переменной, добавляют со знаком «+» неотрицательные переменные, называемые искусственными.
В отличие от дополнительных переменных, искусственные переменные влияют на целевую функцию Z(X), они входят в нее с коэффициентами М, причем в задачу на максимум с коэффициентом –М, в задачу на минимум с коэффициентом +М. Величина М предполагается достаточно большим положительным числом (M>>1), значение которого не задается. Поэтому такая задача носит название М-задачи.
В случае решения задачи на максимум расширенная задача имеет вид:
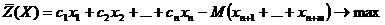
при ограничениях:
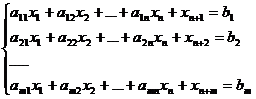
xj≥ 0.
Векторы An+1,An+2,…,An+m называются искусственными векторами. Данная задача имеет начальное опорное решение  с базисом Б = (An+1,An+2,…,An+m) (в этом случае исходный базис целиком состоит из искусственных векторов).
с базисом Б = (An+1,An+2,…,An+m) (в этом случае исходный базис целиком состоит из искусственных векторов).
Справедлива следующая теорема.
- Если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи;
- если в оптимальном решении М-задачи хотя бы одна искусственная переменная отлична от 0, то исходная задача не имеет решения (из-за несовместимости системы ограничений);
- если М-задача не имеет решения из-за неограниченности целевой функции, то и исходная задача решения не имеет.
Особенности алгоритма метода искусственного базиса
- Виду того, что начальное опорное решение расширенной ЗЛП содержит искусственные переменные, входящие в целевую функцию с коэффициентами -М (max) или +М (min), оценка разложений векторов условий Δj= CбXj -cj состоит из двух слагаемых Δj= Δ’j +Δ’’j(M). Т.к. М – велико, то на первом этапе расчета для нахождения векторов, вводимых в базис, используется только слагаемое Δ’’j(M).
- Векторы, соответствующие искусственным переменным, которые выводятся из базиса опорного решения, исключаются из рассмотрения.
- После того как все векторы, соответствующие искусственным переменным, исключены из базиса, расчет продолжается обычным симплексным методом с использованием оценок Δ’j, не зависящих от М.
- Переход от решения расширенной ЗЛП к решению исходной ЗЛП осуществляется с помощью указанных ранее замечаний.

a) Признак существования решения исходной задачи.
Если вспомогательная задача имеет оптимальный план, в котором хотя бы одна искусственная переменная больше нуля, то исходная задача не имеет решения из-за несовместности системы ограничений.
(b) Признак несовместимости области допустимых решений задачи ЛП.
Если М-задача не имеет решения из-за неограниченности вспомогательной целевой функции на множестве допустимых планов, то и исходная задача не имеет решения или из-за неограниченности исходной целевой функции на множестве допустимых планов, или из-за несовместности системы ограничений.
18. Определение смешанной стратегии. Математическое ожидание выигрыша первого игрока в случае смешанных стратегий. Определение точки равновесия в смешанных стратегиях.

Каждая чистая стратегия может рассматриваться как частный случай смешанных стратегий. называется парой оптимальных смешанных стратегий игроков А и В если выполняется. P и Q - множества всех возможных стратегий игроков А и В соответственно.
М - математическое ожидание выигрыша А (проигрыша В).
Равнове́сиеНэ́ша — концепция решения, одно из ключевых понятий теории игр. Так называется набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники своих стратегий не меняют[1]. Джон Нэш доказал существование такого равновесия в смешанных стратегиях в любой конечной игре
20. Теорема о существовании точки равновесия в случае смешанных стратегий. Теорема о цене игры в случае применения одним из игроков чистых стратегий.

Основной теоремой в теории игр двух лиц с нулевой суммой является теорема о минимаксе, согласно которой любая конечная игра имеет решение, если допускается использование смешанных стратегий.
Матричная игра с седловой точкой имеет решение в области чистых стратегий, причем это решение может быть не единственным.
Матричная игра без седловой точки имеет решение, возможно не единственное, при котором хотя бы один из игроков применяет смешанную стратегию.
Равновесие Нэша – существование в смешанных стратегиях Теорема 1 (Теорема Дж. Нэша). Для произвольной дискретной игры существует, по меньшей мере, одно равновесие Нэша в смешанных стратегиях.
22. Графическое решение игры в случае наличия у одного из игроков двух чистых стратегий.



24. Доминирующие и доминируемые стратегии. Упрощение матрицы игры. Вероятности доминируемой стратегии в оптимальной смешанной.
Если для некоторых двоих игроков выполнено неравенство и хотя бы при одном j неравенство выполняется как строгое, то говорят, что стратегия превосходит (доминирует) стратегию.
 Матрица упрощается след. Образом: Вычеркиваются строки, каждый элемент такой строки меньше или равен элементу другой строки).Вычеркиваются столбцы, каждый элемент которого больше или равен элементу другого столбца. Упрощая платежную матрицу, мы приходим в состояние, когда у одного из игроков остается только две стратегии. Тогда возможно решить игру графическим способом.
Матрица упрощается след. Образом: Вычеркиваются строки, каждый элемент такой строки меньше или равен элементу другой строки).Вычеркиваются столбцы, каждый элемент которого больше или равен элементу другого столбца. Упрощая платежную матрицу, мы приходим в состояние, когда у одного из игроков остается только две стратегии. Тогда возможно решить игру графическим способом.
Задача, двойственная данной
Задача, двойственная данной, строится по определению следующим образом:
Если прямая задача на максимум, то двойственная – на минимум.
Если задача на максимум, то ограничения либо в сторону меньше, либо равенства. Соответственно и наоборот: если задача на минимум, то ограничения в сторону больше, либо равенства.
Число переменных двойственной задачи равняется числу ограничений прямой.
Число ограничений двойственной задачи равняется числу переменных прямой.
Матрицы ограничений прямой и двойственной задачи транспонированы относительно друг друга.
Чтобы составить двойственную задачу каждому ограничению прямой задачи сопоставляют переменную двойственной.
Коэффициент целевой функции двойственной задачи равен правым частям ограничений прямой задачи (.
Правые части ограничений двойственной задачи совпадают с коэффициентами целевой функции прямой задачи.
Если ограничение задано в виде неравенства, то двойственная переменная неотрицательна.
Если ограничение задано в виде равенства, то двойственная переменная может принимать любые значения.
Если переменная прямой задачи неотрицательна, то ограничение двойственной заданы в виде неравенства.
Если переменная прямой задачи может принимать любые значения, то соответствующее ограничение двойственной задано в виде равенства.
Задача, двойственная двойственной, является прямой.
26. Связь решения матричной игры с задачей ЛП для первого (второго) игрока
Задачу антагонистической игры можно свести к двум взаимнодвойственным задачам линейного программирования
Пусть дана игровая матрица А’, для которой существуют элементы меньшие или равные нулю.
Нужно перейти к матрице А=А’+сS, где 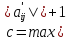 (
(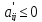 ).
).
Получаем новую матрицу, в которой все элементы уже положительны. Чтобы решить игру нужно найти 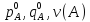 .
.
Для матрицы А нужно составить пару взаимнодвойственных задач:
| Прямая
| Двойственная
|
Y-?
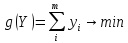
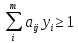
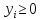
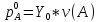 , если , если 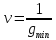
| X-?
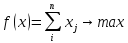
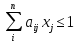
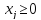
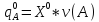 , если , если 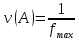
|
Оптимальный вектор для матрицы А равен оптимальному вектору для матрицы А’ (т.е. оптимальные стратегии 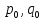 совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
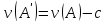 .
.



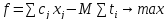 .
.

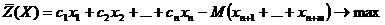
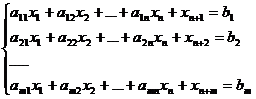
 с базисом Б = (An+1,An+2,…,An+m) (в этом случае исходный базис целиком состоит из искусственных векторов).
с базисом Б = (An+1,An+2,…,An+m) (в этом случае исходный базис целиком состоит из искусственных векторов).





 Матрица упрощается след. Образом: Вычеркиваются строки, каждый элемент такой строки меньше или равен элементу другой строки).Вычеркиваются столбцы, каждый элемент которого больше или равен элементу другого столбца. Упрощая платежную матрицу, мы приходим в состояние, когда у одного из игроков остается только две стратегии. Тогда возможно решить игру графическим способом.
Матрица упрощается след. Образом: Вычеркиваются строки, каждый элемент такой строки меньше или равен элементу другой строки).Вычеркиваются столбцы, каждый элемент которого больше или равен элементу другого столбца. Упрощая платежную матрицу, мы приходим в состояние, когда у одного из игроков остается только две стратегии. Тогда возможно решить игру графическим способом.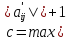 (
(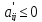 ).
).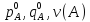 .
.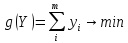
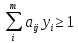
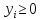
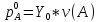 , если
, если 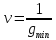
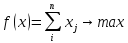
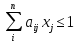
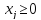
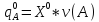 , если
, если 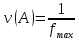
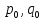 совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.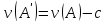 .
.


