ДАЛЬШЕ НЕОБЯЗАТЕЛЬНО
Для решения задачи линейного программирования её нужно записать в приведенной канонической форме, в некоторых ситуациях – в стандартной. Поэтому возникает потребность переходить от одной формы задачи к другим:
1. Задачу на минимум переписать в задачу на максимум, домножив целевую функцию на -1.
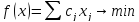 .
.
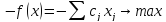 .
.
2. Стандартная форма требует ограничений в сторону меньше, но имеется одно из ограничений в сторону больше. Необходимо домножить это ограничение на -1.
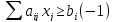
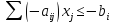
3. Если ограничения заданы в виде равенств, нужна стандартная форма, то их можно расписать в виде системы двух неравенств:
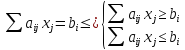 . Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше:
. Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше: 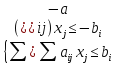 .
.
4. Если величина 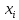 любого знака, а для стандартной формы требуется неотрицательная величина, то необходимоxпредставить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения:
любого знака, а для стандартной формы требуется неотрицательная величина, то необходимоxпредставить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения: 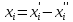 .
.
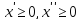 .
.
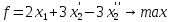
5. Требуется перейти из неравенства в равенство.
При приведении к канонической форме нужно вводить дополнительные (балансовые) переменные. В каждое ограничение записывается своя балансовая переменная, соответственно их столько же, сколько ограничений. Балансовые переменные обязательно неотрицательные.
С их помощью можно уравнять как ограничение в сторону меньше, так и ограничения в сторону больше. В первом случае балансовая переменная прибавляются к ограничению, во втором – отнимается.
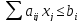 ;
;
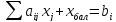 .
.
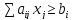 ;
;
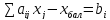 .
.
Балансовые переменные записываются в целевую функцию с нулевым коэффициентом. Добавление балансовой переменной не влияет на значение х.
6. Иногда встречаются задачи, в которых добавляется какой-то числовой коэффициент c. Тогда решаем с переменными, а потом добавим это число с. То есть нужно перейти к функции, которая меньше на это число с, решить задачу и прибавить к ответу это число.
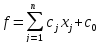 .
.
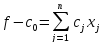 .
.
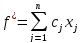 .
.
Определения допустимого, опорного (базисного), оптимального решений ЗЛП. Основная теорема ЛП.
При решении задач линейного программирования бывают:
1. Допустимые решения (допустимый план) – такой набор 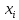 , который удовлетворяет системе ограничений.
, который удовлетворяет системе ограничений.
2. Базисное решение (план) – допустимое решение, в котором все свободные переменные равны нулю, а все базисные неотрицательные (т.е. задача в канон форме). Всегда достигается в вершинах области.
3. Оптимальное решение (план) – решение, на котором функция достигает своего оптимального значения (т.е. максимума или минимума, в зависимости от условия задачи). Оптимальное решение также является допустимым. Оптимальное решение всегда базисное.
Симплексный метод. Приведение ЗЛП к канонической форме. Дополнительные переменные. Выбор разрешающего элемента. (Признак неоптимального базисного решения / Признак неограниченного значения целевой функции/ Признак альтернативного рещения)
Стандартной задачей ЛП называется задача на максимум вида:
В этой задаче ищется максимум целевой функции при условии неотрицательности всех переменных и ограничений в виде неравенств со знаком. В матрично-векторной форме ограничения стандартной задачи выглядят следующим образом:
Здесь-план,-матрица системы ограничений размера,- вектор правых частей ограничений. Если правые части ограничений неотрицательные, то множество допустимых планов непустое. Если условие неотрицательности правых частей не выполняется, то множество допустимых планов может оказаться пустым.
Канонической называется задача вида:
где ранг матрицы A равен m (числу ее строк). В отличие от стандартной задачи в канонической задаче все ограничения являются уравнениями, а знаки правых частей уравнений могут быть произвольными. Для получения опорных планов задачи ЛП в канонической форме выбирается любой набор из m столбцов матрицы, образующих линейно независимую систему. Переменные, соответствующие этим столбцам, называются базисными. Решение уравнения, в котором все свободные переменные равны нулю, называется базисным решением. Допустимое базисное решение системы ограничений называется базисным планом задачи. Базисный план, содержащий точно нулевых компонент, называется невырожденным. Если нулевых компонент больше, то план вырожденный. Базис, соответствующий оптимальному плану задачи, называется оптимальным базисом.
Общая задача ЛП может быть приведена к специальным формам:
1) Задача на минимум (максимум) преобразуется в задачу на максимум (минимум) введением новой целевой функции,
2) Преобразование позволяет избавиться от коэффициента в целевой функции
3) Умножение неравенства на минус
4) Ограничение в виде уравнения эквивалентно системе из двух ограничений с противоположными знаками
5) Любое неравенство можно превратить в уравнение с помощью дополнительных (балансовых) неотрицательных переменных
В целевую функцию преобразованной задачи дополнительные переменные вводятся с нулевыми коэффициентами.
(a) Признак оптимального базисного решения. Признак единственного оптимального решения.
Если все оценки базисного плана неотрицательные, то базисный план является оптимальным. Положительность всех оценок свободных переменных оптимального плана свидетельствует о единственности оптимального плана.
Единственность оптимальное решение
| Базисные переменные
| положительны, либо равны нулю
|
| Оценки базисных переменных
| равны нулю
|
| Свободные переменные
| равны нулю
|
| Оценки свободных переменных
| положительны
|
(b) Признак неоптимального базисного решения.
Наличие отрицательной оценки требует продолжения исследования.
(Есть отрицательные оценки, можно выбрать разрешающую строку.)
(c) Признак неограниченного значения целевой функции.
Если среди столбцов, отвечающих отрицательным оценкам свободных переменных базисного плана, имеется столбец с неположительными элементами, то задача ЛП не имеет решения из-за неограниченного возрастания целевой функции на множестве допустимых планов.
(d) Признак альтернативного решения.
Если в оптимальном плане все оценки свободных переменных строго положительные, то оптимальный план единственный. Если есть нулевые оценки свободных переменных, а план невырожденный, то имеются альтернативные оптимальные планы. В случае вырожденного плана и наличия нулевых оценок требуется дополнительное исследование.
Для вычисления альтернативных оптимальных планов в качестве разрешающего выбирается столбец с нулевой оценкой свободной переменой. Если среди его элементов имеется положительный элемент, то переход к новой таблице приведет к другому оптимальному плану. При этом множество оптимальных планов заведомо содержит ребро, соединяющее два найденных плана. Если среди та- ких столбцов найдется столбец, все элементы которого неположительные, то множество оптимальных планов будет содержать бесконечное ребро. Одновременно неограниченным будет и множество оптимальных планов.
Альтернативное решение
| Базисные переменные
| положительны, либо равны нулю
|
| Оценки базисных переменных
| равны нулю
|
| Свободные переменные
| равны нулю
|
| Оценки свободных переменных
| какая-то оценка свободной переменной равна нулю
|
Чтобы найти альтернативное решение нужно свободную переменную, которая равна 0, сделать базисной, выбрав ее столбец в качестве разрешающего, и пересчитать таблицу как обычно.
Вырожденное решение:
| Базисные переменные
| какая-то базисная переменная равна нулю
|
| Оценки базисных переменных
| равны нулю
|
| Свободные переменные
| равны нулю
|
| Оценки свободных переменных
| положительны
|
Вырожденное решение может быть и единственным.
Задача, двойственная данной
Задача, двойственная данной, строится по определению следующим образом:
Если прямая задача на максимум, то двойственная – на минимум.
Если задача на максимум, то ограничения либо в сторону меньше, либо равенства. Соответственно и наоборот: если задача на минимум, то ограничения в сторону больше, либо равенства.
Число переменных двойственной задачи равняется числу ограничений прямой.
Число ограничений двойственной задачи равняется числу переменных прямой.
Матрицы ограничений прямой и двойственной задачи транспонированы относительно друг друга.
Чтобы составить двойственную задачу каждому ограничению прямой задачи сопоставляют переменную двойственной.
Коэффициент целевой функции двойственной задачи равен правым частям ограничений прямой задачи (.
Правые части ограничений двойственной задачи совпадают с коэффициентами целевой функции прямой задачи.
Если ограничение задано в виде неравенства, то двойственная переменная неотрицательна.
Если ограничение задано в виде равенства, то двойственная переменная может принимать любые значения.
Если переменная прямой задачи неотрицательна, то ограничение двойственной заданы в виде неравенства.
Если переменная прямой задачи может принимать любые значения, то соответствующее ограничение двойственной задано в виде равенства.
Задача, двойственная двойственной, является прямой.
26. Связь решения матричной игры с задачей ЛП для первого (второго) игрока
Задачу антагонистической игры можно свести к двум взаимнодвойственным задачам линейного программирования
Пусть дана игровая матрица А’, для которой существуют элементы меньшие или равные нулю.
Нужно перейти к матрице А=А’+сS, где 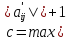 (
(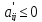 ).
).
Получаем новую матрицу, в которой все элементы уже положительны. Чтобы решить игру нужно найти 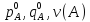 .
.
Для матрицы А нужно составить пару взаимнодвойственных задач:
| Прямая
| Двойственная
|
Y-?
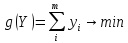
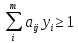
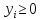
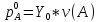 , если , если 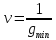
| X-?
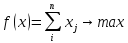
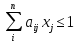
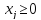
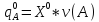 , если , если 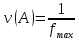
|
Оптимальный вектор для матрицы А равен оптимальному вектору для матрицы А’ (т.е. оптимальные стратегии 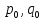 совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
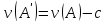 .
.
Плоские графы
Граф называется плоским (планарным), если его можно уложить на плоскости так, чтобы его ребра нигде не пересекались, кроме как в вершинах.
2) Двудольный граф
Двудольный граф (или биграф, или чётный граф) — это граф G(V,E), такой что множество вершин V разбито на два непересекающихся подмножества V1 и V2, причём всякое ребро E инцидентно вершине из V1 и вершине из V2 (то есть соединяет вершину из V1 с вершиной из V2).
Псевдограф
Псевдограф – граф с кратными ребрами и петлями.
4) Полный граф
Полный граф — простой граф, в котором каждая пара различных вершин смежна
ДАЛЬШЕ НЕОБЯЗАТЕЛЬНО
Для решения задачи линейного программирования её нужно записать в приведенной канонической форме, в некоторых ситуациях – в стандартной. Поэтому возникает потребность переходить от одной формы задачи к другим:
1. Задачу на минимум переписать в задачу на максимум, домножив целевую функцию на -1.
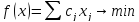 .
.
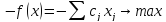 .
.
2. Стандартная форма требует ограничений в сторону меньше, но имеется одно из ограничений в сторону больше. Необходимо домножить это ограничение на -1.
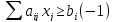
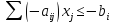
3. Если ограничения заданы в виде равенств, нужна стандартная форма, то их можно расписать в виде системы двух неравенств:
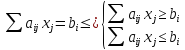 . Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше:
. Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше: 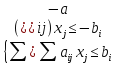 .
.
4. Если величина 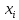 любого знака, а для стандартной формы требуется неотрицательная величина, то необходимоxпредставить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения:
любого знака, а для стандартной формы требуется неотрицательная величина, то необходимоxпредставить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения: 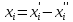 .
.
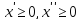 .
.
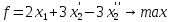
5. Требуется перейти из неравенства в равенство.
При приведении к канонической форме нужно вводить дополнительные (балансовые) переменные. В каждое ограничение записывается своя балансовая переменная, соответственно их столько же, сколько ограничений. Балансовые переменные обязательно неотрицательные.
С их помощью можно уравнять как ограничение в сторону меньше, так и ограничения в сторону больше. В первом случае балансовая переменная прибавляются к ограничению, во втором – отнимается.
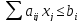 ;
;
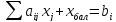 .
.
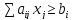 ;
;
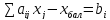 .
.
Балансовые переменные записываются в целевую функцию с нулевым коэффициентом. Добавление балансовой переменной не влияет на значение х.
6. Иногда встречаются задачи, в которых добавляется какой-то числовой коэффициент c. Тогда решаем с переменными, а потом добавим это число с. То есть нужно перейти к функции, которая меньше на это число с, решить задачу и прибавить к ответу это число.
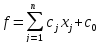 .
.
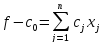 .
.
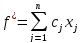 .
.
Постановка транспортной задачи. Необходимое и достаточное условие существования допустимого решения транспортной задачи.
Введем некоторые обозначения: ПОi – пункты отправления груза; ПНj – пункты назначения; ai– количество груза, имеющееся в ПОi; bj– количество груза, которое требуется ПНj; сij– тариф (стоимость перевозки единицы груза из ПО в ПН); хij– количество груза, перевозимое из ПО в ПН.
В общем виде транспортная задача задается так:
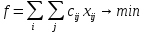 (нам нужно перевести груз с минимальными затратами, поэтому задача на минимум).
(нам нужно перевести груз с минимальными затратами, поэтому задача на минимум).
Ограничения: 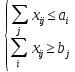
Чтобы все ПО были вывезены, а все потребности ПН были удовлетворены, ограничения задаются в виде равенств. При этом если количество груза во всех ПО совпадает с количеством груза, которое требуется всем ПН, то задача является уравновешенной (сбалансированной).
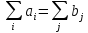 – условие равновесия (груз во всех ПО=потребностям всех ПН).
– условие равновесия (груз во всех ПО=потребностям всех ПН).
Для того, чтобы транспортная задача имела решение, необходимо и достаточно, чтобы выполнялось условие баланса (равновесия).
Необходимо: Дано: задача имеет решение. Доказать: выполняется условие равновесия.
Доказательство: Если задача имеет решение, то существует такой Х, что выполняются ограничения:

Просуммируем первое ограничение по строкам (сумма по i), второе по столбцам (сумма поj).
Получим:
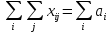 .
. 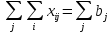 .
.
Во втором уравнении поменяем местами сумму по iипоj. Тогда левые части двух уравнений будут одинаковы, а следовательно и правые части равны между собой: 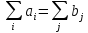
Достаточно: Дано: выполняется условие равновесия.
Доказать: задача имеет решение.
В качестве 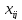 возьмем выражение
возьмем выражение 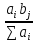 .
.
Подставим в первое ограничение и вынесем аi за скобку:
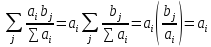 .
.
Выражение в скобке равно единице, так как выполняется условие равновесия.
Подставим во второе ограничение:
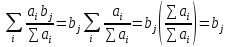 .
.
Таким образом, сбалансированная (уравновешенная) транспортная задача всегда имеет решение.
Определения допустимого, опорного (базисного), оптимального решений ЗЛП. Основная теорема ЛП.
При решении задач линейного программирования бывают:
1. Допустимые решения (допустимый план) – такой набор 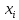 , который удовлетворяет системе ограничений.
, который удовлетворяет системе ограничений.
2. Базисное решение (план) – допустимое решение, в котором все свободные переменные равны нулю, а все базисные неотрицательные (т.е. задача в канон форме). Всегда достигается в вершинах области.
3. Оптимальное решение (план) – решение, на котором функция достигает своего оптимального значения (т.е. максимума или минимума, в зависимости от условия задачи). Оптимальное решение также является допустимым. Оптимальное решение всегда базисное.



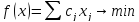 .
.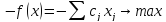 .
.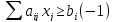
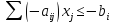
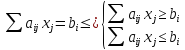 . Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше:
. Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше: 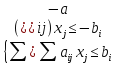 .
.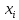 любого знака, а для стандартной формы требуется неотрицательная величина, то необходимоxпредставить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения:
любого знака, а для стандартной формы требуется неотрицательная величина, то необходимоxпредставить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения: 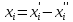 .
.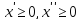 .
.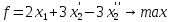
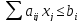 ;
;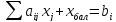 .
.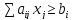 ;
;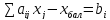 .
.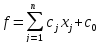 .
.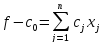 .
.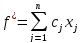 .
.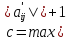 (
(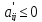 ).
).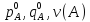 .
.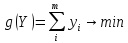
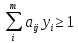
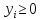
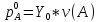 , если
, если 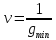
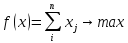
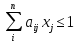
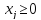
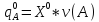 , если
, если 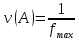
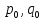 совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.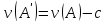 .
.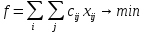 (нам нужно перевести груз с минимальными затратами, поэтому задача на минимум).
(нам нужно перевести груз с минимальными затратами, поэтому задача на минимум).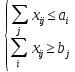
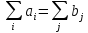 – условие равновесия (груз во всех ПО=потребностям всех ПН).
– условие равновесия (груз во всех ПО=потребностям всех ПН).
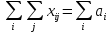 .
. 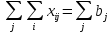 .
.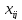 возьмем выражение
возьмем выражение 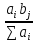 .
.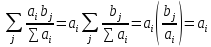 .
.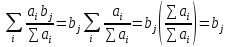 .
.


