Если фигура ограничена кривой, заданной параметрическими уравнениями, то площадь вычисляется по формуле:
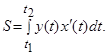
Пример. Вычислить площадь эллипса, заданного параметрическими уравнениями: 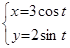 .
.
Решение. Дан эллипс с полуосями: большая — 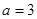 , малая —
, малая — 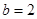 . Сделаем чертеж к задаче (рис.4).
. Сделаем чертеж к задаче (рис.4).
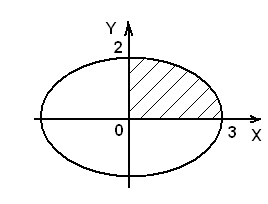
Рис. 4
В силу симметричности фигуры вычислим 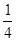 площади. Найдем пределы интегрирования:
площади. Найдем пределы интегрирования:
так как  , то
, то 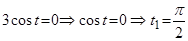 ;
;
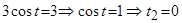 .
.
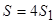 .
.
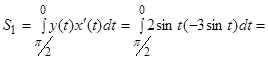
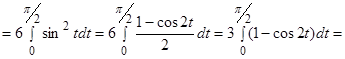
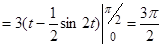 .
.
Следовательно, площадь 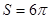 (кв.ед.).
(кв.ед.).
Задание 12. Вычисление площади плоской фигуры, ограниченной линиями, заданными в полярных координатах.
В полярной системе координат элементарной фигурой является криволинейный сектор (рис.5), площадь которого вычисляется по формуле:
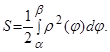
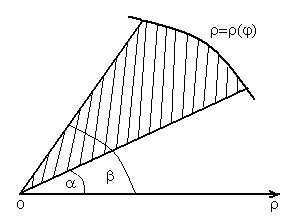
Рис. 5
Пример. Найти площадь фигуры, ограниченной линией 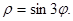
Решение. Так как 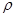 определяет расстояние до соответствующей точки, то
определяет расстояние до соответствующей точки, то 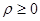 . Следовательно, область определения функции определяется неравенством
. Следовательно, область определения функции определяется неравенством 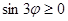 . Общее решение этого неравенства имеет вид:
. Общее решение этого неравенства имеет вид:
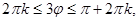 где
где 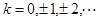 .
.
Отсюда 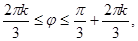
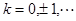 . Так как в полярной системе координат выполняются ограничения на область изменения
. Так как в полярной системе координат выполняются ограничения на область изменения 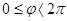 , то область допустимых значений функции
, то область допустимых значений функции 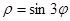 в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами:
в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами:
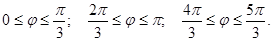
Выбрав несколько значений 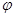 из указанных промежутков, построим график функции (рис. 6).
из указанных промежутков, построим график функции (рис. 6).
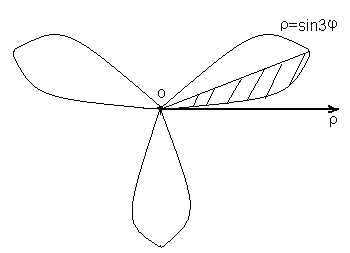
Рис.6
В силу симметричности фигуры вычислим 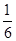 площади, где полярный угол
площади, где полярный угол 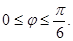
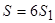 .
.
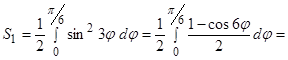
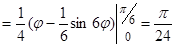 .
.
Следовательно, площадь всей фигуры 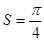 (кв.ед.).
(кв.ед.).
Задание 13. Вычисление длины дуги кривой, заданной параметрическими уравнениями.
Длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле:
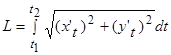 .
.
Замечание. При вычислении длины кривой, заданной параметрическими уравнениями, нижний предел интегрирования должен быть меньше верхнего предела интегрирования.
Пример. Вычислить длину дуги астроиды, заданной уравнениями:
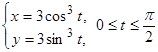 .
.
Решение.
Вычислим производные функций:
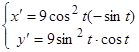 .
.
Вычислим подынтегральную функцию:
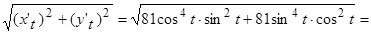
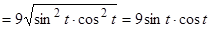 .
.
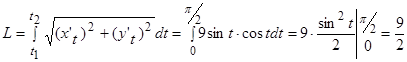 .
.
Следовательно, длина дуги 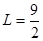 (ед.).
(ед.).
Задание 14. Вычисление объема тела, образованного вращением фигуры, ограниченной линиями в декартовых координатах.
Пусть дана криволинейная трапеция, ограниченная линиями 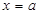 ,
, 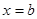 ,
, 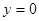 ,
, 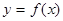 , где
, где  - непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле:
- непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле:
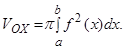
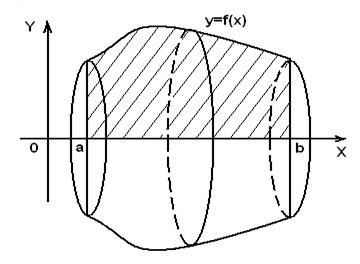
Рис.7
Если криволинейную трапецию, ограниченную линиями 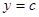 ,
, 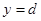 ,
,  ,
,  , где
, где 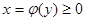 - непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле:
- непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле:
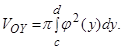
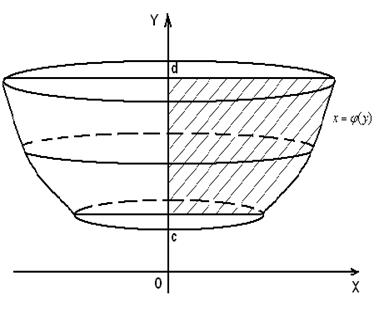
Рис.8
Пусть дана криволинейная трапеция, ограниченная линиями 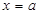 ,
, 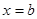 ,
, 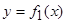 ,
, 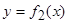 , где
, где 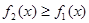 (рис.9), то объем полученного тела вращения вычисляется по формуле:
(рис.9), то объем полученного тела вращения вычисляется по формуле:
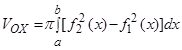 .
.
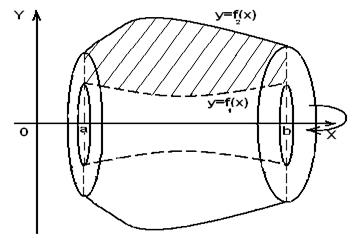
Рис.9
Пример. Криволинейная трапеция, ограниченная осью абсцисс и кривой 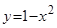 вращается вокруг оси
вращается вокруг оси  . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
Решение. На рис.10 изображена криволинейная трапеция, которая вращается вокруг оси  .
.
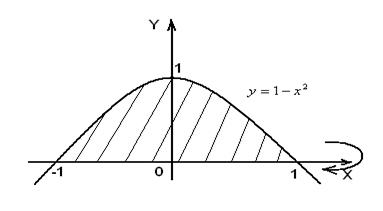
Рис.10
Точки пересечения кривой 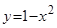 с осью
с осью 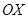 :
: 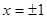 .
.
Следовательно, пределы интегрирования: 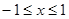 .
.
Искомый объем тела вращения:
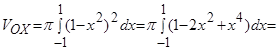
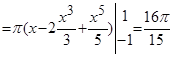 (куб.ед.).
(куб.ед.).
Пример. Криволинейная трапеция, ограниченная осью ординат и кривой 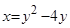 вращается вокруг оси
вращается вокруг оси 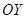 . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
Решение. На рис.11 изображена криволинейная трапеция, которая вращается вокруг оси 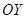 .
.
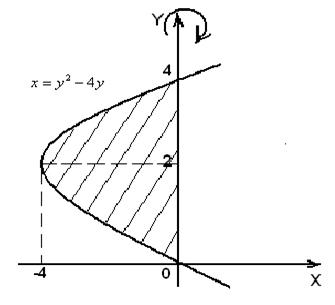
Рис.11
Кривая 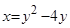 — это парабола с вершиной (-4;2), которая пересекает ось ординат в точках
— это парабола с вершиной (-4;2), которая пересекает ось ординат в точках 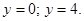
Следовательно, пределы интегрирования: 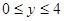 .
.
Искомый объем тела вращения:
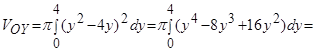
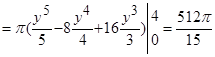 (куб. ед.).
(куб. ед.).
Пример. Фигура, ограниченная линиями 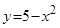 и
и 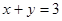 ,вращается вокруг
,вращается вокруг  . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
Решение. На рис.12 изображена фигура, которая вращается вокруг оси  .
.
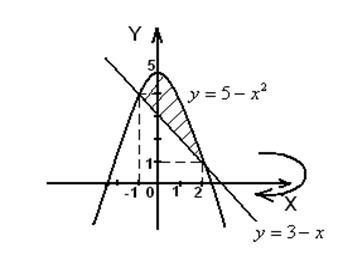
Рис.12
Точки пересечения параболы 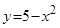 и прямой
и прямой 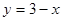
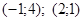 .
.
Следовательно, пределы интегрирования: 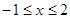 .
.
Искомый объем тела вращения вычислим по формуле:
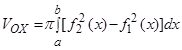 .
.
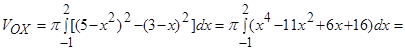
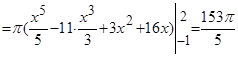 (куб. ед.).
(куб. ед.).



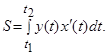
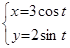 .
.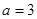 , малая —
, малая — 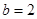 . Сделаем чертеж к задаче (рис.4).
. Сделаем чертеж к задаче (рис.4).
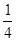 площади. Найдем пределы интегрирования:
площади. Найдем пределы интегрирования: , то
, то 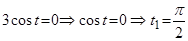 ;
;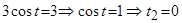 .
.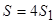 .
.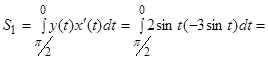
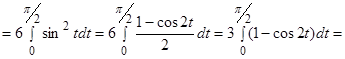
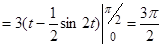 .
.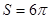 (кв.ед.).
(кв.ед.).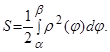

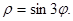
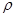 определяет расстояние до соответствующей точки, то
определяет расстояние до соответствующей точки, то 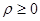 . Следовательно, область определения функции определяется неравенством
. Следовательно, область определения функции определяется неравенством 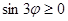 . Общее решение этого неравенства имеет вид:
. Общее решение этого неравенства имеет вид: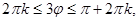 где
где 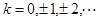 .
.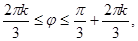
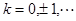 . Так как в полярной системе координат выполняются ограничения на область изменения
. Так как в полярной системе координат выполняются ограничения на область изменения 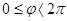 , то область допустимых значений функции
, то область допустимых значений функции 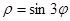 в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами:
в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами: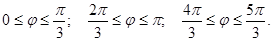
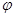 из указанных промежутков, построим график функции (рис. 6).
из указанных промежутков, построим график функции (рис. 6).
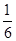 площади, где полярный угол
площади, где полярный угол 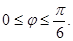
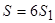 .
.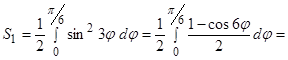
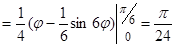 .
.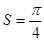 (кв.ед.).
(кв.ед.).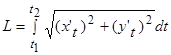 .
.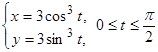 .
.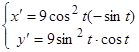 .
.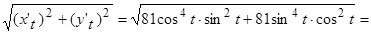
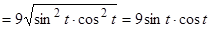 .
.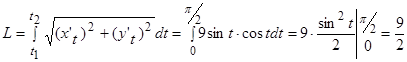 .
.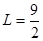 (ед.).
(ед.).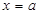 ,
, 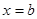 ,
, 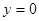 ,
, 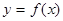 , где
, где  - непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле:
- непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле: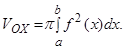

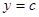 ,
, 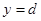 ,
,  ,
,  , где
, где 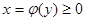 - непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле:
- непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле: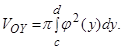

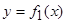 ,
, 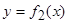 , где
, где 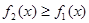 (рис.9), то объем полученного тела вращения вычисляется по формуле:
(рис.9), то объем полученного тела вращения вычисляется по формуле: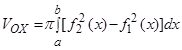 .
.
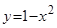 вращается вокруг оси
вращается вокруг оси 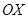 . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
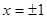 .
.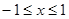 .
.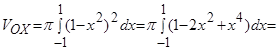
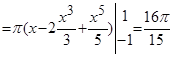 (куб.ед.).
(куб.ед.).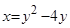 вращается вокруг оси
вращается вокруг оси 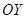 . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
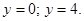
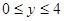 .
.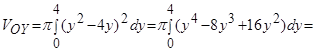
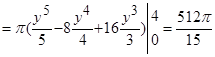 (куб. ед.).
(куб. ед.).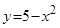 и
и 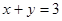 ,вращается вокруг
,вращается вокруг 
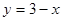
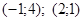 .
.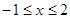 .
.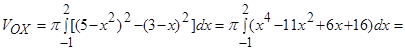
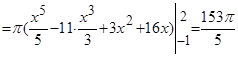 (куб. ед.).
(куб. ед.).

