Определение. Случайная величина, принимающая несчетное число значений (значения которой заполняют некоторый промежуток) и имеющая плотность, называется случайной величиной с абсолютно непрерывным законом распределения или (абсолютно) непрерывной случайной величиной..
В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полубесконечными или бесконечными, например: (a; b ], (–µ; a), [ b;µ), (–µ; µ).
При описании непрерывной случайной величины невозможно выписать и пронумеровать все её значения, принадлежащие даже достаточно узкому интервалу. Эти значения образуют несчётное множество.
Замечание. Вернемся к нашей аналогии со стержнем. Теперь на нем не точечные массы, а сам он представляет собой стержень переменной плотности, протянувшийся от наименьшего до наибольшего значения случайной величины. Очевидно, что вопрос о массе в конкретной точке теперь невозможно поставить, а можно лишь говорить о массе, распределенной в некотором объеме (на некотором участке нашего стержня).
Таким образом, вместо вероятности-массы мы получаем плотность (вероятности). Из-за схожести физической и вероятностной плотности последнюю чаще всего обозначают, как в физике, буквой ρ (греческая ро). Другой распространенный вариант – р – подчеркивает связь с вероятностью.
Замечание. Если Х – непрерывная случайная величина, то равенство Х = х представляет собой, как и в случае дискретной случайной величины, некоторое случайное событие, но для непрерывной случайной величины это событие можно связать лишь с вероятностью, равной нулю, что, однако, не влечёт за собой невозможности события. Поэтому, применительно к абсолютно непрерывным случайным величинам, говорят только о вероятности попасть в промежуток.
Пусть Х – непрерывная случайная величина. Рассмотрим для некоторого числа х вероятность неравенства х < Х < х + D х
P (х < Х < х + D х).
Здесь D х – величина малого интервала.
Очевидно, что если D х ® 0, то P (х < Х < х + D х)® 0. Обозначим r(х) предел отношения P (х < Х < х + D х) к при D х ® 0, если такой предел существует:
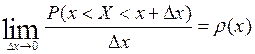
Функция r(х) называется плотностью распределения случайной величины. Из этой формулы следует равенство, справедливое для малых величин D х, которое также можно считать определением функции r(х):
P (х < Х < х + D х)  r(x)D х
r(x)D х
Очевидно, что r(x) – неотрицательная функция. Для определения вероятности того, что случайная величина Х примет значение из промежутка [ a, b ] конечной длины, нужно выбрать на промежутке произвольные числа x 1, х 2,¼, хn удовлетворяющие условию а=х 0< х 1< x 2<¼< xn < b=xn+ 1. Эти числа разобьют промежуток [ a, b ] на n +1 частей, представляющих собой промежутки [ х 0, х 1), [ х 1, х 2), ¼,[ хn, b ]. Введём обозначения:
D х 0= х 1 – х 0, D х 1= х 2 – х 1, ¼, D хn = b – хn,
и составим сумму  . Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина D хi стремится к нулю. Будем считать функцию r (x) непрерывной на промежутке (а; b), тогда пределом суммы
. Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина D хi стремится к нулю. Будем считать функцию r (x) непрерывной на промежутке (а; b), тогда пределом суммы 
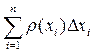 будет определённый интеграл по промежутку [ a; b ] от функции p (x), равный искомой вероятности:
будет определённый интеграл по промежутку [ a; b ] от функции p (x), равный искомой вероятности:
P (a £ Х £ b) =  (3)
(3)
 Замечание
Замечание. Это равенство можно также рассматривать как определение функции r (
х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (
х 1,
х 2) равна площади фигуры, образованной отрезком [
х 1,
х 2] оси
х,графиком функции r(
х) и вертикальными прямыми
х =
х 1,
х = х 2, как изображено на рисунке 1.
Замечание. С другой стороны, вероятность попасть в промежуток есть разность значений функции распределения на концах промежутка.
Если все возможные значения случайной величины принадлежат интервалу (а; b), то для r (х) – её плотности распределения справедливо равенство
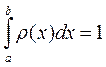
Для удобства иногда считают функцию r(х) определённой для всех значений х, полагая её равной нулю в тех точках х, которые не являются возможными значениями этой случайной величины.
Плотностью распределения может служить любая интегрируемая функция r(х), удовлетворяющая двум условиям:
1) r(х) ³ 0;
2) 
Определение. Законом распределения непрерывной случайной величины является ее плотность.
Можно задавать случайную величину, задавая функцию r(х), удовлетворяющую этим условиям.
В качестве примера рассмотрим случайную величину Х, равномерно распределённую на промежутке [ a; b ]. В этом случае r(х) постоянна внутри этого промежутка:

По свойству 2) функции r (х)
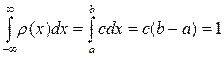

 Отсюда
Отсюда  . График функции
. График функции
r (х) представлен на рисунке 2.
Замечанание. Во многих практических задачах встречаются случайные величины, у которых возможные значения не ограничены сверху и снизу. В этом случае кривая распределения располагается над осью х и при х ® ¥ и х ® – ¥ асимптотически приближается к этой оси, как изображено на рисунке 1. Вероятность того, что случайная величина Х примет значение, меньшее некоторого числа а, равна площади фигуры, заключённой между кривой распределения и горизонтальной координатной осью слева от точки а. Будем считать, что такая площадь существует.
Напоминание. Пусть Х – непрерывная случайная величина. Функция F (x), которая определяется равенством
 ,
,
называется интегральной функцией распределения или просто функцией распределения случайной величины Х. Непосредственно из определения следует равенство  . Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению
. Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению  . Плотность распределения r (х) называют еще дифференциальной функцией распределения.
. Плотность распределения r (х) называют еще дифференциальной функцией распределения.
Замечание. Определение. Иногда плотность (закон распределения) определяют «в обратную сторону»: Плотность есть подинтегральная функция функции распределения абсолютно непрерывной случайной величины.
 .
.
Замечание. Таким образом, если известна плотность распределения случайной величины, для нахождения функции распределения необходимо взять от нее указанный выше интеграл, а если, наоборот, известна функция распределения, то плотность находится дифференцированием (взятием производной) этой функции.
Нахождение неизвестного параметра плотности находится с помощью свойства 2) – равенства 1 интеграла от плотности по всей числовой оси.
Например, если на всей оси Х r(х) = 2С / (1 + x2) Найти С. Рассмотрев интеграл от r по всей оси, получим С = 1/2p
Отступление.



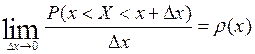
 r(x)D х
r(x)D х . Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина D хi стремится к нулю. Будем считать функцию r (x) непрерывной на промежутке (а; b), тогда пределом суммы
. Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина D хi стремится к нулю. Будем считать функцию r (x) непрерывной на промежутке (а; b), тогда пределом суммы 
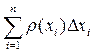 будет определённый интеграл по промежутку [ a; b ] от функции p (x), равный искомой вероятности:
будет определённый интеграл по промежутку [ a; b ] от функции p (x), равный искомой вероятности: (3)
(3) Замечание. Это равенство можно также рассматривать как определение функции r (х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (х 1, х 2) равна площади фигуры, образованной отрезком [ х 1, х 2] оси х,графиком функции r(х) и вертикальными прямыми х = х 1, х = х 2, как изображено на рисунке 1.
Замечание. Это равенство можно также рассматривать как определение функции r (х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (х 1, х 2) равна площади фигуры, образованной отрезком [ х 1, х 2] оси х,графиком функции r(х) и вертикальными прямыми х = х 1, х = х 2, как изображено на рисунке 1.
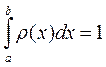


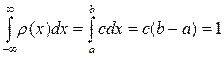

 Отсюда
Отсюда  . График функции
. График функции ,
, . Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению
. Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению  . Плотность распределения r (х) называют еще дифференциальной функцией распределения.
. Плотность распределения r (х) называют еще дифференциальной функцией распределения.


