И практической деятельности широко используются дроби, знаменатели которых являются степенями 10. Их называют десятичными.
Определение. Десятичной называется дробь вида 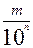 , где m и n- натуральные числа.
, где m и n- натуральные числа.
Десятичные дроби принято записывать без знаменателя. Например, дробь  записывают в виде 3,67, а дробь
записывают в виде 3,67, а дробь  в виде 0,007.
в виде 0,007.
Выясним, как образуется такая запись.
Пусть дана дробь 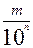 , где m, n
, где m, n  N. Представим ее числитель в следующем виде:
N. Представим ее числитель в следующем виде:
m = аk·10k+аk-1·10k-1+…+а1·10+а0.
Тогда, по правилам действий над степенями при n < k, получим:
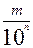 =
= 
=аk·10k-n+аk-1·10k-n-1+…+аn+ 
Сумма аk·10k-n+…+аn является записью целого неотрицательного числа (обозначим его буквой А), а сумма  представляет дробную часть числа, ее принято записывать без знаменателя в виде
представляет дробную часть числа, ее принято записывать без знаменателя в виде  . Таким образом,
. Таким образом,
дробь 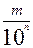 можно представить в следующем виде:
можно представить в следующем виде:  , т.е. при записи дроби
, т.е. при записи дроби  последние n цифр десятичной записи числа т отделяют запятой. Если числитель содержит менее чем n десятичных знаков, то перед ним пишут столько нулей, чтобы получилась n + 1 цифра, после чего отделяют запятой n знаков, начиная с конца. Например,
последние n цифр десятичной записи числа т отделяют запятой. Если числитель содержит менее чем n десятичных знаков, то перед ним пишут столько нулей, чтобы получилась n + 1 цифра, после чего отделяют запятой n знаков, начиная с конца. Например,  0,0047.
0,0047.
Как известно, сравнение десятичных дробей и арифметические действия над ними легко выполнять, если дроби имеют один и тот же знаменатель.
В основе приведения десятичных дробей к общему знаменателю лежит следующее утверждение: если к десятичной дроби  приписать справа любое число нулей, то получится десятичная дробь, равная данной.
приписать справа любое число нулей, то получится десятичная дробь, равная данной.
Это свойство позволяет приводить десятичные дроби к общему знаменателю следующим образом: если у одной дроби после запятой стоит n цифр, а у другой р цифр, причем n < р, то для приведения их к общему знаменателю достаточно к первой дроби приписать справа р - n нулей. Тогда у обеих дробей после запятой будет стоять поровну цифр, а это значит, что они имеют один и тот же знаменатель.
Пользуясь этим правилом, легко выполнять сравнение десятичных дробей, так как оно сводится к сравнению натуральных чисел: чтобы сравнить две десятичные дроби, надо уравнять в них число десятичных знаков после запятой, отбросить запятые и сравнить получившиеся натуральные числа.
Например, 4,62517 > 4,623, так как 4,623 = 4,62300, а 4,62517 > 4,62300, так как 462517 > 462300.
Как известно, для дробей, имеющих одинаковые знаменатели, сложение и вычитание сводится к соответствующим операциям над их числителями. Это позволяет свести сложение и вычитание десятичных дробей к действиям над натуральными числами.
Например, 2,54+3,7126=2,5400+3,7126=  +
+  +
+  =6,2526.
=6,2526.
Умножение и деление десятичных дробей не требует приведения их к общему знаменателю, но они также сводятся к соответствующим действиям над натуральными числами.
Среди десятичных дробей выделяют и часто используют дробь 0,01. Ее называют процентом и обозначают 1%. Запись р% обозначает  . Например, 25%- это дробь
. Например, 25%- это дробь  , или 0,25.
, или 0,25.
Проценты были введены, когда не существовало десятичных дробей. Чтобы производить расчеты по займам, определяли прирост капитала из расчета 100 денежных единиц. Этот прирост и называли числом процентов (pro centum - на сто).
Простота сравнения и выполнения действий над десятичными дробями приводит к следующему вопросу: любую ли дробь вида  (m, n
(m, n  N) можно записать в виде конечной десятичной дроби, т.е. дроби, у которой после запятой стоит конечное число цифр? Ответ на него дает следующая теорема.
N) можно записать в виде конечной десятичной дроби, т.е. дроби, у которой после запятой стоит конечное число цифр? Ответ на него дает следующая теорема.
Теорема. Для того чтобы несократимая дробь  была равна десятичной, необходимо и достаточно, чтобы в разложение ее знаменателя n на простые множители входили лишь простые числа 2 и 5.
была равна десятичной, необходимо и достаточно, чтобы в разложение ее знаменателя n на простые множители входили лишь простые числа 2 и 5.
Так, например, дробь — можно записать в виде десятичной: она несократима и 80 = 24·5. Дробь — несократима, но 15 = 3·5. Поскольку в разложение знаменателя этой дроби входит множитель, отличный от 2 и 5, то дробь  нельзя записать в виде десятичной.
нельзя записать в виде десятичной.

 Дробь
Дробь  нельзя представить в виде конечной десятичной дроби. Но, деля 1 на 3, получаем, что 0,3 <
нельзя представить в виде конечной десятичной дроби. Но, деля 1 на 3, получаем, что 0,3 <  < 0,4. Далее находим, что 0,33 <
< 0,4. Далее находим, что 0,33 <  < 0,34; 0,333 <
< 0,34; 0,333 <  < 0,334 и т.д. Вообще для любого n имеем: 0,3…33 <
< 0,334 и т.д. Вообще для любого n имеем: 0,3…33 <  < 0,334.
< 0,334.
n цифр n цифр
Вместо того чтобы писать бесконечное множество неравенств, говорят, что дроби  соответствует бесконечная десятичная дробь 0,33...3.... Это означает, что если отбросить в бесконечной дроби все цифры, начиная с некоторой, то будем иметь число, меньшее
соответствует бесконечная десятичная дробь 0,33...3.... Это означает, что если отбросить в бесконечной дроби все цифры, начиная с некоторой, то будем иметь число, меньшее  , а если в полученном числе увеличить
, а если в полученном числе увеличить
последнюю цифру на 1, то будет число, большее  .
.
Любую конечную десятичную дробь можно записать в виде бесконечной, приписав к ней справа последовательность нулей. Например, дробь 0,25 можно записать так: 0,25000...0.... Здесь для всех цифр, начиная с некоторой, получится число, не превосходящее 0,25 (например, если оставить лишь одну цифру после запятой, то получится 0,2, меньше 0,25, а если оставить три цифры после запятой, то будет число 0,250, равное 0,25). Если же после отбрасывания увеличить последнюю цифру на 1, го имеем число, большее 0,25 (например, 0,3 или 0,251).
Бесконечные десятичные дроби, которые получаются при записи положительного рационального числа, обладают особенностью - они являются периодическими. Это значит, что, начиная с некоторой цифры, они образуются бесконечным повторением одной и той же группы цифр. Например, число  выражается бесконечной десятичной дробью 0,272727... 27..., а число
выражается бесконечной десятичной дробью 0,272727... 27..., а число  бесконечной десятичной дробью 0,1454545...45.... Для краткости первую из дробей пишут в виде 0,(27), а вторую - в виде 0,1(45). В скобки заключают повторяющуюся группу цифр, которую называют периодом этой дроби. Отметим, что вместо 0,(27) можно было написать и 0,2(72), но эта запись более длинная.
бесконечной десятичной дробью 0,1454545...45.... Для краткости первую из дробей пишут в виде 0,(27), а вторую - в виде 0,1(45). В скобки заключают повторяющуюся группу цифр, которую называют периодом этой дроби. Отметим, что вместо 0,(27) можно было написать и 0,2(72), но эта запись более длинная.
Приведенные рассуждения приводят к следующей теореме.
Теорема. Любое положительное рациональное число представимо бесконечной периодической десятичной дробью.
Доказательство. Пусть рациональное число представлено несократимой дробью  . Чтобы преобразовать ее в десятичную, надо выполнить деление натурального числа m на натуральное число n. При этом будут остатки, меньшие n, т.е. числа вида 0, 1, 2,... n - 1. Если хотя бы один из остатков окажется равным нулю, то после деления получится конечная десятичная дробь (или, что то же самое, бесконечная десятичная дробь, заканчивающаяся последовательностью нулей). Если же все остатки отличны от нуля, то деление будет представлять собой бесконечный процесс, но количество различных остатков конечно, и поэтому, начиная с некоторого шага, какой-то остаток повторится, что приведет к повторению цифр в частном.
. Чтобы преобразовать ее в десятичную, надо выполнить деление натурального числа m на натуральное число n. При этом будут остатки, меньшие n, т.е. числа вида 0, 1, 2,... n - 1. Если хотя бы один из остатков окажется равным нулю, то после деления получится конечная десятичная дробь (или, что то же самое, бесконечная десятичная дробь, заканчивающаяся последовательностью нулей). Если же все остатки отличны от нуля, то деление будет представлять собой бесконечный процесс, но количество различных остатков конечно, и поэтому, начиная с некоторого шага, какой-то остаток повторится, что приведет к повторению цифр в частном.
Действительные числа
Одним из источников появления десятичных дробей является деление натуральных чисел, другим - измерение величин. Выясним, например, как могут получиться десятичные дроби мри измерении длины отрезка.
Пусть х- отрезок, длину которого надо измерить, е- единичный отрезок. Длину отрезка х обозначим буквой X, а длину отрезка е - буквой Е. Пусть отрезок х состоит из n отрезков, равных е, и отрезка х1, который короче отрезка е (рис. 3), т.е.

Рис.3
n·Е < X < (n + 1) ·Е. Числа n и n+ 1 есть приближенные значения длины отрезка х при единице длины Е с недостатком и с избытком с точностью до 1.
Чтобы получить ответ с большей точностью, возьмем отрезок е1 - десятую часть отрезка е и будем укладывать его в отрезке х1. При этом возможны два случая.
1) Отрезок е1 уложился в отрезке х1 точно n раз. Тогда длина и отрезка х выражается конечной десятичной дробью:
X =  ·Е=
·Е=  ·Е. Например, X = 3,4·Е.
·Е. Например, X = 3,4·Е.
2) Отрезок х1 оказывается состоящим из n отрезков, равных е1, и отрезка х2, который короче отрезка е1. Тогда  ·Е<Х
·Е<Х  ·Е, где
·Е, где  и
и 
- приближенные значения длины отрезка х с недостатком и с избытком с точностью до 0,1.
Ясно, что во втором случае процесс измерения длины отрезка х можно продолжать, взяв новый единичный отрезок е2 -сотую часть отрезка е.
На практике этот процесс измерения длины отрезка на каком-то этапе закончится. И тогда результатом измерения длины отрезка будет либо натуральное число, либо конечная десятичная дробь. Если же представить этот процесс измерения длины отрезка в идеале (как и делают в математике), то возможны два исхода:
1) На k-том шагу процесс измерения окончится. Тогда длина отрезка х выразится конечной десятичной дробью вида  .
.
2) Описанный процесс измерения длины отрезка х продолжается бесконечно. Тогда отчет о нем можно представить символом  , который называют бесконечной десятичной дробью.
, который называют бесконечной десятичной дробью.
Как убедиться в возможности второго исхода? Для этого достаточно произвести измерение длины такого отрезка, для которого известно, что его длина выражена, например, рациональным числом 5—. Если бы оказалось, что в результате измерения длины такого отрезка получается конечная десятичная дробь, то это означало бы, что число 5  можно представить в виде конечной десятичной дроби, что невозможно: 5
можно представить в виде конечной десятичной дроби, что невозможно: 5  = 5,666....
= 5,666....
Итак, при измерении длин отрезков могут получаться бесконечные десятичные дроби. Но всегда ли эти дроби периодические? Ответ на этот вопрос отрицателен существуют отрезки, длины которых нельзя выразить бесконечной периодической дробью (т.е. положительным рациональным числом) при выбранной единице длины. Это было важнейшим открытием в математике, из которого следовало, что рациональных чисел недостаточно для измерения длин отрезков.
Теорема. Если единицей длины является длина стороны квадрата, то длина диагонали этого квадрата не может быть выражена положительным рациональным числом.
Доказательство. Пусть длина стороны квадрата выражается числом 1. Предположим противное тому, что надо доказать, т.е., что длина диагонали АС квадрата ABCD выражается несократимой дробью  . Тогда по теореме Пифагора, выполнялось бы равенство 12+12=
. Тогда по теореме Пифагора, выполнялось бы равенство 12+12=  . Из него следует, что m2 = 2п2. Значит, m2- четное число, тогда и число m -четно (квадрат нечетного числа не может быть четным). Итак, m = 2р. Заменив в равенстве m2 = 2n2 число m на 2р, получаем, что 4р2 = 2n2, т.е. 2р2 = n2. Отсюда следует, что n2 четно, следовательно, n - четное число. Таким образом, числа m и n чётны, значит, дробь
. Из него следует, что m2 = 2п2. Значит, m2- четное число, тогда и число m -четно (квадрат нечетного числа не может быть четным). Итак, m = 2р. Заменив в равенстве m2 = 2n2 число m на 2р, получаем, что 4р2 = 2n2, т.е. 2р2 = n2. Отсюда следует, что n2 четно, следовательно, n - четное число. Таким образом, числа m и n чётны, значит, дробь  можно сократить на 2, что противоречит предположению о её несократимости. Установленное противоречие доказывает, что если единицей длины является длина стороны квадрата, то длину диагонали этого квадрата нельзя выразить рациональным числом.
можно сократить на 2, что противоречит предположению о её несократимости. Установленное противоречие доказывает, что если единицей длины является длина стороны квадрата, то длину диагонали этого квадрата нельзя выразить рациональным числом.
Из доказанной теоремы следует, что существуют отрезки, длины которых нельзя выразить положительным числом (при выбранной единице длины), или, другими словами, записать в виде бесконечной периодической дроби. И значит, получаемые при измерении длин отрезков бесконечные десятичные дроби могут быть непериодическими.
Считают, что бесконечные непериодические десятичные дроби являются записью новых чисел - положительных иррациональных чисел. Так как часто понятия числа и его записи отождествляют, то говорят, что бесконечные непериодические десятичные дроби - это и есть положительные иррациональные числа.
Мы пришли к понятию положительного иррационального числа через процесс измерения длин отрезков. Но иррациональные числа можно получить и при извлечении корней из некоторых рациональных чисел. Так,  ,
,  ,
, 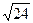 - это иррациональное числа. Иррациональными являются также tg5, sin 31, числа π = 3,14..., е = 2,7828... и другие
- это иррациональное числа. Иррациональными являются также tg5, sin 31, числа π = 3,14..., е = 2,7828... и другие
Множество положительных иррациональных чисел обозначают символом J+.
Объединение двух множеств чисел: положительных рациональных и положительных иррациональных называют множеством положительных действительных чисел и обозначают символом R+. Таким образом, Q+  J+ = R+. При помощи кругов Эйлера эти множества изображены на рисунке 4.
J+ = R+. При помощи кругов Эйлера эти множества изображены на рисунке 4.

Рис.4
Любое положительное действительное число может быть представлено бесконечной десятичной дробью - периодической (если оно является рациональным), либо непериодической (если оно является иррациональным).
Действия над положительными действительными числами сводятся к действиям над положительными рациональными числами.
Сложение и умножение положительных действительных чисел обладает свойствами коммутативности и ассоциативности, а умножения дистрибутивно относительно сложения и вычитания.
С помощью положительных действительных чисел можно выразить результат измерения любой скалярной величины: длины, площади, массы и т.д. Но на практике часто нужно выразить числом не результат измерения величины, а ее изменение. Причем ее изменение может происходить различно - она может увеличиваться, уменьшаться или оставаться неизменной. Поэтому, чтобы выразить изменение величины, кроме положительных действительных чисел нужны иные числа, а для этого необходимо расширить множество R+, присоединив к нему число 0 (нуль) и отрицательные числа.



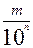 , где m и n- натуральные числа.
, где m и n- натуральные числа. записывают в виде 3,67, а дробь
записывают в виде 3,67, а дробь  в виде 0,007.
в виде 0,007. N. Представим ее числитель в следующем виде:
N. Представим ее числитель в следующем виде:

 представляет дробную часть числа, ее принято записывать без знаменателя в виде
представляет дробную часть числа, ее принято записывать без знаменателя в виде  . Таким образом,
. Таким образом, , т.е. при записи дроби
, т.е. при записи дроби  последние n цифр десятичной записи числа т отделяют запятой. Если числитель содержит менее чем n десятичных знаков, то перед ним пишут столько нулей, чтобы получилась n + 1 цифра, после чего отделяют запятой n знаков, начиная с конца. Например,
последние n цифр десятичной записи числа т отделяют запятой. Если числитель содержит менее чем n десятичных знаков, то перед ним пишут столько нулей, чтобы получилась n + 1 цифра, после чего отделяют запятой n знаков, начиная с конца. Например,  0,0047.
0,0047. приписать справа любое число нулей, то получится десятичная дробь, равная данной.
приписать справа любое число нулей, то получится десятичная дробь, равная данной. +
+  +
+  =6,2526.
=6,2526. . Например, 25%- это дробь
. Например, 25%- это дробь  , или 0,25.
, или 0,25. (m, n
(m, n  нельзя записать в виде десятичной.
нельзя записать в виде десятичной.
 Дробь
Дробь  нельзя представить в виде конечной десятичной дроби. Но, деля 1 на 3, получаем, что 0,3 <
нельзя представить в виде конечной десятичной дроби. Но, деля 1 на 3, получаем, что 0,3 <  выражается бесконечной десятичной дробью 0,272727... 27..., а число
выражается бесконечной десятичной дробью 0,272727... 27..., а число  бесконечной десятичной дробью 0,1454545...45.... Для краткости первую из дробей пишут в виде 0,(27), а вторую - в виде 0,1(45). В скобки заключают повторяющуюся группу цифр, которую называют периодом этой дроби. Отметим, что вместо 0,(27) можно было написать и 0,2(72), но эта запись более длинная.
бесконечной десятичной дробью 0,1454545...45.... Для краткости первую из дробей пишут в виде 0,(27), а вторую - в виде 0,1(45). В скобки заключают повторяющуюся группу цифр, которую называют периодом этой дроби. Отметим, что вместо 0,(27) можно было написать и 0,2(72), но эта запись более длинная.
 ·Е=
·Е=  ·Е. Например, X = 3,4·Е.
·Е. Например, X = 3,4·Е. ·Е, где
·Е, где  и
и  .
. , который называют бесконечной десятичной дробью.
, который называют бесконечной десятичной дробью. можно представить в виде конечной десятичной дроби, что невозможно: 5
можно представить в виде конечной десятичной дроби, что невозможно: 5  . Из него следует, что m2 = 2п2. Значит, m2- четное число, тогда и число m -четно (квадрат нечетного числа не может быть четным). Итак, m = 2р. Заменив в равенстве m2 = 2n2 число m на 2р, получаем, что 4р2 = 2n2, т.е. 2р2 = n2. Отсюда следует, что n2 четно, следовательно, n - четное число. Таким образом, числа m и n чётны, значит, дробь
. Из него следует, что m2 = 2п2. Значит, m2- четное число, тогда и число m -четно (квадрат нечетного числа не может быть четным). Итак, m = 2р. Заменив в равенстве m2 = 2n2 число m на 2р, получаем, что 4р2 = 2n2, т.е. 2р2 = n2. Отсюда следует, что n2 четно, следовательно, n - четное число. Таким образом, числа m и n чётны, значит, дробь  ,
,  ,
, 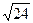 - это иррациональное числа. Иррациональными являются также tg5, sin 31, числа π = 3,14..., е = 2,7828... и другие
- это иррациональное числа. Иррациональными являются также tg5, sin 31, числа π = 3,14..., е = 2,7828... и другие J+ = R+. При помощи кругов Эйлера эти множества изображены на рисунке 4.
J+ = R+. При помощи кругов Эйлера эти множества изображены на рисунке 4.



