6.1. Р е ш е н и е з а д а ч и К о ш и д л я у р а в н е н и й
Рассмотрим задачу наиболее часто встречающую в теории автоматического управления систем – задачу Коши для линейных дифференциальных уравнений.
Пусть задано линейное обыкновенное дифференциальное уравнение с постоянными коэффициентами
x( п ) + a1 x ( п - 1) +... a п x = f(t), (6.1)
где п – порядок уравнения; a 1 , a 2 ,..., a п = const; f (t) – заданная функция.
Требуется найти решение уравнения (6.1), удовлетворяющее начальным условиям, заданным в точке t = t 0:
х (t 0) = x 0, х' (t 0) = х 1 , ..., x (п -1) (t 0) = хп- 1
где x 0, х 1,..., хп- 1 - заданные числа.
Будем предполагать, что искомая функция x (t), все ее рассматриваемые производные, а также функция f (t) являются оригиналами.
При решении поставленной задачи операционным методом различают д в а с л у ч а я н а ч а л ь н ы х у с л о в и й: начальные условия заданы в т о ч к е t 0 = 0 и в т о ч к е t 0 ≠ 0.
П е р в ы й с л у ч а й: начальные условия заданы в т о ч к е t 0 = 0, т.е.:
х (0) = x 0, х' (0) = х1 ,..., x (п- 1) (0) = хп- 1 (6.2)
При т а к и х начальных условиях, обозначив x (t) ≓ Х (p) и f (t) ≓ F (p), с р а з у применим к обеим частям уравнения (6.1) преобразование Лапласа, используя при этом теорему о дифференцировании оригинала (3.4):
х′ (t) ≓ р Х(p) - х (0),
х′′(t) ≓ р2 Х (p) - р х (0) - х' (0)и так далее…
и свойство линейности изображения. В результате получим вместо дифференциального уравнения (6.1) с начальными условиями (6.2) операторное уравнение или уравнение в изображениях:
(рп + a1 p п - 1 +... + ап) X(p) - Rn- 1 (p) = F(р), (6.3)
где Rn - 1 (p) - многочлен от р степени n – 1, коэффициенты которого зависят от начальных данных x 0, х1 ,..., хп- 1 и который тождественно равен н у л ю, если х (0) = х' (0) =...= x (п -1) (0) = 0.
Полученное алгебраическое уравнение (6.3) всегда можно представить в виде:
Qn (p) X(p) - Rn- 1 (p) = F(р). (6.4)
Многочлен от р степени n Qn (p)= рп + a 1 p п- 1 +... + ап называется характеристическим многочленом данного уравнения.
Разрешая уравнение (6.4) относительно X (p), находим операторное решение дифференциального уравнения (6.1):
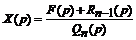 . (6.5)
. (6.5)
Оригинал x (t), для которого функция (6.5) является изображением, и будет искомым решением задачи Коши.
В т о р о й с л у ч а й: начальные условия заданы в т о ч к е t 0 ≠ 0.
В этом случае перед применением операционного метода
н е о б х о д и м о п р е о б р а з о в а т ь у с л о в и е поставленной задачи: сделать линейную замену независимой переменной t = τ + t 0 , чтобызадача Коши при t = t 0 ≠ 0 свелась к задаче с начальными условиями в точке τ = 0 (к случаю 1)
Например (см. также пример 6.4), рассмотрим для простоты дифференциальное уравнение второго порядка
x ′′ + a 1 x ′ + a 2 x = f (t). (6.6)
Пусть требуется найти его решение, удовлетворяющее начальным условиям:
х (t 0) = x 0и х' (t 0 ) = х 1,где t 0 ≠ 0
Положим t = τ + t 0и сделаемв уравнении(6.6) замену:
х (t) = х (t 0 + τ) = х (τ), f (t) = f (τ + t 0) = f (τ),
х ′ (t) = х ′ (τ + t 0) = х ′ (τ), х ′′ (t) = х ′′ (τ + t 0) = х ′′ (τ).
Получим задачу Коши для уравнения
x ′′ + a 1 x ′ + a 2 x = f (τ)
с начальными условиями, заданными в точке τ = 0:
х (0) = x 0 и х' (0) = х 1 (задача свелась к случаю 1).
Операционный метод интегрирования линейных дифференциальных уравнений перед классическими методами имеет
п р е и м у щ е с т в а:
1) сразу получается решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, минуя получение общего интеграла этого уравнения. Если требуется, то можно найти общий интеграл дифференциального уравнения операционным методом (см. пример 6. 5);
2) метод применим, если правая часть рассматриваемого дифференциального уравнения является р а з р ы в н о й функцией, которую в классическом анализе обычно записывают с помощью нескольких различных аналитических выражений (см. пример 6.6).
Пример. 6.1. Решить задачу Коши
x ′′ + x = 2 cos t; х (0) = 0, х' (0) = - 1.
Решение. Пусть x (t) ≓ Х (p). Применим к обеим частям заданного уравнения преобразование Лапласа. Учитывая, что
х′′(t) ≓ р 2 Х (p) - р х (0) - х' (0) = р 2 Х (p)+ 1 и cos t ≓  , получим операторное уравнение:
, получим операторное уравнение:
р 2 Х (p) + 1 + Х (p) = 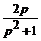 , т.е. (р2 + 1) Х (p) =
, т.е. (р2 + 1) Х (p) =  .
.
Найдем операторное решение дифференциального уравнения:
Х (p) = 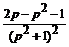 . Полученную дробь Х (p) разобьем на сумму простейших: Х (p) =
. Полученную дробь Х (p) разобьем на сумму простейших: Х (p) =  .
.
Восстановим оригинал для Х (p). Для этого, например, воспользуемся таблицей изображений функций (см. главу 2):
 ≒ t sin t;
≒ t sin t; 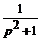 ≒ sin t.
≒ sin t.
Итак, искомое решение x (t) = t sin t - sin t = (t – 1) sin t.
Пример. 6.2. Найти решение уравнения x ′′′ (t) + 4 x ′ (t) = 1, удовлетворяющее условиям
х (0) = х' (0) = х'′ (0) = 0.
Решение. Пусть x (t) ≓ Х (p). Операторное уравнение при нулевых начальных условий имеет вид: р 3 Х (p) + 4 рХ (p) =  .
.
Отсюда Х (p) = 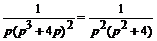 . Так как
. Так как
 =
=  , то,
, то,
выполнив обращение, найдем искомое решение x (t) =  .
.
Пример. 6.3. Найти решение уравнения x ′′ + x ′ - 2 х = е t, удовлетворяющее условиям: х (0) = -1, х' (0) = 0.
Решение. Пусть x (t) ≓ Х (p). Переходим к уравнению в изображениях р 2 Х (p) + р +рХ (p) + 1 – 2 Х (p) =  . Отсюда
. Отсюда
Х (p) = 
 .
.
Представим изображение Х (p) в виде суммы простейших:
Х (p) = 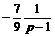 +
+  .
.
Переходя от изображений к оригиналам, получим искомое решение: x (t) = 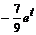 +
+ 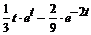 .
.
Пример. 6.4. Найти решение уравнения x ′′ (t) + x ′ (t) = t,
удовлетворяющее начальным условиям: х (1) = 1, х ′ (1) = 0.
Решение. Положим t = τ + 1 и х (t) = х (τ + 1) = х (τ).
х ′ (t) = х ′ (τ + 1) = х ′ (τ),, х ′′ (t) = х ′′ (τ + 1) = х ′′ (τ).



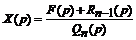 . (6.5)
. (6.5) , получим операторное уравнение:
, получим операторное уравнение: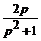 , т.е. (р2 + 1) Х (p) =
, т.е. (р2 + 1) Х (p) =  .
.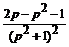 . Полученную дробь Х (p) разобьем на сумму простейших: Х (p) =
. Полученную дробь Х (p) разобьем на сумму простейших: Х (p) =  .
. ≒ t sin t;
≒ t sin t; 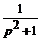 ≒ sin t.
≒ sin t. .
.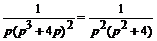 . Так как
. Так как  =
=  , то,
, то,  .
. . Отсюда
. Отсюда
 .
.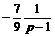 +
+  .
.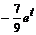 +
+ 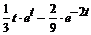 .
.

