Операционное исчисление
Электронный конспект лекций
Осипова В.А.
Максимова Н.М.
Красноярск 2004
ПРИМЕНЕНИЕ ТЕОРЕМЫ ЗАПАЗДЫВАНИЯ
ДЛЯ НАХОЖДЕНИЯ ИЗОБРАЖЕНИЙ РАЗРЫВНЫХ ФУНКЦИЙ (ИМПУЛЬСОВ).
Пустьзадана некоторая функция φ(t), график которой представлен на рис. 4.1. При умножении этой функции φ(t) на функцию Хевисайдаполучается функция-оригинал:
 (4.1)
(4.1)
т.е. в результате умножения произошло обнуление значений заданной функции φ (t) при t < 0 (рис.4.2).

| 
|
| Рис. 4.1.
| Рис.4.2.
|
Рассмотрим теперь функцию - оригинал f (t), график которой представлен на рис. 4.3. Тогда функция
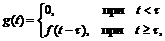 (4.2)
(4.2)
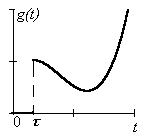
где τ – положительное число, имеет график (рис.4.4), который получается из графика f (t) сдвигом последнего на величину τ вдоль оси t. Таким образом, если функция f (t) определяет течение во времени некоторого процесса, то функция g (t) определяет тот же процесс, но начавшийся с опозданием τ. 

| 
|
| Рис. 4.3.
| Рис.4.4.
|
С помощью единичной функции Хевисайда запаздывающую на τ функцию g (t) (4.2) можно записать в виде:
g (t) = h (t - τ) ·f (t – τ), (4.3)
так как h (t - τ) = 0 при t < τ (в этом случае аргумент отрицателен) и 1 при t ≥ τ.
При нахождении изображения оригинала в случае, когда его аргумент запаздывает, используется т е о р е м а з а п а з д ы в а н и я: если f (t) ←÷ F (p), то запаздывание аргумента оригинала на τ > 0 приводит к умножению изображения оригинала без запаздывания на
е - рτ, т. е.
h (t - τ) f (t – τ) ≓ е - рτ F (p). (4.4)
Пример 4.1. Найти изображение оригинала f (t)= е t - 2 h (t - 2 ).
Решение. Здесь f (t) есть функция е t, но включаемая с «запаздыванием» τ = 2. Так как е t ≓  , то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓
, то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓  .
.
З а м е ч а н и е. Если в записи f (t) опустить множитель h (t - 2 ), то получится функция е t – 2, которая означает оригинал е t - 2 h (t) без запаздывания смотри формулу (4.1)). Изображением этого оригинала будет:
е t - 2 h (t) = е – 2· е t h (t) ≓ 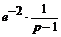 .
.
Таким образом, н е д о п у с т и м о опускать множители вида h (t - τ) в записи функций (см. также пример 3.5).

| 
|
| Рис. 4.5.
| Рис.4.6.
|
Пример 4.2. Найти изображение функций f 1 (t) и f 2 (t), представленных соответственно на рис. 4.5 и 4.6.
Решение. Первая функция f 1 (t) есть импульс величины 4, «включаемый» в момент t = 0 и «погашаемый» в момент τ = 2; следовательно, согласно (4.3) запишем: f 1 (t)= 4· h (t) - 4· h (t - 2).
Аналитическое выражение функции f 2 (t) найдем, рассуждая следующим образом: в момент t = 0 появился импульс величины 2 - запишем: f 2 (t) = 2· h(t).
Затем в момент τ = 1 импульс увеличился на 2:
f 2 (t) = 2· h(t) + 2· h (t - 1 ).
Получившийся импульс в момент τ = 2 уменьшился на 3:
f 2 (t) = 2 · h(t) + 2· h (t - 1 ) - 3· h (t - 2).
Далее в момент τ = 3 исследуемый импульс, уменьшившись на 1, стал равным 0 (исчез); т.е. окончательное выражение для f 2 (t) запишется в виде:
f 2 (t) = 2 · h(t) + 2· h (t - 1) - 3· h (t - 2 ) -1· h (t - 3).
Применяя теорему запаздывания(4.4), находим:
f 1 (t) ≓  -
-  =
=  .
.
f 2 (t) ≓ 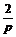 +
+  -
-  -
-  .
.
З а м е ч а н и е. В рассматриваемом примере импульс имел
п р я м о у г о л ь н у ю форму, поэтому удобно было в момент изменения его формы сразу «гасить» или «увеличивать» его на наблюдаемую величину. В случае импульса более сложной формы при нахождении его аналитического описания удобнее в момент изменения формы «гасить» его до нуля и сразу «включать» импульс требуемой формы (см. примеры 4.3 и 4.4).
Пример 4.3. Построить график функции
f (t)= (t 2 - 6 t + 11)· h (t – 2) и найти ее изображение.
Решение. Функция f (t) описывает некоторый процесс φ(t), «включаемый» с запаздыванием τ = 2. Для того, чтобы решить, какой это процесс, нужно представить заданную функцию в форме:
f (t) = φ (t - 2) 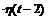 .
.
Сделаем это:
f (t)= (t 2 - 6 t + 11)· h (t – 2) =[(t – 2)2 + 4 t – 4 - 6 t + 11]· h (t – 2) =
=[(t – 2)2 – 2 t + 7)]· h (t – 2) = [(t – 2)2 – 2(t - 2)+ 3)]· h (t – 2).
Отсюда следует, что f (t) есть процесс φ(t) = t 2 – 2 t + 3, «включаемый» с запаздыванием τ = 2. На рис.4.7 представлены графики функций f (t) и φ(t). Так как
φ(t) = t 2 – 2 t + 3 ≓  -
-  +
+  ,
,
то применяя теорему запаздывания, находим:
f(t) = φ (t - 2 ) 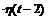 ≓ (
≓ ( -
-  +
+  )
) 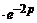 .
.

| 
|
| Рис. 4.7.
| Рис.4.8.
|
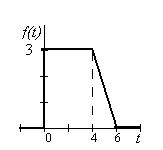
Пример 4.4. Найти изображение функций f (t), представленной на рис. 4.8.
Решение. Запишем заданную функцию в аналитическом виде:
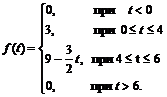
С помощью единичной функции Хевисайда запишем f (t) одним аналитическим выражением:
В момент t = 0 «включается» функция, равная 3, следовательно, f (t) = 3 · h (t).
В момент τ = 4 функция, равная 3, «гасится» и «включается» функция  : f (t) = 3 · h (t) - 3 · h (t - 4) +
: f (t) = 3 · h (t) - 3 · h (t - 4) +  .
.
В момент τ = 6 функция  «гасится» (сигнал исчез), следовательно, искомое выражение функции имеет вид:
«гасится» (сигнал исчез), следовательно, искомое выражение функции имеет вид:
f(t) = 3 · h (t) - 3 · h (t - 4) +  -
- 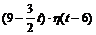
или f(t) = 3 · h (t) +  -
- 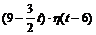 .
.
Чтобы найти изображение этой функции, нужно представить ее в следующей форме (см. также пример 4.3):
f (t) = 3 · h (t) + φ 1(t - 4) 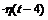 - φ2(t - 6 )
- φ2(t - 6 )  .
.
Выполним следующие преобразования:
f (t) = 3 · h (t) + [ 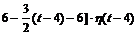 -
-  =
=
= 3 · h (t) 
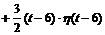 .
.
Так как
φ1(t)= 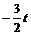 ≓
≓ 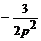 и φ 2(t - 6) =
и φ 2(t - 6) =  ←÷
←÷ 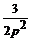 ,
,
то, применяя теорему запаздывания (4.4), находим:
f (t) ≓ 
 +
+  .
.
Пример 4.5. Найти оригинал по его изображению:
а) F (p)= 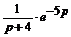 ; б) F (p)=
; б) F (p)=  .
.
Решение. а) учитывая, что  ≒
≒  , по теореме запаздывания (4.4) находим:
, по теореме запаздывания (4.4) находим: 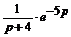 ≒
≒ 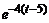
 .
.
б) так как  ≒
≒ 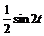 , применим (4.4) и получим:
, применим (4.4) и получим:
 ≒
≒ 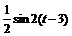
 .
.
ВОССТАНОВЛЕНИЕ ОРИГИНАЛА
ПО ИЗОБРАЖЕНИЮ
В операционном исчислении обратная задача - определение оригинала f (t) по известному изображению F (p), является одной из главных.
Важным частным случаем изображений являются изображения F (p) в виде правильных (m < n) и неправильных (если m ≥ n) рациональных дробей:
 , (5.1)
, (5.1)
где Qm (p) и Rn (p) - многочлены от р степени m и n соответственно.
Неправильность дроби указывает, что оригинал будет содержать дельта функцию Дирака δ(t) или ее производные.
Во многих случаях заданное изображение можно преобразовать к такому виду, когда оригинал легко восстанавливается непосредственно с помощью свойств преобразования Лапласа и таблицы изображений. Иногда задачу удается решить с помощью теоремы об изображении свертки.
Изображения F (p) в виде неправильной рациональной дроби, удобно п р е д в а р и т е л ь н о п р е о б р а з о в а т ь: выделить в этой дроби, разделив числитель на знаменатель (по правилу деления многочленов «уголком»), целую часть – многочлен Mm - n (p) степени
m - n, и некоторую правильную дробь 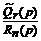 :
:

где Q ̃ r (p) - многочлен степени r, причем r < n.
П р и о б р а щ е н и и изображения в виде многочлена используетсясвойство линейности изображения и соответствие:
р к ÷→ δ (к)(t) (к = 0,1,...)
П р и о б р а щ е н и и изображения в виде правильной рациональной дроби 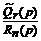 широко используется следующий прием: разлагают эту дробь в сумму простейших дробей методом неопределенных коэффициентов и находят оригиналы для каждой.
широко используется следующий прием: разлагают эту дробь в сумму простейших дробей методом неопределенных коэффициентов и находят оригиналы для каждой.
Пример 5.1. Найти оригинал f (t), если  .
.
Решение. П е р в ы й с п о с о б. Выделяя полный квадрат в знаменателе и далее, используя табличное изображение (10), получим:
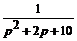 =
= 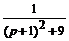 =
=  ≒
≒ 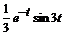 .
.
В т о р о й с п о с о б. Раскладывая дробь в сумму простейших, используя изображение для е at, получим
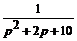 =
=  -
- 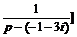 ≒
≒
≒  =
= 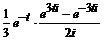 =
= 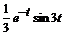 .
.
Пример 5.2. Найти оригинал f (t), если  .
.
Решение. П е р в ы й с п о с о б. Используем теорему Бореля об изображении свертки, получим
 =
= 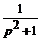 ·
· 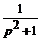 ≒
≒  *
*  =
=  =
=
= 
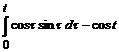
 =
= 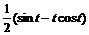 .
.
В т о р о й с п о с о б. Раскладывая дробь в сумму простейших, используя изображение для е at, получим
 =
= 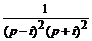 =
= 
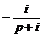 +
+ 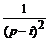 +
+  ÷→
÷→
≒ 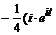
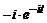 +
+  +
+ 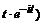 =
= 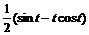 .
.
Пример 5.3. Найти оригинал f (t), если 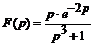 .
.
Решение. Найдем сначала оригинал для дроби 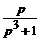 , разложив ее в сумму простейших:
, разложив ее в сумму простейших:
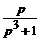 =
= 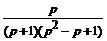 =
=  +
+ 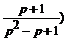 =
=
= 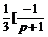 +
+  =
= 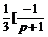 +
+  +
+ 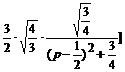
≒ 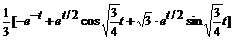 .
.
Учтем теперь сомножитель е –2 р : применив теорему запаздывания, найдем
 ≒
≒  .
.
Положим
y (t) = x (t) - x 0 - х 1 t. (7.5)
Тогда y′ (t) = x′ (t) - х 1, y′′ (t) = x′′ (t),
Операционное исчисление
Электронный конспект лекций
Осипова В.А.
Максимова Н.М.
Красноярск 2004
ФУНКЦИЯ ЛАПЛАСА. ОПРЕДЕЛЕНИЕ И СВОЙСТВА
Оригиналом или начальной функцией называется любая функция f (t), удовлетворяющая условиям:
1) f (t) = 0 при t < 0, причем принимается, что f (0)= f (+0);
2) | f (t) | возрастает при t ® + ¥ не быстрее показательной функции, т. е. существуют такие постоянные s и М, что
| f(t) | < Mest при t > 0 (1.1)
3)на любом конечном отрезке [0,T] положительной полуоси Ot функция f (t) удовлетворяет у с л о в и я м Д и р и х л е, т.е.:а) ограничена; б) либо непрерывна, либо имеет лишь конечное число точек разрыва 1 –ого рода; в) имеет конечное число экстремумов.
Величина s 0 = inf s называется показателем роста функции f (t). Для любой ограниченной функции, являющейся оригиналом, можно принять s 0 = 0.
Простейшими оригиналами, например, являются:
а) тригонометрический синус и косинус
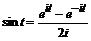 и
и  ; (1.2)
; (1.2)
б) г и п е р б о л и ч е с к и й синус и косинус
 и
и  ; (1.3)
; (1.3)
в) единичная функция Х е в и с а й д а - h (t), (обозначается также как s 0 (t) или 1 (t))
 (1.4)
(1.4)
При умножении любой функции j (t) на функцию Хевисайдаполучается функция:
 (1.5)
(1.5)
З а м е ч а н и е. В практике операционного исчисления приходится сталкиваться с так называемыми обобщенными функциями. Одним из представителей которых является функция Д и р а к а δ (t), которая определяется так:
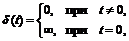 ;
;  (1.6)
(1.6)
где 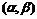 - любой интервал, содержащий точку t = 0, а f (t) – функция, непрерывная в точке t = 0.
- любой интервал, содержащий точку t = 0, а f (t) – функция, непрерывная в точке t = 0.
Аналогично определяется функция δ (t - t), сосредоточенная в точке t = t.
В теории обобщенных функций δ (t) рассматривается как производная единичной функции Хевисайда
h ′ (t) = δ (t). (1.7)
Преобразованием Лапласа от функции f (t), или лапласовым изображением функции f (t), или L -изображением f (t) называется функция F (p) комплексного переменного p = s + i s, определяемого равенством
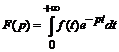 (1.8)
(1.8)
Если f (t) - оригинал, то стоящий в правой части равенства (1.8) интеграл Лапласа сходится абсолютно и равномерно в полуплоскости
Re p ³ s > s 0; при этом функция F(р) является аналитической.
С о о т в е т с т в и е между оригиналом f (t) и его изображением F (р) символически записывается в виде:
F (p) ÷→ f (t), или f (t) ←÷ F (p), или F (p) = L { f (t)},
а также F (p) ≒ f (t), или f (t) ≓ F (p).
Если оригинал обозначен другой буквой, то, как правило, для обозначения его изображения вводится соответствующая прописная буква. Например:
φ(t) ≓ Φ(p); X (p) ÷→ x (t); Y (p) = L { y (t) }.
Операция перехода от оригинала f (t) к изображению F (p) называется преобразованием Лапласа.
C в о й с т в а п р е о б р а з о в а н и я Л а п л а с а
Т е о р е м а е д и н с т в е н н о с т и. Преобразование Лапласа (1.6) единственно в том смысле, что две функции f 1 (t) и f 2 (t), имеющее одно и тоже изображение F (p), совпадают во всех точках
н е п р е р ы в н о с т и для всех t ³ 0.
Уславливаются за значение оригинала f (t) во всякой его точке разрыва 1 –ого рода t 0 принимать полусумму его предельных значений слева и справа от этой точки:
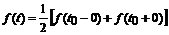 .
.
При соблюдении этого условия соответствие между оригиналами и изображениями в з а и м н о о д н о з н а ч н о (т.е. всякому оригиналу соответствует единственное изображение и обратно).
С в о й с т в о л и н е й н о с т и. Если L { f (t)}= F (p) и
L { φ (t)}= Φ(p), то тогда для любых постоянных α и β
L { α f (t)+ β φ(t) } = α F (p)+ β Φ (p).
(Свойство линейности остается справедливым для любого конечного числа слагаемых).
Пример.1.1. Показать, что функция  являетсяоригиналом.
являетсяоригиналом.
Решение. Чтобы доказать, что заданная функция f (t) является оригиналом необходимо (в соответствии с определением) проверить выполнение трех условий.
Условие 1 выполнено в силу задания функции.
Так как  , то в качестве М в условии 2 можно взять любое число ³ 1, s 0 = 3.
, то в качестве М в условии 2 можно взять любое число ³ 1, s 0 = 3.
Функция f (t) удовлетворяет условиям Дирихле: на любом конечном отрезке она ограничена, непрерывна, имеет конечное число экстремумов - условие 3 также выполнено.
Пример.1.2. Проверить, являются ли функции 

 оригиналами.
оригиналами.
Решение. Функция f 1 (t) является оригиналом, т. к. условия 1-3 выполнены: М = 4, s 0 = 5; функция f 2 (t) не является оригиналом, так как в точке t = 5 имеет разрыв второго рода (не выполняется условие Дирихле; f 3 (t) не является оригиналом, так растет быстрее показательной функции (не выполняется условие 2, поскольку  > Mest для любых М и s при t > 0).
> Mest для любых М и s при t > 0).
Пример.1.3. Пользуясь определением, найти изображение функции Хевисайда (1.4).
Решение. Так как функция Хевисайда является оригиналом с показателем роста s 0 = 0, то по формуле (1.8)
L { h (t) }= 
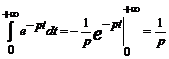 при Re p > 0.
при Re p > 0.
2. ОСНОВНЫЕ ОРИГИНАЛЫ И ИХ ИЗОБРАЖЕНИЯ
Если функция f (t) удовлетворяет условиям 2 и 3, накладываемых на оригинал, но не удовлетворяет условию 1 (f (t) = 0 при t < 0), то функция h (t) × f (t), «погашенная» при t < 0, уже будет оригиналом. В дальнейшем будем считать, что рассматриваемые нами функции снабжены множителем h (t), хотя сам этот множитель в написании часто будем опускать. Так, например, мы можем написать tn, sin ωt, eat и т. д., подразумевая при этом соответственно h (t) × tn, h (t) × sin ωt, h (t) × eat и т. д.
Т а б л и ц а и з о б р а ж е н и й о с н о в н ы х
ф у н к ц и й.
|
№
|
Оригинал h (t) × f (t).
|
Изображение F (p).
|
| 1.
|
Функция Хевисайда
h (t)
| 
|
|
2.
|
tn
(n - натуральное число)
| 
|
|
3.
|
t а
(Re а > -1)
| 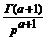
|
|
4.
|
eat
| 
|
|
5.
|
tn eat
| 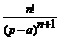
|
|
6.
|
sin ωt
(ω> 0)
| 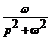
|
|
7.
|
cos ωt
| 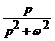
|
|
8.
|
sh ωt
(ω> 0)
| 
|
|
7.
|
ch ωt
| 
|
|
10.
|
eat sin ωt
(ω> 0)
| 
|
|
11.
|
eat cos ωt
| 
|
|
12.
|
eat sh ωt
(ω> 0)
| 
|
|
13.
|
eat ch ωt
| 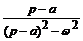
|
|
14.
|
t sin ωt
(ω> 0)
| 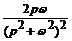
|
|
15.
|
t cos ωt
| 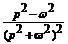
|
|
16.
|
t sh ωt
(ω> 0)
| 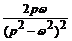
|
|
17.
|
t ch ωt
| 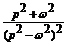
|
|
18.
|
t eat sin ωt
(ω> 0)
| 
|
|
19.
|
t eat cos ωt
| 
|
| 20.
|
h (t - τ)
| 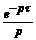
|
| 21
|

|
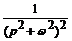
|
| 22.
|

|

|
| 23.
|
Функция Дирака (импульсная функция)
δ (t)
|
1
|
| 24.
|
δ(п) (t)
(п = 1,2,3,….)
|
p n
|
| 25.
|
δ (t - τ)
|

|
З а м е ч а н и е. При определении оригиналов с помощью таблицы полезно помнить следующие формулы:
cosα ∙ cosβ =  [ cos (α – β) + cos (α + β) ]. (2.1)
[ cos (α – β) + cos (α + β) ]. (2.1)
sinα ∙ cosβ =  [ sin (α + β) + sin (α - β) ]. (2.2)
[ sin (α + β) + sin (α - β) ]. (2.2)
sinα ∙ sinβ =  [ cos (α – β) - cos (α + β) ]. (2.3)
[ cos (α – β) - cos (α + β) ]. (2.3)
cos 2 α =  [1 + cos 2 α ], sin 2 α =
[1 + cos 2 α ], sin 2 α =  [1 - cos 2 α ]. (2.4)
[1 - cos 2 α ]. (2.4)
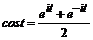 ,
, 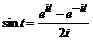 . (2.5)
. (2.5)
Пример 2.1. Пользуясь таблицей изображений функций и свойством линейности, найти изображение функции
f (t)= 3 e - 2 t + 4 sin 5 t - ch( 5 t) et.
Решение. Применив последовательно формулы (4),(6) и (13), получим:  .
.
Пример 2.2. Найти изображение функции f (t)= sh 3 t · sin 4 t.
Решение. Преобразуем заданную функцию, используя определение гиперболического синуса (1.2):
f (t)=  [ e 3 t sin 4 t - e - 3 t sin 4 t ].
[ e 3 t sin 4 t - e - 3 t sin 4 t ].
Применим теперь дважды формулу (10), получим:
 .
.
Пример 2.3. Найти изображение функции
f (t)= e - 4 t sin 3 t · cos 2 t.
Решение. Преобразуем заданную функцию f (t) с помощью формулы (2.2):
f (t)= e - 4 t ·  [ sin ( 3+2 )t + sin ( 3-2 )t ] =
[ sin ( 3+2 )t + sin ( 3-2 )t ] =  e - 4 t [ sin 5 t + sin t ].
e - 4 t [ sin 5 t + sin t ].
Для получения изображения f (t) применим формулу (10):
 .
.
Пример 2.4. Найти изображение функции f (t)= sin 2 4 t.
Решение. С помощью формулы (2.4) запишем f (t) в виде:
f (t)=  [1 – cos 8 t ]. Далее используем формулы(1) и (7):
[1 – cos 8 t ]. Далее используем формулы(1) и (7): 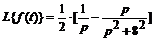 .
.
Пример 2.5. Найти изображение функции f (t)= со s 3 t.
Решение. Воспользуемся формулой (2.5):
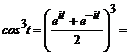
 =
=
=  +
+  =
= 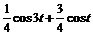 .
.
Применив формулу (7), получим:  .
.
Пример 2.6. Найти изображение функции f (t)= а t.
Решение. Так как а = е ln a, то f (t)= e t ln a. Применив формулу (4), получим: 
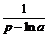 .
.
3. ОСНОВНЫЕ ТЕОРЕМЫ ОПЕРАЦИОННОГО
ИСЧИСЛЕНИЯ
Если L - изображением оригинала f (t) с показателем роста s 0 является функция F (p), т.е. f (t) ≓ F (p), то справедливы следующие теоремы.
1.Теорема подобия. Для любой постоянной α >0
 ≓
≓  , Re p > α s 0. (3.1)
, Re p > α s 0. (3.1)
2. Теорема смещения. Умножению оригинала на eαt,
α? R, соответствует смещение аргумента изображения на α, т.е.
eαtf(t) ≓ F (p - α), R е (p - α) > s0. (3.2)
3. Теорема запаздывания. Запаздыванию оригинала
на τ соответствует умножение изображения на е- рτ , т. е.
h (t - τ) f (t – τ) ≓ е- рτ F (p), Re р > s 0 (3.3)
4. Дифференцирование оригинала. Если функции
f (t), f ´(t),..., f (п) (t) являются оригиналами , то
f ´ (t) ≓ р F (p) - f (0),
f ´´(t) ≓ р2 F (p) - р f (0) - f ´ (0),
.............................
f ( n ) (t) ≓ рп F (p) – рп-1 f (0) – рп-2 f ´ (0) - ... - f ( n -1) (0), (3.4)
где под f (к) (0) (к = 1,2,..., п – 1) понимается  .
.
В частности, при нулевых начальных условиях, т.е. при
f (0) = f ´(0) = ... = f (п-1) (0) = 0 формулы (3.4) упрощается:
f ´ (t) ≓ р F (p),
f ´´(t) ≓ р2 F (p),
.....................
f ( n ) (t) ≓ рп F (p). (3.5)
5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т.е.
 ≓
≓ 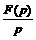 , Re р > s 0 (3.6)
, Re р > s 0 (3.6)
6.Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (- t) оригинала:
F ´ (p) ≒ - tf (t),
F ´´ (p) ≒ t 2 f (t),
....................
F (п) (p) ≒ (- t) n f (t); (3.7)
т.е. умножение оригинала на множитель t соответствует умножение изображения на (- 1) и дифференцирование его по аргументу р:
t n f (t) ≓ (- 1) n F (п) (p), п = 1, 2,... (3.8)
7. Интегрирование изображения. Если  является оригиналом, то
является оригиналом, то
 ≓
≓ 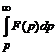 (3.9)
(3.9)
8. Теорема Бореля об изображении свертки (теорема умножения). Если f (t) ≓ F (p) и φ(t) ≓ Φ(p), то произведение двух изображений F (p) и Φ(p) также является изображением, причем
F (p)Φ(p) ≒  . (3.10)
. (3.10)
Интеграл в правой части формул (3.10) называется сверткой (складкой)функций f (t) и φ(t) и обозначается символом f (t)* φ(t). Операция получения свертки называется свертыванием двух функций.
Свертка – операция коммутативная:
f (t)* φ(t) = φ(t) * f (t),
поэтомупроизведение F (p)Φ(p) можно записать в виде:
F (p)Φ(p) ≒  . (3.11)
. (3.11)
Операция свертки может быть применена и к большему числу функций: f (t) = f 1 (t)* f 2 (t)*... * fn (t), причем порядок свертывания роли не играет.
9. Интеграл Дюамеля. Если f (t) ≓ F (p) и φ(t) ≓ Φ(p), то
р F (p)Φ(p) ≒ f (t) φ(0) +  (3.12)
(3.12)
В силу равноправности функций f (t) и φ(t) формулу (3.12) можно переписать так:
р F (p)Φ(p) ≒ f (0) φ(t) + 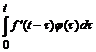 (3.13)
(3.13)
10. Изображение периодических оригиналов. Если f (t) – периодический оригинал с периодом Т, т.е. f (t + Т) = f (t) для всех t > 0, то его изображение F (p) определяется формулой:

 (3.14)
(3.14)
Пример 3.1. Найти изображения функции f (t) = t 2 cos 2 t.
Решение. Найдем изображение заданной функции двумя способами.
П е р в ы й с п о с о б. Согласно формуле (2.5) 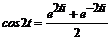 . Подставим его значение в заданную функцию, получим:
. Подставим его значение в заданную функцию, получим:  . Применив формулу (5) таблицы изображений функций, получим:
. Применив формулу (5) таблицы изображений функций, получим:
L { f (t) }=  = =
= = 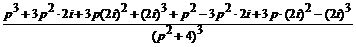 =
=

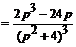 .
.
В т о р о й с п о с о б. Обозначим через f 1 (t) = t × cos 2 t. Найдем по таблице:
L { f 1 (t) }= F (p) =  . По теореме дифференцирования изображения (3.7): t × f 1 (t) ≓ - F ¢ (p), т. е.
. По теореме дифференцирования изображения (3.7): t × f 1 (t) ≓ - F ¢ (p), т. е.
L { t × f 1(t) } = L { t2 cos 2 t } = 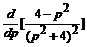 =
=
=  =
=  .
.
Пример 3.2. Найти изображение функции f (t) = t е - t sh t.
Решение. Найдем изображение заданной функции двумя способами.
П е р в ы й с п о с о б. Подставим в заданную функцию значение sh t (1.3), получим:  . Применив формулы (4-5) таблицы изображений функций, получим:
. Применив формулы (4-5) таблицы изображений функций, получим:
L { f (t) }=  ..
..
В т о р о й с п о с о б. О



 (4.1)
(4.1)

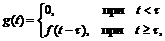 (4.2)
(4.2)


 , то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓
, то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓  .
.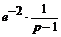 .
.

 -
-  =
=  .
.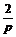 +
+  -
-  -
-  .
.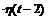 .
.  -
-  +
+  ,
, 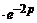 .
.

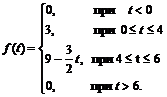
 : f (t) = 3 · h (t) - 3 · h (t - 4) +
: f (t) = 3 · h (t) - 3 · h (t - 4) +  .
.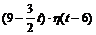
 -
- 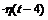 - φ2(t - 6 )
- φ2(t - 6 )  .
.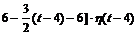 -
-  =
=
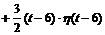 .
.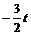 ≓
≓ 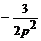 и φ 2(t - 6) =
и φ 2(t - 6) =  ←÷
←÷ 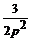 ,
, +
+  .
.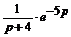 ; б) F (p)=
; б) F (p)=  .
.  ≒
≒  , по теореме запаздывания (4.4) находим:
, по теореме запаздывания (4.4) находим: 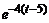
 .
. ≒
≒ 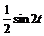 , применим (4.4) и получим:
, применим (4.4) и получим: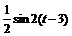
 .
. , (5.1)
, (5.1)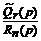 :
:
 .
.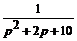 =
= 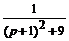 =
=  ≒
≒ 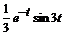 .
. -
- 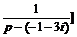 ≒
≒ =
= 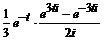 =
=  .
. =
= 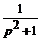 ·
·  *
*  =
=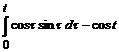
 =
= 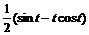 .
.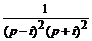 =
= 
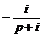 +
+ 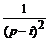 +
+  ÷→
÷→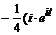
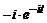 +
+  +
+ 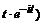 =
= 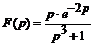 .
.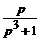 , разложив ее в сумму простейших:
, разложив ее в сумму простейших: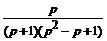 =
=  +
+ 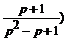 =
=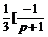 +
+  =
=  +
+ 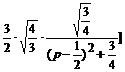
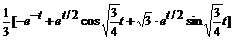 .
. ≒
≒  .
.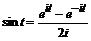 и
и  ; (1.2)
; (1.2)  и
и  ; (1.3)
; (1.3) (1.4)
(1.4)  (1.5)
(1.5)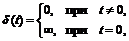 ;
;  (1.6)
(1.6)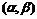 - любой интервал, содержащий точку t = 0, а f (t) – функция, непрерывная в точке t = 0.
- любой интервал, содержащий точку t = 0, а f (t) – функция, непрерывная в точке t = 0.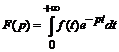 (1.8)
(1.8)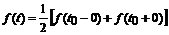 .
. являетсяоригиналом.
являетсяоригиналом.  , то в качестве М в условии 2 можно взять любое число ³ 1, s 0 = 3.
, то в качестве М в условии 2 можно взять любое число ³ 1, s 0 = 3.

 оригиналами.
оригиналами.  > Mest для любых М и s при t > 0).
> Mest для любых М и s при t > 0).
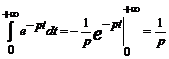 при Re p > 0.
при Re p > 0.

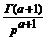

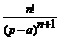
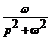
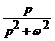





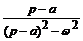
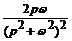
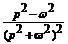
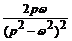
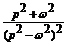


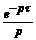

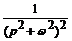



 [ cos (α – β) + cos (α + β) ]. (2.1)
[ cos (α – β) + cos (α + β) ]. (2.1)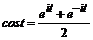 ,
, 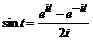 . (2.5)
. (2.5) .
. .
. .
.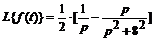 .
.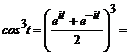
 =
= +
+  =
= 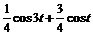 .
. .
.
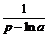 .
. ≓
≓  , Re p > α s 0. (3.1)
, Re p > α s 0. (3.1) .
. ≓
≓ 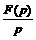 , Re р > s 0 (3.6)
, Re р > s 0 (3.6) является оригиналом, то
является оригиналом, то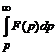 (3.9)
(3.9) . (3.10)
. (3.10) . (3.11)
. (3.11) (3.12)
(3.12)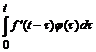 (3.13)
(3.13)
 (3.14)
(3.14)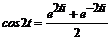 . Подставим его значение в заданную функцию, получим:
. Подставим его значение в заданную функцию, получим:  . Применив формулу (5) таблицы изображений функций, получим:
. Применив формулу (5) таблицы изображений функций, получим: = =
= = 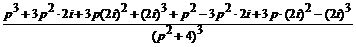 =
=
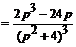 .
. . По теореме дифференцирования изображения (3.7): t × f 1 (t) ≓ - F ¢ (p), т. е.
. По теореме дифференцирования изображения (3.7): t × f 1 (t) ≓ - F ¢ (p), т. е.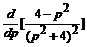 =
= =
=  .
. . Применив формулы (4-5) таблицы изображений функций, получим:
. Применив формулы (4-5) таблицы изображений функций, получим: ..
..


