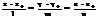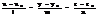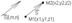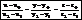Взаимное расположение плоскостей.
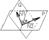
N1,N2-нормальные векторы плоскости.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
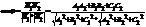
1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
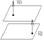
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
Нормированное уравнение плоскости. Отклонение и расстояние точки от плоскости.
Прямая в пространстве. Векторное, параметрическое, каноническое уравнение прямой.
Взаимное расположение двух прямых в пространстве. Теорема о скрещивающихся прямых и расстояние между ними.
Взаимное расположение прямой и плоскости.
P:A1x+B1y+C1z+D1=0^N1{A1,B1}
Q:A2x+B2y+C2z+D2=0^N2{A2,B2}
а)

то 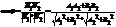
б)
 pq<=> N1||N2, то A1/A2=B1/B2
pq<=> N1||N2, то A1/A2=B1/B2
в)
 p||q<=> N1^N2, то A1A2+B1B2=0
p||q<=> N1^N2, то A1A2+B1B2=0
Поверхности вращения.
Поверхности вращения, поверхности, образуемые вращением плоской кривой вокруг прямой (оси П. в.), расположенной в плоскости этой линии.
Пусть в плоскости О yz задана кривая L уравнением: F (y; z)=0 (1)
Будем вращать эту кривую вокруг оси Оу. При вращении каждая точка кривой описывает окружность. Поверхность, полученная при вращении кривой, называется поверхностью вращения. Возьмем на линии L точку N(y, z). При
вращении вокруг оси О у точка N описывает
окружность. Возьмем на окружности точку
M(X, Y, Z), не принадлежащую плоскостям O yz и O xy. Пусть проекцией точки М на плоскость О ху будет точка K, а проекцией точки N на ось О у - точка P. Тогда MP=NР - радиус вращения точки N.




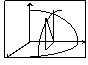
На рис.1 NP = z, MK = Z, РK = X, OP = Y.
Из прямоугольного треугольника MKP имеем
z=+-кв корень(X в 2 + Z в 2).
Кроме того, ордината точки M на окружности равна ординате точки N на кривой L, т. е. y= Y. Получим систему:
{z=+- кв корень(X в 2 + Z в 2); y= Y.
Если в уравнение (1) вместо y и z подставить их значения из системы, то получим:
F(Y; +- кв корень(X в 2 + Z в 2)=0
Таким образом, если линия F(y, z)= 0 расположена в плоскости O yz и вращается вокруг О у, для того,чтобы получить уравнение поверхности вращения,достаточно у заменить на Y, а вторую координату z заменить на
+- кв корень(X в 2 + Z в 2). Если, же задана линия на плоскости О ху: F(y, z)= 0 и вращение происходит вокруг оси О х, то уравнение поверхности вращения
имеет вид: F (X; +- кв корень(X в 2 + Z в 2)=0.
Исследовавание поверхностей второго порядка по их каноническим уравнениям.
Цилиндрические поверхности.
Цилиндрическая поверхность, поверхность, описываемая прямой линией (образующей Ц. п.), которая движется, оставаясь параллельной заданному направлению и скользя по заданной кривой (направляюще и). Если ось Oz прямоугольной системы координат параллельна образующей Ц. п., то уравнение Ц. п. будет F (x, у)= 0. Если образующие Ц. п. параллельны прямой ax + by + с = 0, лежащей в плоскости хОу, то уравнение Ц. п. имеет вид z = f (ax + by). Если направляющей служит окружность, эллипс, гипербола или парабола, то Ц. п. называется соответственно круглым, эллиптическим, гиперболическим или параболическим цилиндром.
Цилиндрическая поверхность задается в некоторой надлежаще выбранной
для данной поверхности канонической системе координат уравнением
F (x; y)= 0 (1) 
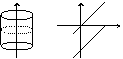
Кривая (1), определенная уравнением (1) в плоскости O xy, является направляющей кривой(основанием) цилиндрической поверхности. Образующая цилиндрической поверхности прямая параллельна оси O z (рис.1).Прямая M0 M - образующая. У точки
M(x0; y0; z) аппликата z может быть любой.
Например, если направляющей будет эллипс:
 , а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
, а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
О х. Тогда получается параболический цилиндр (рис.3).
Конические поверхности.
Определение. Поверхность называется конической, если она образована
перемещением в пространстве прямой (называемой образующей конической
поверхности), проходящей через одну и ту же точку M 0, называемую вершиной конической поверхности и пересекающей при этом некоторую линию L, называемую направляющей конической поверхности. Пусть в пространстве имеются две поверхности F 1 и F 2, которые, пересекаясь, образуют линию L. Уравнения этой линии определяются системой.
L: F 1(x; y; z)=0
F 2(x; y; z)=0
Зафиксируем точку M 0(x 0; y 0; z 0. Проведем прямую, проходящую через точку M 0 и какую-либо точку N (x 0; y 0; z 0) линии L. Если прямая M 0 N движется в пространстве так, что она проходит через точку M 0 - вершину конической поверхности и при этом пересекает линию L, то при этом образуется
коническая поверхность (рис. 1).
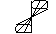
Обозначим координаты текущей точки конической поверхности через М(X;Y;Z). Составим уравнения прямой в пространстве, проходящей через точки M 0 и N. Точка поверхности M(X;Y;Z) принадлежит прямой M 0 N, определяемой уравнениями 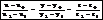
(2)
Если из уравнений (1) и (2) исключить x,y,z, то получится уравнение кони-
ческой поверхности: Ф(X; Y; Z)= 0. (3)
Плоскость в пространстве.
Ур-е в плоскости, проходящей через данную точку, перпендикулярно заданному вектору.
 N-вектор нормали
N-вектор нормали
M0M{x-x0,y-y0,z-z0}
Для того, чтобы точка MÎP, необходимо и достаточно чтобы вектора N^M0M(т.е. N*M0M=0)
A(x-x0)+B(y-y0)+С(z-z0)=0 - ур-е плоскости, проходящей через данную точку ^вектору.
Общее уравнение плоскости.
Ax+By+Сz-Ax0-By0-Сz0=0
-Ax0-By0-Сz0=D, где D=Ax+By+Сz
Ax+By+Сz+D=0
Частный случай:
Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)
Если A=0, то By+Сz+D=0
Если B=0, то Ax +Сz+D=0
Если C=0, то Ax+By+D=0
Если A=B=0, то Сz+D=0
Если A=C=0, то By+D=0
Если A=D=0, то By+Сz=0
Если B=D=0, то Ay+Сz=0
 12. Каноническое уравнение прямой в пространстве.
12. Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
 Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
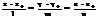
13. Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.
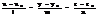
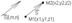
l m n
S{x2-x1,y2-y1,z2-z1}
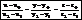




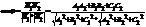


 pq<=> N1||N2, то A1/A2=B1/B2
pq<=> N1||N2, то A1/A2=B1/B2 p||q<=> N1^N2, то A1A2+B1B2=0
p||q<=> N1^N2, то A1A2+B1B2=0




 , а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
, а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
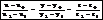
 N-вектор нормали
N-вектор нормали 12. Каноническое уравнение прямой в пространстве.
12. Каноническое уравнение прямой в пространстве. Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S