Определитель квадратной матрицы.
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Определитель квадратной матрицы
 –число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками “+” и “–” по некоторому определенному правилу.
–число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками “+” и “–” по некоторому определенному правилу.
Сомножители в каждом слагаемом записываются в порядке следования строк, тогда номера столбцов образуют перестановки. Слагаемые, соответствующие четным перестановкам, берутся со знаком “+”, соответствующие нечетным – со знаком “–”. Для некоторой перестановки чисел 1, 2, …,  –
–  пара элементов
пара элементов  ,
, 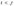 образует инверсию, если
образует инверсию, если  . Если число пар элементов перестановки, образующих инверсию, четное, то перестановка четная, иначе – нечетная.
. Если число пар элементов перестановки, образующих инверсию, четное, то перестановка четная, иначе – нечетная.
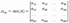
Определитель для случая  .
. 
Определитель для случая  .
. 
Определитель для случая  .
.

При вычислении определителя матрицы размерности 3 получаются следующие слагаемые суммы, перестановки индексов столбцов, инверсии и знаки слагаемых. 
Таким образом, определитель вычисляется по следующей формуле: 
Свойства определителей:
1. При транспонировании матрицы её определитель не меняется.
2. При перестановке двух строк определителя, он меняет свой знак, но по абсолютной величине не меняется.
3. При умножении определителя на число, достаточно умножить любую строку на это число.
4. Если определитель содержит нулевую строку, то он равен нулю.
5. Свойство упрощения определителя:
Определитель не изменяется, если к элементам любой его строки прибавить элементы любой другой его строки, предварительно умножив их на одно и тоже любое число.
6. Сумма определителей, отличающихся одной строкой, равна определителю с теми же элементами, у которого вместо различных строк стоит строка из суммы элементов различных строк.
7. Если определитель имеет две пропорциональные строки, то он равен нулю.
8. Сумма попарных произведений элементов кокой либо строки и алгебраических дополнений соответствующих элементов другой строки равна нулю.
9. Определитель произведения двух квадратных матриц равен произведению их определителей.
10. Определитель треугольной матрицы равен произведению своих диагональных элементов.
Алгебраическое дополнение.
Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Минором матрицы порядка к называют определитель  , составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы.
, составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы. 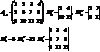
Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.
Рангом матрицы называется число ненулевых строк в ее ступенчатом виде.
Ранг матрицы A обозначается r(A) = rang(A). Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду.Пример. Найти ранг матрицы:

Решение. Приведем матрицу A к ступенчатому виду.
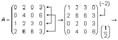
 .
.
Ранг матрицы A равен двум, r(A) = rang(A). В любой матрице A с рангом r(А) = k найдутся такие k строки, что ранг матрицы, составленной их этих строк, также равен k. Такие строки матрицы A называются базисными. Если при приведении матрицы A к ступенчатому виду не использовать прибавление какой-либо строки низшей, чем данная, то базисные строки матрицы A — это в точности те строки, которые при приведении к ступенчатому виду перешли в ненулевые строки. Найдем базисные строки матрицы в последнем примере. Для этого будем отмечать ненулевые строки слева, начиная с последней матрицы (ступенчатого вида матрицы A). Затем отметим соответствующие им строки у каждой матрицы, учитывая изменение положения строк (элементарные преобразования 1-го типа). У матрицы A базисные строки 3-я и 4-я.
5.Правило Крамера. Если определитель матрицы коэффициентов системы с одинаковым количеством уравнений и неизвестных не равен нулю, то эта система имеет единственное решение, которое может быть найдено с помощью определителей по формуле:
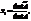 где
где 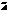 – матрица, получаемая путём замены i ого столбца на столбец свободных членов. Доказательство:
– матрица, получаемая путём замены i ого столбца на столбец свободных членов. Доказательство: 
Если количество неизвестных не равно количеству уравнений, или определитель матрицы коэффициентов равен нулю, то правило Крамара не применяется.
6.Теорема Кронекера-Капели:
Система совместна, если ранг расширенной матрицы равен рангу матрицы коэффициентов.
Доказательство:
Необходимое условие:
Если система совместна, то ранг расширенной матрицы и ранг матрицы коэффициентов равны. 
Следовательно, столбец свободных членов линейно зависит от столбцов матрицы коэффициентов, поэтом столбцы расширенной матрицы содержат тоже количество независимых столбцов, что и матрица коэффициентов, тогда добавление линейно зависимого столбца не изменит ранг матрицы. Следовательно, по теореме о ранге матрицы, ранг матрицы коэффициентов равен рангу расширенной матрицы.
Достаточное условие:
Применим правило Крамара к произвольной системе.
Пусть система  совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
Назовём базисными те переменные, которые входят в базисный минор, а все остальные – свободными.
Тогда по теореме о базисном миноре нижние строки расширенной матрицы являются линейно зависимыми от первых строк, то есть могут быть представлены, как их линейные комбинации, следовательно, они являются лишними и могут быть отброшены. В результате остаётся система с r уравнениями и тем же количеством неизвестных, где r – ранг системы, или ранг базисного минора.
Действия над векторами.
а=х1i+y1j+z1k; b=х2i+y2j+z2k
l*a=l(х1i+y1j+z1k)= l(х1)i+l (y1)j+l(z1)k
a±b=(x1±x2)i+(y1±y2)j+(z1±z2)k
ab=x1x2ii+y1x2ij+x2z1ki+x1y2ij+y1y2jj+ z1y2kj+x1z1ik+y1z2jk+z1z2kk=x1x2+y1y2+z1z2
ii=1; ij=0; и т.д.
скалярное произведение 2х векторов равно сумме произведений соответствующих координат этих векторов.
аа=x2+y2+z2=|a|2 a{x,y,z}, aa=|a|*|a|, то a2=|a|2

ab=|a|*|b|*cosj
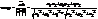
а)ав=0,<=>а^в, x1x2+y1y2+z1z2=0
б)а||в - коллинеарны, если, x1/x2=y1/y2=z1/z2
11.Понятие вектора. Линейная зависимость и независимость системы векторов и связанные с этими понятиями теоремы. Коллинеарные и компланарные вектора.
Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3.
Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
Гипербола и ее св-ва.
Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2+Cy2=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0
б) Если d>0, то каноническое ур-е гиперболы примет вид: x2/a2-y2/b2=1, F1(c,o) и F2(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.
Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.
б) если d=0, ур-е примет вид x2/a2-y2/b2=0, получаем 2 перекрестные прямые х/а±у/b=0
в) если d<0, то x2/a2-y2/b2=-1 - ур-е сопряженной гиперболы.
Парабола и ее свойства.
Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз. параболой.
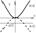 Если вершина нах. в О(0,0), то ур-е примет вид
Если вершина нах. в О(0,0), то ур-е примет вид
y2=2px-симметрично отн. оси ОХ
х2=2pу-симметрично отн. оси ОУ
Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.
Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2
Св-ва:
1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2.
Поверхности вращения.
Поверхности вращения, поверхности, образуемые вращением плоской кривой вокруг прямой (оси П. в.), расположенной в плоскости этой линии.
Пусть в плоскости О yz задана кривая L уравнением: F (y; z)=0 (1)
Будем вращать эту кривую вокруг оси Оу. При вращении каждая точка кривой описывает окружность. Поверхность, полученная при вращении кривой, называется поверхностью вращения. Возьмем на линии L точку N(y, z). При
вращении вокруг оси О у точка N описывает
окружность. Возьмем на окружности точку
M(X, Y, Z), не принадлежащую плоскостям O yz и O xy. Пусть проекцией точки М на плоскость О ху будет точка K, а проекцией точки N на ось О у - точка P. Тогда MP=NР - радиус вращения точки N.




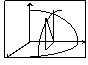
На рис.1 NP = z, MK = Z, РK = X, OP = Y.
Из прямоугольного треугольника MKP имеем
z=+-кв корень(X в 2 + Z в 2).
Кроме того, ордината точки M на окружности равна ординате точки N на кривой L, т. е. y= Y. Получим систему:
{z=+- кв корень(X в 2 + Z в 2); y= Y.
Если в уравнение (1) вместо y и z подставить их значения из системы, то получим:
F(Y; +- кв корень(X в 2 + Z в 2)=0
Таким образом, если линия F(y, z)= 0 расположена в плоскости O yz и вращается вокруг О у, для того,чтобы получить уравнение поверхности вращения,достаточно у заменить на Y, а вторую координату z заменить на
+- кв корень(X в 2 + Z в 2). Если, же задана линия на плоскости О ху: F(y, z)= 0 и вращение происходит вокруг оси О х, то уравнение поверхности вращения
имеет вид: F (X; +- кв корень(X в 2 + Z в 2)=0.
Цилиндрические поверхности.
Цилиндрическая поверхность, поверхность, описываемая прямой линией (образующей Ц. п.), которая движется, оставаясь параллельной заданному направлению и скользя по заданной кривой (направляюще и). Если ось Oz прямоугольной системы координат параллельна образующей Ц. п., то уравнение Ц. п. будет F (x, у)= 0. Если образующие Ц. п. параллельны прямой ax + by + с = 0, лежащей в плоскости хОу, то уравнение Ц. п. имеет вид z = f (ax + by). Если направляющей служит окружность, эллипс, гипербола или парабола, то Ц. п. называется соответственно круглым, эллиптическим, гиперболическим или параболическим цилиндром.
Цилиндрическая поверхность задается в некоторой надлежаще выбранной
для данной поверхности канонической системе координат уравнением
F (x; y)= 0 (1) 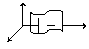
Кривая (1), определенная уравнением (1) в плоскости O xy, является направляющей кривой(основанием) цилиндрической поверхности. Образующая цилиндрической поверхности прямая параллельна оси O z (рис.1).Прямая M0 M - образующая. У точки
M(x0; y0; z) аппликата z может быть любой.
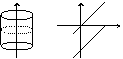
Например, если направляющей будет эллипс:
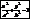 , а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
, а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
О х. Тогда получается параболический цилиндр (рис.3).
Конические поверхности.
Определение. Поверхность называется конической, если она образована
перемещением в пространстве прямой (называемой образующей конической
поверхности), проходящей через одну и ту же точку M 0, называемую вершиной конической поверхности и пересекающей при этом некоторую линию L, называемую направляющей конической поверхности. Пусть в пространстве имеются две поверхности F 1 и F 2, которые, пересекаясь, образуют линию L. Уравнения этой линии определяются системой.
L: F 1(x; y; z)=0
F 2(x; y; z)=0
Зафиксируем точку M 0(x 0; y 0; z 0. Проведем прямую, проходящую через точку M 0 и какую-либо точку N (x 0; y 0; z 0) линии L. Если прямая M 0 N движется в пространстве так, что она проходит через точку M 0 - вершину конической поверхности и при этом пересекает линию L, то при этом образуется
коническая поверхность (рис. 1).
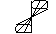
Обозначим координаты текущей точки конической поверхности через М(X;Y;Z). Составим уравнения прямой в пространстве, проходящей через точки M 0 и N. Точка поверхности M(X;Y;Z) принадлежит прямой M 0 N, определяемой уравнениями 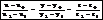
(2)
Если из уравнений (1) и (2) исключить x,y,z, то получится уравнение кони-
ческой поверхности: Ф(X; Y; Z)= 0. (3)
Плоскость в пространстве.
Ур-е в плоскости, проходящей через данную точку, перпендикулярно заданному вектору.
 N-вектор нормали
N-вектор нормали
M0M{x-x0,y-y0,z-z0}
Для того, чтобы точка MÎP, необходимо и достаточно чтобы вектора N^M0M(т.е. N*M0M=0)
A(x-x0)+B(y-y0)+С(z-z0)=0 - ур-е плоскости, проходящей через данную точку ^вектору.
Общее уравнение плоскости.
Ax+By+Сz-Ax0-By0-Сz0=0
-Ax0-By0-Сz0=D, где D=Ax+By+Сz
Ax+By+Сz+D=0
Частный случай:
Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)
Если A=0, то By+Сz+D=0
Если B=0, то Ax +Сz+D=0
Если C=0, то Ax+By+D=0
Если A=B=0, то Сz+D=0
Если A=C=0, то By+D=0
Если A=D=0, то By+Сz=0
Если B=D=0, то Ay+Сz=0
 12. Каноническое уравнение прямой в пространстве.
12. Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
 Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
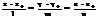
13. Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.
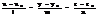
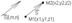
l m n
S{x2-x1,y2-y1,z2-z1}
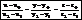
Кривые линии 2-го порядка.
Кривые 2го порядка описываются с помощью общего ур-я:
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где

а) Каноническое ур-е эллипса
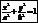 - Каноническое ур-е эллипса
- Каноническое ур-е эллипса
Если a=b, то x2+b2=a2 - ур-е окружности.
б) Ур-е гиперболы: x2/a2-y2/b2=1

в) ур-е параболы: y2=2px или y=ax2
г) ур-е сферы: x2+y2+z2=а2 (r2=(x-a)2+(y-b)2+(z-c)2)
д) ур-е эллипса: x2/a2-y2/b2+z2/c2=1
Определитель квадратной матрицы.
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Определитель квадратной матрицы
 –число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками “+” и “–” по некоторому определенному правилу.
–число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками “+” и “–” по некоторому определенному правилу.
Сомножители в каждом слагаемом записываются в порядке следования строк, тогда номера столбцов образуют перестановки. Слагаемые, соответствующие четным перестановкам, берутся со знаком “+”, соответствующие нечетным – со знаком “–”. Для некоторой перестановки чисел 1, 2, …,  –
–  пара элементов
пара элементов  ,
, 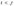 образует инверсию, если
образует инверсию, если  . Если число пар элементов перестановки, образующих инверсию, четное, то перестановка четная, иначе – нечетная.
. Если число пар элементов перестановки, образующих инверсию, четное, то перестановка четная, иначе – нечетная.
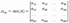
Определитель для случая  .
. 
Определитель для случая  .
. 
Определитель для случая  .
.

При вычислении определителя матрицы размерности 3 получаются следующие слагаемые суммы, перестановки индексов столбцов, инверсии и знаки слагаемых. 
Таким образом, определитель вычисляется по следующей формуле: 
Свойства определителей:
1. При транспонировании матрицы её определитель не меняется.
2. При перестановке двух строк определителя, он меняет свой знак, но по абсолютной величине не меняется.
3. При умножении определителя на число, достаточно умножить любую строку на это число.
4. Если определитель содержит нулевую строку, то он равен нулю.
5. Свойство упрощения определителя:
Определитель не изменяется, если к элементам любой его строки прибавить элементы любой другой его строки, предварительно умножив их на одно и тоже любое число.
6. Сумма определителей, отличающихся одной строкой, равна определителю с теми же элементами, у которого вместо различных строк стоит строка из суммы элементов различных строк.
7. Если определитель имеет две пропорциональные строки, то он равен нулю.
8. Сумма попарных произведений элементов кокой либо строки и алгебраических дополнений соответствующих элементов другой строки равна нулю.
9. Определитель произведения двух квадратных матриц равен произведению их определителей.
10. Определитель треугольной матрицы равен произведению своих диагональных элементов.
Алгебраическое дополнение.
Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Минором матрицы порядка к называют определитель  , составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы.
, составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы. 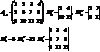
Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.
Рангом матрицы называется число ненулевых строк в ее ступенчатом виде.
Ранг матрицы A обозначается r(A) = rang(A). Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду.Пример. Найти ранг матрицы:

Решение. Приведем матрицу A к ступенчатому виду.

 .
.
Ранг матрицы A равен двум, r(A) = rang(A). В любой матрице A с рангом r(А) = k найдутся такие k строки, что ранг матрицы, составленной их этих строк, также равен k. Такие строки матрицы A называются базисными. Если при приведении матрицы A к ступенчатому виду не использовать прибавление какой-либо строки низшей, чем данная, то базисные строки матрицы A — это в точности те строки, которые при приведении к ступенчатому виду перешли в ненулевые строки. Найдем базисные строки матрицы в последнем примере. Для этого будем отмечать ненулевые строки слева, начиная с последней матрицы (ступенчатого вида матрицы A). Затем отметим соответствующие им строки у каждой матрицы, учитывая изменение положения строк (элементарные преобразования 1-го типа). У матрицы A базисные строки 3-я и 4-я.
5.Правило Крамера. Если определитель матрицы коэффициентов системы с одинаковым количеством уравнений и неизвестных не равен нулю, то эта система имеет единственное решение, которое может быть найдено с помощью определителей по формуле:
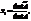 где
где 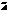 – матрица, получаемая путём замены i ого столбца на столбец свободных членов. Доказательство:
– матрица, получаемая путём замены i ого столбца на столбец свободных членов. Доказательство: 
Если количество неизвестных не равно количеству уравнений, или определитель матрицы коэффициентов равен нулю, то правило Крамара не применяется.
6.Теорема Кронекера-Капели:
Система совместна, если ранг расширенной матрицы равен рангу матрицы коэффициентов.
Доказательство:
Необходимое условие:
Если система совместна, то ранг расширенной матрицы и ранг матрицы коэффициентов равны. 
Следовательно, столбец свободных членов линейно зависит от столбцов матрицы коэффициентов, поэтом столбцы расширенной матрицы содержат тоже количество независимых столбцов, что и матрица коэффициентов, тогда добавление линейно зависимого столбца не изменит ранг матрицы. Следовательно, по теореме о ранге матрицы, ранг матрицы коэффициентов равен рангу расширенной матрицы.
Достаточное условие:
Применим правило Крамара к произвольной системе.
Пусть система  совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
Назовём базисными те переменные, которые входят в базисный минор, а все остальные – свободными.
Тогда по теореме о базисном миноре нижние строки расширенной матрицы являются линейно зависимыми от первых строк, то есть могут быть представлены, как их линейные комбинации, следовательно, они являются лишними и могут быть отброшены. В результате остаётся система с r уравнениями и тем же количеством неизвестных, где r – ранг системы, или ранг базисного минора.



 –число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками “+” и “–” по некоторому определенному правилу.
–число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками “+” и “–” по некоторому определенному правилу. –
–  пара элементов
пара элементов  ,
, 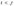 образует инверсию, если
образует инверсию, если  . Если число пар элементов перестановки, образующих инверсию, четное, то перестановка четная, иначе – нечетная.
. Если число пар элементов перестановки, образующих инверсию, четное, то перестановка четная, иначе – нечетная.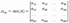
 .
. 
 .
. 
 .
.


 , составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы.
, составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы. 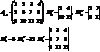


 .
.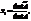 где
где 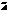 – матрица, получаемая путём замены i ого столбца на столбец свободных членов. Доказательство:
– матрица, получаемая путём замены i ого столбца на столбец свободных членов. Доказательство: 

 совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
совместна, тогда ранг расширенной матрицы равен рангу матрицы коэффициентов, тогда переставим уравнения системы, и перенумеруем переменные так, что бы базисный минор стоял в левом верхнем углу.
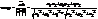
 Если вершина нах. в О(0,0), то ур-е примет вид
Если вершина нах. в О(0,0), то ур-е примет вид




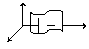
 , а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
, а образующая параллельна оси O z, то получится эллиптический цилиндр (рис. 2).Пусть направляющей будет парабола y= z в кв, а образующая параллельна оси
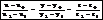
 N-вектор нормали
N-вектор нормали 12. Каноническое уравнение прямой в пространстве.
12. Каноническое уравнение прямой в пространстве. Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S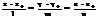
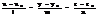
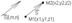
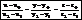

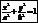 - Каноническое ур-е эллипса
- Каноническое ур-е эллипса



