Нормальные напряжения в поперечных сечениях. При центральном растяжении (сжатии) стержней в их поперечных сечениях действует только одно внутреннее усилие – продольная сила N.
Поэтому в этих сечениях будут возникать только нормальные напряжения 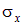 . Поскольку других нормальных напряжений в поперечных сечениях нет, будем в дальнейшем опускать индекс у напряжения, обозначая
. Поскольку других нормальных напряжений в поперечных сечениях нет, будем в дальнейшем опускать индекс у напряжения, обозначая 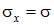 .
.
В соответствии с гипотезой плоских сечений сечения, плоские и перпендикулярные оси стержня до деформации, остаются плоскими и перпендикулярными оси после деформации.
Можно показать, что применение этой гипотезы приводит к простой формуле для определения нормальных напряжений при растяжении и сжатии.
|
| 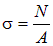 . .
| (2.5)
|
Эти напряжения постоянны по сечению (рис. 2.5)
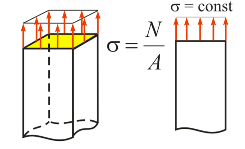
Рис 2.5. Распределение нормальных напряжений по сечению при растяжении
При известной эпюре продольных сил формула (2.5) позволяет довольно просто построить эпюру  . Для этого необходимо в характерных сечениях разделить значение силы N на площадь поперечного сечения А. Если площадь постоянна по длине стержня, эпюра
. Для этого необходимо в характерных сечениях разделить значение силы N на площадь поперечного сечения А. Если площадь постоянна по длине стержня, эпюра 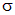 будет полностью подобна эпюре N.
будет полностью подобна эпюре N.
Напряжения на наклонных площадках. Рассмотрим элемент стержня, образованный поперечным и наклонным к оси стержня сечениями (рис. 2.7, а). Стержень растягивается силами F по его концам.
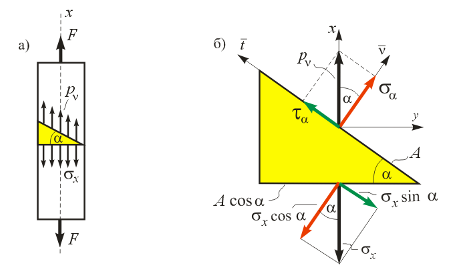
Рис 2.7. Напряжения на наклонных площадках
Обозначим площадь наклонного сечения А, тогда площадь горизонтальной площадки будет равна А × соs α (рис. 2.7,б), где α – угол поворота нормали наклонного сечения относительно оси х. Очевидно, что продольная сила равна N = F = s х × (А соs α) = p n А и постоянна по длине стержня. Поэтому полные напряжения p n = s х соs α.
Разложим вектор полного напряжения p n на две составляющие sα и t α и составим два уравнения равновесия 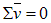 и
и 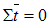 для выделенного треугольного элемента.
для выделенного треугольного элемента.
|
| 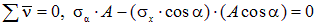 ; ;

| (2.6)
|
Обозначая s x = s, из этих уравнений найдем
|
| 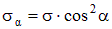 ; ;
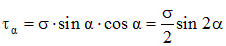 . .
| (2.7)
|
Из равенств (2.7) видно, что sa и ta являются периодическими функциями, зависящими от угла a наклона сечения. При различных углах a:
а) a = 0 (поперечное сечение); sa = s; ta = 0;
б) a = 90° (продольное сечение); sa = 0; ta = 0;
в) a = 45° (наклонное под углом 45° сечение); sa = s /2; ta = s/2.
Из второго равенства (2.7) можно установить, что касательные напряжения достигают максимума на площадках, наклоненных к поперечному сечению под углом 45 ° (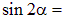 sin 90° = 1) и равны половине значения нормальных напряжений в поперечном сечении:
sin 90° = 1) и равны половине значения нормальных напряжений в поперечном сечении:
|
| 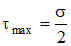 . .
| (2.8)
|
Максимальные нормальные напряжения возникают в поперечных сечениях и определяются по формуле (2.5).
Деформации. Рассмотрим деформированное состояние стержней при растяжении и сжатии. При растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот. Это легко наблюдать в опытах с резиновыми образцами, в которых деформации достаточно велики.
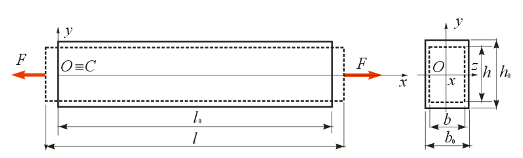
Рис 2.8. Деформирование стержня при растяжении
Рассмотрим, какие деформации возникают при растяжении стержня (рис. 2.8).
Величина D l = l – l 0 называется абсолютным удлинением, или абсолютной линейной продольной деформацией стержня (здесь l 0 – первоначальная длина, а l – длина после деформации). Величины D h = h – h0 и D b= b – b0 называются абсолютными линейными поперечными деформациями (здесь h 0 и b 0 – первоначальные поперечные размеры, h и b – поперечные размеры после деформации). Абсолютные деформации измеряются в единицах длины (метрах, сантиметрах, миллиметрах).
Если разделить величины абсолютных деформаций на первоначальные размеры, то получим величины, называемые относительными линейными деформациями. Согласно принятым ранее обозначениям осей координат (х – вдоль оси стержня, а y и z – в поперечном сечении), относительные продольные деформации будут обозначаться 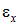 , а относительные поперечные деформации –
, а относительные поперечные деформации – 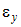 и
и 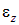 . Продольную и поперечные относительные деформации можно определить по формулам:
. Продольную и поперечные относительные деформации можно определить по формулам:
Учитывая, что 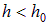 ,
, 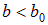 , можно заметить, что при растяжении стержня поперечные деформации будут отрицательными. Для изотропных материалов
, можно заметить, что при растяжении стержня поперечные деформации будут отрицательными. Для изотропных материалов 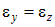 . Из многочисленных опытов установлено, что отношение поперечных деформаций к продольным для каждого конкретного материала является постоянной величиной:
. Из многочисленных опытов установлено, что отношение поперечных деформаций к продольным для каждого конкретного материала является постоянной величиной:
|
| 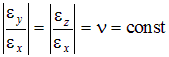 . .
| (2.10)
|
Константа 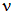 называется коэффициентом поперечной деформации, или коэффициентом Пуассона и является одной из двух упругих характеристик материала (постоянных упругости). Очевидно, что коэффициент Пуассона является безразмерной величиной. Значения
называется коэффициентом поперечной деформации, или коэффициентом Пуассона и является одной из двух упругих характеристик материала (постоянных упругости). Очевидно, что коэффициент Пуассона является безразмерной величиной. Значения 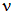 для некоторых материалов приведены в табл. 2.1. Для всех материалов величина
для некоторых материалов приведены в табл. 2.1. Для всех материалов величина 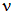 лежит в пределах от 0 до 0,5. Материал, у которого
лежит в пределах от 0 до 0,5. Материал, у которого 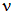 = 0,5, называется несжимаемым. Таким материалом, у которого
= 0,5, называется несжимаемым. Таким материалом, у которого 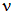 = 0,5, является резина на основе натурального каучука. Материал, имеющий
= 0,5, является резина на основе натурального каучука. Материал, имеющий 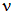 = 0, – это, например, кора пробкового дерева.
= 0, – это, например, кора пробкового дерева.
Учитывая, что продольные и поперечные деформации имеют разный знак, будет справедливым следующее выражение:
|
| 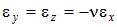 . .
| (2.11)
|
Обозначая e x = e, e y = e z = e¢, формулу для определения коэффициента Пуассона можно переписать в часто встречающемся в учебниках по сопротивлению материалов виде:
|
| 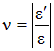 . .
| (2.12)
|
Закон Гука. Связь между напряжениями и деформациями была установлена экспериментально в 1676 г. английским ученым Робертом Гуком Эта связь в случае одноосного растяжения (сжатия) имеет вид
|
| 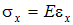 . .
| (2.13)
|
и называется законом Гука. Для краткости можно опустить индексы и записать закон Гука в виде
|
| 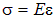 или или 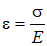 . .
| (2.14)
|
Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости, или модулем Юнга. Модуль упругости является второй упругой характеристикой материалов после коэффициента Пуассона и характеризует важное их свойство – жесткость. Чем больше Е, тем более жесткий материал мы имеем.
Учитывая, что линейные деформации являются безразмерными величинами, можно заключить, что размерность модуля упругости такая же, как и у напряжений (МПа).
График зависимости s(e) представляет собой прямую линию, выходящую из начала координат (рис. 2.9). Графическая интерпретация модуля упругости на этом рисунке часто обозначается как тангенс угла наклона прямой к оси 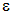 . Однако следует заметить, что запись
. Однако следует заметить, что запись 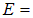 tg
tg 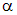 следует воспринимать условно, так как размерность у модуля упругости – МПа, а тангенс – безразмерная величина.
следует воспринимать условно, так как размерность у модуля упругости – МПа, а тангенс – безразмерная величина.

Рис 2.9. Графическое изображение закона Гука
Значения модуля Юнга для разных материалов лежат в очень широких пределах. Например, для резины он равен 1–10 МПа, а для стали – больше 2·105 МПа. В табл. 2.1 приведены примерные значения Е для некоторых материалов.
Таблица 2.1
Модули упругости Е и коэффициенты Пуассона ν
(примерные величины)
| Материал
| Е, МПа
| ν
|
| Сталь
| » 2·105
| » 0,3
|
| Алюминий, медь
| » 1 ·105
| » 0,3
|
| Бетон
| » 2·104
| » 0,15
|
| Кирпичная кладка
| » 3·103
| » 0,2
|
| Дерево
| » 1·104 вдоль волокон
» 400 поперек волокон
| » 0,45
|
| Резина на основе
каучука
| »10
| 0,5
|
| Пробковая кора
| »5
| 0
|



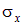 . Поскольку других нормальных напряжений в поперечных сечениях нет, будем в дальнейшем опускать индекс у напряжения, обозначая
. Поскольку других нормальных напряжений в поперечных сечениях нет, будем в дальнейшем опускать индекс у напряжения, обозначая 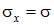 .
.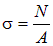 .
.

 . Для этого необходимо в характерных сечениях разделить значение силы N на площадь поперечного сечения А. Если площадь постоянна по длине стержня, эпюра
. Для этого необходимо в характерных сечениях разделить значение силы N на площадь поперечного сечения А. Если площадь постоянна по длине стержня, эпюра 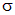 будет полностью подобна эпюре N.
будет полностью подобна эпюре N.
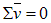 и
и 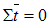 для выделенного треугольного элемента.
для выделенного треугольного элемента.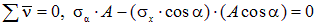 ;
;

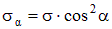 ;
;
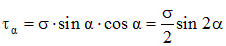 .
.
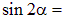 sin 90° = 1) и равны половине значения нормальных напряжений в поперечном сечении:
sin 90° = 1) и равны половине значения нормальных напряжений в поперечном сечении: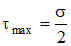 .
.

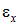 , а относительные поперечные деформации –
, а относительные поперечные деформации – 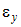 и
и 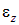 . Продольную и поперечные относительные деформации можно определить по формулам:
. Продольную и поперечные относительные деформации можно определить по формулам: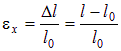 ;
;
 ;
;
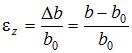 .
.
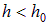 ,
, 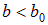 , можно заметить, что при растяжении стержня поперечные деформации будут отрицательными. Для изотропных материалов
, можно заметить, что при растяжении стержня поперечные деформации будут отрицательными. Для изотропных материалов 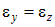 . Из многочисленных опытов установлено, что отношение поперечных деформаций к продольным для каждого конкретного материала является постоянной величиной:
. Из многочисленных опытов установлено, что отношение поперечных деформаций к продольным для каждого конкретного материала является постоянной величиной: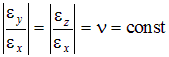 .
.
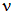 называется коэффициентом поперечной деформации, или коэффициентом Пуассона и является одной из двух упругих характеристик материала (постоянных упругости). Очевидно, что коэффициент Пуассона является безразмерной величиной. Значения
называется коэффициентом поперечной деформации, или коэффициентом Пуассона и является одной из двух упругих характеристик материала (постоянных упругости). Очевидно, что коэффициент Пуассона является безразмерной величиной. Значения 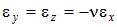 .
.
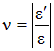 .
.
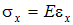 .
.
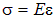 или
или 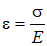 .
.
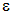 . Однако следует заметить, что запись
. Однако следует заметить, что запись 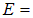 tg
tg 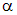 следует воспринимать условно, так как размерность у модуля упругости – МПа, а тангенс – безразмерная величина.
следует воспринимать условно, так как размерность у модуля упругости – МПа, а тангенс – безразмерная величина.



