СВОЙСТВО: Если 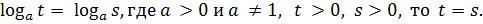
(указанное свойство действует и в обратном направлении).
На основании этого свойства можно сформулировать следующее утверждение
ТЕОРЕМА: Если f(x) > 0 и g(x) > 0, то логарифмическое уравнение
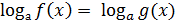 (а > 0 и а
(а > 0 и а 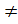 1) равносильно уравнению f(x) = g(x).
1) равносильно уравнению f(x) = g(x).
ПРИМЕР. Уравнение 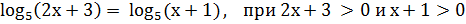
равносильно уравнению 2х + 3 = х + 1.
Методы решения логарифмических уравнений
Методы решения логарифмических уравнений:
1. по определению логарифма и его свойствам;
2. метод потенциирования (на основе теоремы: переход от уравнения 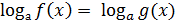 к уравнению вида f(x) = g(x));
к уравнению вида f(x) = g(x));
3. введение новой переменной;
4. логарифмирование обеих частей уравнения;
5. использование специальной формулы;
6. функционально – графический.
Этапы решения логарифмических уравнений:
1. запись условия и нахождение ОДЗ уравнения;
2. выбор метода решения уравнения;
3. решение уравнения;
4. проверка корней с помощью ОДЗ;
5. запись ответа, исключив из него посторонние корни (не удовлетворяющие ОДЗ).
Рассмотрим примеры решения логарифмических уравнений на основе первых четырех методов с помощью этапов решения уравнений.
ПРИМЕР. Решить уравнение 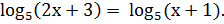
Этап: запись условия и нахождение ОДЗ
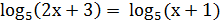
Это уравнение определено для значений х,
удовлетворяющих неравенствам:
ОДЗ: 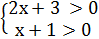
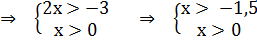
- 1,5 0
Получаем ОДЗ: х 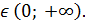
Этап: выбор метода решения уравнения
Т.к. уравнение имеет вид 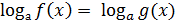 , то для его решения целесообразно выбрать метод потенциирования.
, то для его решения целесообразно выбрать метод потенциирования.
Этап: решение уравнения
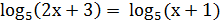 ; по теореме получаем
; по теореме получаем
2х +3 = х + 1;
2х – х = 1 – 3;
х = - 2.
Этап: проверка корней с помощью ОДЗ
Число - 2 не принадлежит промежутку 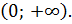 Значит – 2 не удовлетворяет ОДЗ.
Значит – 2 не удовлетворяет ОДЗ.
Этап: запись ответа, исключив из него посторонние корни
(не удовлетворяющие ОДЗ).
Ответ: корней нет.
ПРИМЕР. Решить уравнение 
lg – «десятичный логарифм» (основание логарифма равно 10)
 ОДЗ:
ОДЗ: 
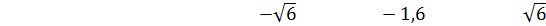
ОДЗ: 

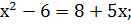
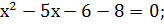

D = 25 - 4∙ (-14) = 81;
х1 = 7 и х2 = - 2 - не удовлетворяет ОДЗ
Ответ: х = 7.
ПРИМЕР. Решить уравнение 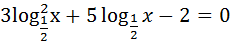 .
.
Этап: запись условия и нахождение ОДЗ
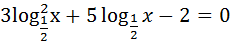 ; ОДЗ: х > 0.
; ОДЗ: х > 0.
Этап: выбор метода решения уравнения
Для решения данного уравнения не подходит метод потенциирования, т. к. уравнение не имеет вид 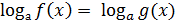 . Определение логарифма и его свойства мы тоже применить не можем. Поэтому целесообразно применить метод введения новой переменной.
. Определение логарифма и его свойства мы тоже применить не можем. Поэтому целесообразно применить метод введения новой переменной.
Этап: решение уравнения
t = 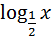
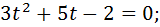
D = 25 – 4 ∙ 3 ∙ (-2) = 49;
t1 =  и t2 = - 2
и t2 = - 2
возвращаемся к переменной х
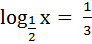
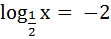
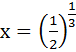
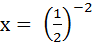
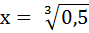
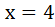
Этап: проверка корней с помощью ОДЗ
Корни удовлетворяю ОДЗ.
Этап: запись ответа, исключив из него посторонние корни
(не удовлетворяющие ОДЗ).
Ответ: 4 и  .
.
ПРИМЕР. Решить уравнение  .
.
ОДЗ:  ⇒
⇒ 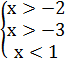
- 3 - 2 1


По свойству: 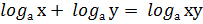 получаем:
получаем:

По теореме получаем:
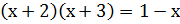 ;
;
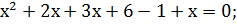
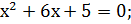

Ответ: - 1.
ПРИМЕР. Решить уравнение 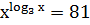 .
.
Этап: запись условия и нахождение ОДЗ
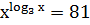 ОДЗ: х > 0 и х ≠ 1
ОДЗ: х > 0 и х ≠ 1
Этап: выбор метода решения уравнения
Логарифмируем обе части уравнения по основанию 3 по свойству: если х = у, то 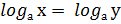 .
.
Этап: решение уравнения
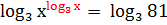 ;
;
По свойству 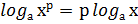 получаем:
получаем:
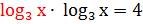 ;
;
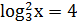 - уравнение вида
- уравнение вида 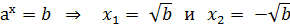
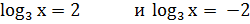
По определению логарифма:
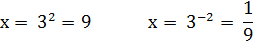
Этап: проверка корней с помощью ОДЗ
Корни удовлетворяю ОДЗ.
Этап: запись ответа, исключив из него посторонние корни
(не удовлетворяющие ОДЗ).
Ответ:  и 9.
и 9.
ПРИМЕР. Решить уравнение  .
.



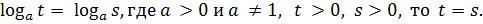
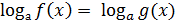 (а > 0 и а
(а > 0 и а 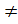 1) равносильно уравнению f(x) = g(x).
1) равносильно уравнению f(x) = g(x).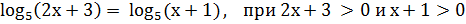
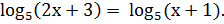
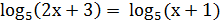
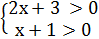
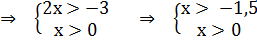

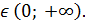
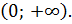 Значит – 2 не удовлетворяет ОДЗ.
Значит – 2 не удовлетворяет ОДЗ.



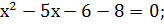

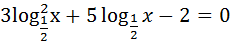 .
.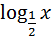
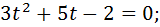
 и t2 = - 2
и t2 = - 2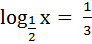
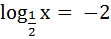
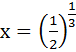
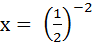
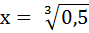
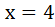
 .
. .
. ⇒
⇒ 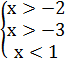


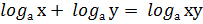 получаем:
получаем:
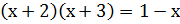 ;
;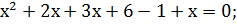
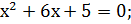

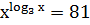 .
.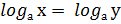 .
.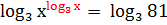 ;
;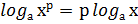 получаем:
получаем: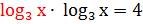 ;
;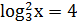 - уравнение вида
- уравнение вида 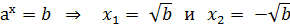
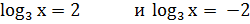
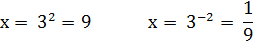
 и 9.
и 9. .
.


