

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Многополярность имеет дело со сложными поляризованными функциями так, что после взятия производной, а затем интегрирования, функции должна вернуть свой исходный вид. Начнём с не сложных примеров. Дана функция с несколькими переменными, но чётко каждая переменная находится в своей полярной плоскости: f(w) = 4х2 + 2iy + 3jg, здесь x, y, g – переменные.
Производную находим по формуле 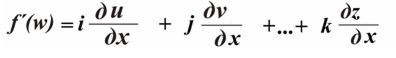
f´(w) = 8x + 2i + 3j
Забегая вперёд, можно сказать, что интеграл, то есть нахождение первообразной функции, взятый по полярностям, будет соответствовать исходной f(w).
В приведённом примере полярности определены. В дальнейшем станет понятным, что при произвольном отношении с полярностями будет полный хаос при интегрировании одних же функций, но в разных полярностях. Поэтому функции должно обозначать согласно полярностям. Например, для переменной x назначим полярность +, для y полярность i и так далее.
Может получиться так, что в одной поляризованной области окажутся две или несколько переменных величин. Например, f(w) = 3ix2 + 5iy3 + ig.
Будет вполне понятным, что речь идёт о полярной области i. Функции переменных величин обозначены по-разному, но каждая из них поляризована одинаково.
Производная f´(w) = 6ix + 15iy + i.
Взяв интеграл от каждой переменной, мы получим исходную функцию. Может показаться, что под вопросом остаётся «безликое» i. Здесь проблем нет: всё, что касалось x и y то они уже определились. Остаётся любая иная переменная, как бы мы её не обозначили.
Обычно, при взятии интеграла, пишут ещё некоторое число, которое могло быть при взятии производной. Если и была какая-то функция или число, то они относятся только к своей полярной области и всегда будут проявлены.
|
|
«Безликой» может оказаться и некоторе число. Например, если взять производную от функции по полярностям f(w) = 5x +7iy +kz, имеющей неполяризованную часть, по формуле
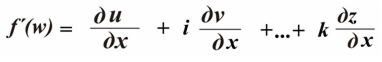 ,
,
то получим f´(w) = 5 + 7i +k.
Ничего неопределённого и искажений такой случай не внесёт, так как интеграл будет взят по каждй части функции, то есть для каждой полярности берётся свой интеграл.
Путаница начинается, когда в одной полярной плоскости находится произведение двух переменных. Например, f(w) = 3ix2y. Производная fx´(w) = 6ixy. Если брать интеграл по dx, то исходная функция получится. Однако нам не известна переменная, поэтому, если взять интеграл по dy, то исходная функция не получается.
Именно поэтому в полярностях функций необходимо определиться чётко.
Эта проблема, то есть соответствия исходной функции и первообразной после взятия интеграла, переносится в раздел Многополярные интегралы.
Интеграл от поляризованных переменных
Интегрирование
Осмысление
Если интегрирование есть сумма бесконечно малых величин, то это не относится к полярностям. Полярность есть дискретное качество по свойствам ума. Полярность может быть результатом взаимодействий некоторой совокупности полярностей, которые есть так же дискретные качества. Однако в ходе операции с поляризованным объектом полярность может совершить переход в иную полярность вместе с объектом, который она окрашивает. Примером тому можно взять функцию z2. Если f(z2) = (ix +jy)2, то f´(z2) = 2z =2(ix +jy).
Здесь функция «свёрнута» и переменные не меняют полярности. Но развернём функцию
f(z) = i2 x2 + 2ijxy + j2y2
Появилась функция, в котором обе переменные поменяли полярность, так как i2, j2, ij отличаются от исходных полярностей.
Именно это внесёт некооректность при нахождении первообразной.
Напомню, что интегрирование, как нахождение некоторой «первообразной», имеет смысл при установлении производной и вновь возвращении к исходной функции.
Следует внести важное замечание: мы имеем дело с функциями, поэтому приписывать к первообразной некоторую постоянную величину нет смысла. Например, при взятии производной есть свойство, что производная от постоянной величины не имеет результата. Итак, речь шла о переменных величинах, то есть о функциях, и упоменание непеременных велечин неуместно, так как можно тогда упоменать о наличии звёзд на небе, деревьев и прочего так же не относящегося к функции. К сожалению математики, по недомыслию, упоминают о «звёздах» и «деревьях». Почему? Причиной тому является синтез ума с анализатором зрения. Появляется представление о графических образах, функции в которых могут быть смещены на некоторую величину в системе координат. Систему координат необходимо предоставлять для функции, если речь идёт о функциональном образе. Другое дело, когда совершается по желанию следующая операция – смещение функции в желаемое место пространства.
|
|
Для чего нужна эта поправка на разумность? Приклеивание к функции того, что к ней отношения не имеет, привело не только к нагромождениям в дифференциальном и интгральном исчислении, но и к абсурду при взятии интегралов, когда первообразные от одного интеграла различные и не совпадают.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!