Вывод уравнений регрессии и геометрическая интерпретация коэффициента корреляции

Уравнение прямой линейной регрессии представляет собой уравнение прямой:

𝑦 = 𝑎 + 𝑏𝑥 (3.6)

Для нахождения коэффициентов в этом уравнении используется метод наименьших квадратов (МНК), т.к. он даёт наименьшую ошибку:

∑^𝑁  [𝑦_𝑖 − (𝑎 + 𝑏𝑥_𝑖)]² → 𝑚𝑖𝑛     (3.7)

𝑖=1

^𝜕 (∑^𝑁

 

[𝑦_𝑖 − (𝑎 + 𝑏𝑥_𝑖)]²) = 0

�𝜕𝑎

𝑖=1

(3.8)

^𝜕 (∑^𝑁 [𝑦_𝑖 − (𝑎 + 𝑏𝑥_𝑖)]²) = 0

𝜕𝑏

𝑖=1

−2 ∑^𝑁 [𝑦_𝑖 − 𝑎 − 𝑏𝑥_𝑖] = 0

�      𝑖=0

𝑖=0

−2 ∑^𝑁  [𝑦_𝑖 − 𝑎 − 𝑏𝑥_𝑖] ∙ 𝑥_𝑖 = 0

(3.9)

∑𝑁

𝑦_𝑖 − 𝑎 ∙ 𝑁 − 𝑏 ∙ ∑^𝑁  𝑥_𝑖 = 0

� 𝑁

𝑖=0

𝑖=0

𝑁                                  𝑁         2

(3.10)

∑𝑖=0 𝑦_𝑖 ∙ 𝑥_𝑖 − 𝑎 ∙ ∑𝑖=0 𝑥_𝑖 − 𝑏 ∙ ∑𝑖=0 𝑥_𝑖 = 0

𝑖=0

{             𝑎 =

𝑁

∑

𝑖=0

𝑦𝑖−𝑏∙∑𝑁

𝑖=0

𝑁

𝑥𝑖

= 𝑦� − 𝑏𝑥̅

 

𝑖=0

(3.11)

∑

𝑁

𝑖=0

𝑦_𝑖 ∙ 𝑥_𝑖 − (𝑦� − 𝑏𝑥̅) ∙ ∑

𝑥_𝑖 − 𝑏 ∙ ∑^𝑁

𝑥_𝑖² = 0

Преобразуем далее второе уравнение системы (3.11):

𝑖=0

𝑏 ∙ (∑^𝑁

𝑥_𝑖² − 𝑥̅ ∙ ∑^𝑁

𝑥_𝑖) = ∑^𝑁

𝑦_𝑖 ∙ 𝑥_𝑖 − 𝑦� ∙ ∑

𝑥_𝑖

(3.12)

𝑖=0

𝑖=0

𝑖=0

𝑖=0

𝑏 ∙ (∑^𝑁  𝑥_𝑖² − 𝑥̅ ∙ 𝑁 ∙ 𝑥̅) = 𝑁 ∙ 𝑥� 𝑦� − 𝑦� ∙ 𝑁 ∙ 𝑥̅    (3.13)

𝑏 ∙ 𝑁 ∙ (�𝑥�2� − 𝑥̅²) = 𝑁 ∙ (�𝑥�𝑦� − 𝑦� ∙ 𝑥̅) (3.14)

𝑏 =

�𝑥�𝑦�−𝑦�∙𝑥

𝑥��2�−𝑥̅2

(3.15)

Коэффициенты уравнения прямой линейной регрессии:

𝑏 = �𝑥�𝑦�−𝑦�∙𝑥̅

�     �𝑥�2�−𝑥̅2

𝑎 = 𝑦� − 𝑏𝑥̅

(3.16)

Уравнение прямой регрессии принимает вид:

𝑦 = 𝑦� + 𝑏(𝑥 − 𝑥̅) (3.17)

Произведем промежуточные вычисления, необходимые для нахождения численного значения коэффициентов, пользуясь исходными данными из таблицы 3.1. Результаты промежуточных вычислений представлены в таблице 3.4.

 

Таблица 3.5. Данные для нахождения коэффициентов регрессии.

 

№	1	2	3	4	Среднее
x	20	40	60	80	50
y	0,405	0,708	0,807	0,945	0,716
x*y	8,1	28,32	48,42	75,6	40,1
𝒙𝟐	400	1600	3600	6400	3000
𝒚𝟐	0,164025	0,501264	0,651249	0,893025	0,552

2

𝑏 = ^{40,1−0,716∙50} = 0,00859 (3.18)

3000−50

𝑎 = 0,716 − 0,00859 ∙ 50 = 0,2865    (3.19)

Окончательно уравнение прямой линейной регрессии:

ℎ(𝑁) = 0,716 + 0,00859 ∙ (𝑁 − 50)    (3.20)

ℎ(𝑁) = 0,00859 ∙ 𝑁 + 0,2865   (3.21)

Уравнение обратной линейной регрессии имеет вид:

𝑥 = 𝑐 + 𝑑𝑦 (3.22)

Вывод аналогичен приведенному для уравнения прямой линейной регрессии, x и y в формулах меняются местами. Получаем:

𝑑 =

�𝑥�𝑦�−𝑦�∙𝑥̅

�     𝑦� �2�−𝑦�2

𝑐 = 𝑥̅ − 𝑑𝑦�

 

(3.23)

𝑥 = 𝑥̅ + 𝑑(𝑦 − 𝑦�) (3.24)

2

𝑑 = ^{40,1−0,716∙50} = 109,138 (3.25)

0,552−0,716

𝑐 = 50 − 109,138 ∙ 0,716 = −28,17    (3.26)

Окончательно уравнение обратной линейной регрессии:

𝑁(ℎ) = 50 + 109,138 ∙ (ℎ − 0,716)  (3.27)

𝑁(ℎ) = 109,138 ∙ ℎ − 28,17 (3.28)

Углы наклона прямых:

 

𝛼_𝑦 = 𝑎𝑟𝑐𝑡𝑔 𝑏 = 𝑎𝑟𝑐𝑡𝑔(0,00859) = 0,492°  (3.29)

𝛼_𝑥 = 𝑎𝑟𝑐𝑡𝑔 𝑑 = 𝑎𝑟𝑐𝑡𝑔(109,138) = 89,475°  (3.30)

𝛽 = 90° − �𝛼_𝑥 + 𝛼_𝑦� = 0,033°            (3.31)

Коэффициент парной корреляции:

𝑟̂ = √𝑏 ∙ 𝑑 = 0,968

Следует проверить, сильно ли отличается от нуля коэффициент корреляции. Выдвигается гипотеза: связи между h и T нет. Для проверки гипотезы надо воспользоваться критерием независимости признаков:

𝑇 = 𝑟 ⋅ √𝑛 − 2 = 0,968 ⋅ √65 − 2 = 30,6

√1 − 𝑟²    �1 − 0, 9682

 

Критерий Стьюдента по приложению 3 для степени свободы n-2 = 63 и уровня значимости α = 0,05:

𝑡_табл = 1,6706 < 30,6

Полученное значение больше табличного, гипотеза отвергается. Коэффициент корреляции значительно отличается от нуля, между h и N существует взаимосвязь.

Рис. 3.7. Экспериментальные точки и линии прямой и обратной регрессии.

Проверка данных по среднему и дисперсии с применением критериев Стьюдента и Фишера

По заданию (Табл. 1.1) требуется проверить гипотезу о принадлежности к одной генеральной совокупности средних значений и дисперсий выборок для 20 и 40 обработанных отверстий. Выборки взяты из Табл. 1.3 и сведены в отдельную таблицу:

Таблица 3.6: Выборки значений h (мм) для заданных значений N, со средними значениями и дисперсиями.

 

№	N, шт.		№	N, шт.
	20	40		20	40
1	0,3	1,3	13	0,2	0,25
2	0,3	0,5	14	0,6	1
3	0,7	0,6	15	0,35	0,8
4	0,2	0,8	16	0,2	0,8
5	0	0,7	17	0	0,9
6	1	1	18	0,3	0,4
7	0,5	0,9	19	0,15	0,2
8	0,5	0,7	20	0,2	0,4
9	0,2	0,6	21	0,3	0,9
10	0,8	0	22	0,1	0,5
11	0,4	0,9	ℎ�, мм.	0,368	0,643
12	0,8	0	𝑆2, мм2	0,069	0,108

 

Проверка по средним значениям

Проведем проверку гипотезы о принадлежности средних значений двух выборок к одной генеральной совокупности с применением критерия Стьюдента. Для проверки по данному критерию воспользуемся формулой:

𝑡 =       |𝑥�� 𝑎 � − 𝑥 � � 𝑏 � |    ∙ � 𝑛 𝑎 𝑛 𝑏 (𝑛 𝑎 + 𝑛 𝑏 − 2),              (3.32)

�𝑛𝑎𝑆2−𝑛𝑏𝑆2

𝑛𝑎+𝑛𝑏

𝑎         𝑏

 

где 𝑥�_𝑎�, 𝑥� _𝑏� - средние значения выборок,

𝑛_𝑎, 𝑛_𝑏 - объемы выборок,

∑𝑛𝑎  (𝑥𝑎𝑖  − 𝑥̅𝑎)2                      ∑𝑛𝑏  (𝑥𝑏𝑖  − 𝑥̅𝑏)2

𝑆2 = 𝑖=1                          , 𝑆2 = 𝑖=1                           ,

𝑎

𝑥_𝑎𝑖, 𝑥_𝑏𝑖 − i-тые элементы выборок.

𝑛_𝑎 − 1          𝑏

𝑛_𝑏 − 1

 

𝑡 = |0,643−0,368|

√22∙0,108−22∙0,069

∙ �22∙22∙(22+22−2) = 6,381           (3.33)

22+22

Данное значение сравниваем с табличным (Приложение 3). Для числа степеней свободы

𝑓 = 𝑛_𝑎 + 𝑛_𝑏 − 2 = 22 + 22 − 2 = 42 и уровня значимости 𝛼 = 0,05; 𝑡_табл = 2,018.

𝑡 > 𝑡_табл - гипотеза отвергается, средние значения двух выборок не относятся к одной генеральной совокупности.

 

Проверка дисперсий

Проведем проверку гипотезы о принадлежности дисперсий двух выборок к одной генеральной совокупности с применением критерия Фишера.

Критерий Фишера:

 

 

Где 𝑆² > 𝑆².

2

𝑆2

𝑆

𝐹 = ²,         (3.34)

1

2           1

𝐹 = ^0,108 = 1,565      (3.35)

0,069

Сравниваем данное значение с табличным (Приложение 4). Для чисел степеней свободы

𝑓₁ = 𝑛₁ − 1 = 22 − 1 = 21; 𝑓₂ = 𝑛₂ − 1 = 22 − 1 = 21 и уровня значимости 𝛼 = 0,05, 𝐹_табл = 2,05.

𝐹 < 𝐹_табл - гипотеза принимается, дисперсии двух выборок относятся к одной генеральной совокупности.

Выводы

o Анализ выборки N показал отсутствие грубых ошибок при проведении эксперимента, это означает, что условия проведения эксперимента нарушены не были, оператор не допустил ошибок, однако данная выборка не подчиняется нормальному закону распределения, согласно проверке по критерию САО, проверке по размаху, проверке с помощью ЭВМ в ПО «NORM».

o Расчет по корреляционной таблице для N и h показал, что между этими двумя параметрами существует положительная корреляция: большим значениям N соответствуют большие значения h.

o В результате аппроксимации данных графическим способом и на ЭВМ было установлено, что с наибольшим по модулю коэффициентом корреляции R=-0,9956, зависимость h(N) аппроксимирует степенная функция ℎ = 1,940335 − 3,76897 ∗ 𝑏 ∙ 𝑁^−0,3.

o Вывод уравнений линейной регрессии показал, что углы наклона линий прямой и обратной регрессии отличаются незначительно, найденный по ним коэффициент корреляции так же близок к единице и равен 𝑟̂ = 0,968. Это говорит о том, что экспериментальная зависимость близка к линейной.

o В результате проверки средних значений выборок h для двух разных чисел отверстий установлено, что они не относятся к одной генеральной совокупности. Это значит, что износ инструмента неодинаков для разного количества обработанных отверстий. Проверка дисперсий для этих двух выборок показала, что они относятся к одной генеральной совокупности. Это значит, что измерения износа были выполнены с одинаковой точностью для этих двух выборок.

Приложения

Приложение 1

Табл. 5.1. Квантили распределения максимального относительного отклонения 𝑟_1−𝑃.

 

n	Уровень значимости α				n	Уровень значимости α
	0,1	0,05	0,025	0,01		0,1	0,05	0,025	0,01
4	1,65	1,69	1,71	1,72	15	2,33	2,49	2,64	2,8
5	1,79	1,87	1,92	1,96	16	2,35	2,52	2,67	2,84
6	1,89	2	2,07	2,13	17	2,38	2,55	2,7	2,87
7	1,97	2,09	2,18	2,27	18	2,4	2,58	2,73	2,9
8	2,04	2,17	2,27	2,37	19	2,43	2,6	2,75	2,93
9	2,1	2,24	2,35	2,46	20	2,45	2,62	2,78	2,96
10	2,15	2,29	2,41	2,54	21	2,47	2,64	2,8	2,98
11	2,19	2,34	2,47	2,61	22	2,49	2,66	2,82	3,01
12	2,23	2,39	2,52	2,66	23	2,5	2,68	2,84	3,03
13	2,26	2,43	2,56	2,71	24	2,52	2,7	2,86	3,05
14	2,3	2,46	2,6	2,76	25	2,54	2,72	2,88	3,07

 

Приложение 2

Табл. 5.2. Критические границы отношения R/S

 

n	Нижние границы		Верхние границы
	а=0,05	а=0,10	а=0,10	а=0,05
8	2,5	2,59	3,308	3,399
10	2,67	2,76	3,57	3,685
12	2,8	2,9	3,78	3,91
14	2,92	3,02	3,95	4,09
16	3,01	3,12	4,09	4,24
18	3,1	3,21	4,21	4,37
20	3,18	3,29	4,32	4,49
25	3,34	3,45	4,53	4,71
30	3,47	3,59	4,7	4,89
35	3,58	3,7	4,84	5,04
40	3,67	3,79	4,96	5,16
45	3,75	3,88	5,06	5,26
50	3,83	3,95	5,14	5,35

Приложение 3

Табл. 5.3. Критические значения коэффициента Стьюдента (t-критерия)

для некоторых значений доверительной вероятности P и числа степеней свободы v.

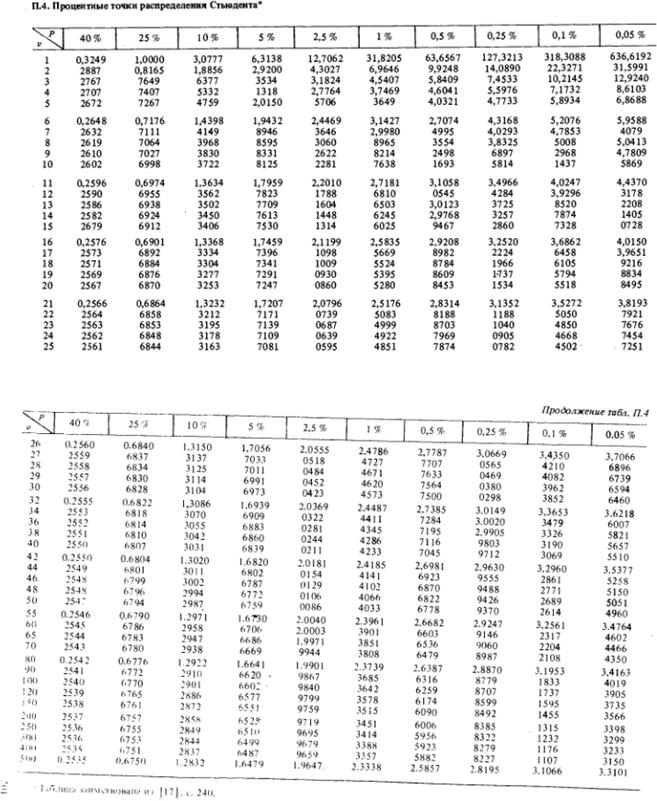Приложение 4

Табл. 5.4. Значения критерия Фишера (F-критерия) для уровня значимости 𝛼 = 0,05.

𝛼 = 0,05		𝑓1
		1	2	3	4	5	6	8	12	24
𝑓2	1	161,45	199,5	215,72	224,57	230,17	233,97	238,89	243,91	249,04
	2	18,51	19	19,16	19,25	19,3	19,33	19,37	19,41	19,45
	3	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64
	4	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77
	5	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53
	6	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4	3,84
	7	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41
	8	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12
	9	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,9
	10	4,96	4,1	3,71	3,48	3,33	3,22	3,07	2,91	2,74
	11	4,84	3,98	3,59	3,36	3,2	3,09	2,95	2,79	2,61
	12	4,75	3,88	3,49	3,26	3,11	3	2,85	2,69	2,5
	13	4,67	3,8	3,41	3,18	3,02	2,92	2,77	2,6	2,42
	14	4,6	3,74	3,34	3,11	2,96	2,85	2,7	2,53	2,35
	15	4,54	3,68	3,29	3,06	2,9	2,79	2,64	2,48	2,29
	16	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,24
	17	4,45	3,59	3,2	2,96	2,81	2,7	2,55	2,38	2,19
	18	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15
	19	4,38	3,52	3,13	2,9	2,74	2,63	2,48	2,31	2,11
	20	4,35	3,49	3,1	2,87	2,71	2,6	2,45	2,28	2,08
	21	4,32	3,47	3,07	2,84	2,68	2,57	2,42	2,25	2,05
	22	4,3	3,44	3,05	2,82	2,66	2,55	2,4	2,23	2,03
	23	4,28	3,42	3,03	2,8	2,64	2,53	2,38	2,2	2
	24	4,26	3,4	3,01	2,78	2,62	2,51	2,36	2,18	1,98