| Любое множество A детерминировано.
|
Аксиома детерминированности — аксиома теории множеств, её предложили в 1962 году польские математики Ян Мычельский и Гуго Штейнгауз в качестве замены для аксиомы выбора.
Причиной поиска альтернативы аксиоме выбора стали необычные следствия из этой аксиомы, которые вызывали и продолжают вызывать критику со стороны части математиков. Многие следствия конкурирующих аксиом противоположны друг другу. С помощью аксиомы выбора доказано, что существуют множества вещественных чисел, неизмеримые по Лебегу; из аксиомы детерминированности следует, что таких множеств не существует — все множества вещественных чисел измеримы.
По-разному решается проблема континуума (существование промежуточных мощностей между счётной и континуальной). Аксиоматика Цермело—Френкеля допускает любой из двух вариантов решения этой проблемы (то есть, она не может быть ни доказана, ни опровергнута), недоказуемость этой гипотезы в рамках аксиоматики ZFC показана Коэном в 1963 г. В то время как из аксиомы детерминированности выводится однозначное решение: любое бесконечное несчётное множество вещественных чисел континуально.
Аксиомы теории множеств.
Система аксиом ZFC (Цермело-Френкеля с аксиомой выбора).
0. Аксиома пустого множества  .
.
1. Условие равенства множеств (аксиома объёмности).
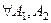 верно, что если
верно, что если 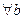 :
:  то
то 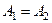 .
.
2. Существование множества из двух элементов (аксиома пары).
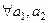
 , такое что
, такое что 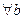 :
: 
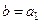 или
или  .
.
3. Аксиома объединения. Из любого семейства 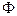 множеств
множеств  можно образовать как минимум одно такое множество
можно образовать как минимум одно такое множество 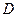 , каждый элемент
, каждый элемент  которого принадлежит хотя бы одному множеству
которого принадлежит хотя бы одному множеству  данного семейства
данного семейства 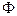 .
.
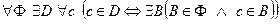 .
.
4. Аксиома пересечения. Из любого семейства 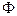 множеств
множеств  можно образовать как минимум одно такое множество
можно образовать как минимум одно такое множество 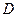 , каждый элемент
, каждый элемент  которого принадлежит всем множествам данного семейства
которого принадлежит всем множествам данного семейства 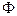 .
.
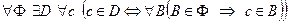 .
.
5. Существование подмножества, элементы которого удовлетворяют некоторому свойству.
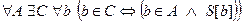 .
.
6. Существование бесконечного множества.
 = {Ø, {Ø}, {Ø,{Ø},... }
= {Ø, {Ø}, {Ø,{Ø},... }
7. Существование образа функции
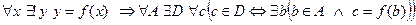
т.е. если кратко, то  .
.
8. Аксиома регулярности. Любое непустое семейство множеств 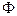 содержит множество
содержит множество  , все элементы которого не принадлежат семейству
, все элементы которого не принадлежат семейству 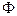 .
.
9. Аксиома выбора. Для любого класса не пересекающихся непустых множеств существует множество, содержащее только по одному элементу из каждого множества.
Прим – бесконечное мн-во прямых на пл-ти (континуум). Не сущ пр, пересекающ со всеми только в 1 точке.
10. Аксиома степени (аксиома булеана). Можно образовать 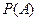 множество всех подмножеств данного множества.
множество всех подмножеств данного множества.
Упорядоченные множества.
Говорят, что на множестве М задано бинарное отношение R, если задано подмножество декартового произведения:  .
.
Примеры. Отношения на множестве 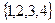
Отношение равенства: 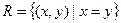
Можно перечислить все пары элементов, находящихся в данном отношении: 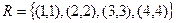 .
.



 .
. 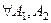 верно, что если
верно, что если 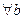 :
:  то
то 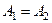 .
. 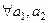
 , такое что
, такое что 
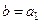 или
или  .
. 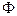 множеств
множеств  можно образовать как минимум одно такое множество
можно образовать как минимум одно такое множество 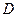 , каждый элемент
, каждый элемент  которого принадлежит хотя бы одному множеству
которого принадлежит хотя бы одному множеству 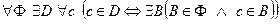 .
. 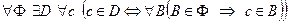 .
. 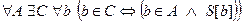 .
.  = {Ø, {Ø}, {Ø,{Ø},... }
= {Ø, {Ø}, {Ø,{Ø},... } 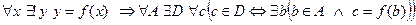
 .
. 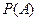 множество всех подмножеств данного множества.
множество всех подмножеств данного множества. .
.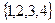
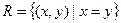
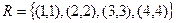 .
.

