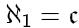.
.
Доказательство. Можно по индукции, но это дольше, более кратко с помощью характеристических функций.
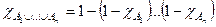 =
=
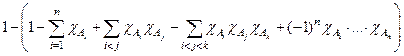 =
=

Бесконечное множество.
С бесконечными множествами связаны различные парадоксы. Например, если переставить бесконечное число слагаемых, сумма может измениться.
Пример. Вспомним разложение функции по формуле Тейлора:
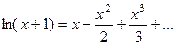
при  получается
получается 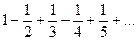 = ln2.
= ln2.
Переставим так, чтобы после каждого положительного члена ряда следовали ровно по 2 отрицательных.
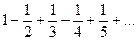 =
= 
объединим первые 2 слагаемых в каждой скобке.
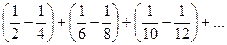 а теперь вынесем
а теперь вынесем  .
.
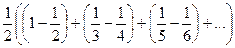 =
= 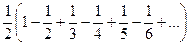 мы получили точно такой же ряд, как и был в начале, но с коэффициентом
мы получили точно такой же ряд, как и был в начале, но с коэффициентом  . То есть сумма теперь должна быть не ln2, а
. То есть сумма теперь должна быть не ln2, а  .
.
Множество целых чисел 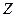 , рациональных
, рациональных  и действительных чисел
и действительных чисел  являются бесконечными, но на каждом полуинтервале длины 1 бесконечное множество действительных и рациональных чисел, и всего лишь одна точка из
являются бесконечными, но на каждом полуинтервале длины 1 бесконечное множество действительных и рациональных чисел, и всего лишь одна точка из 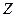 . Надо обобщить понятие мощности с конечного множества на бесконечное, и научиться сравнивать мощности бесконечных множеств.
. Надо обобщить понятие мощности с конечного множества на бесконечное, и научиться сравнивать мощности бесконечных множеств.
Множества называются равномощными, если между ними можно установить взаимно однозначное соответствие, при котором каждому элементу одного множества соответствует ровно один элемент другого.
Например, можем рассматривать биективную функцию, отображающую множество  в его часть
в его часть  ,
,  . Бесконечное множество равномощно своему собственному подмножеству (для конечных такого быть не могло).
. Бесконечное множество равномощно своему собственному подмножеству (для конечных такого быть не могло).
Счётным множеством называется множество, равномощное множеству натуральных чисел  .
.
Множество целых чисел 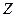 равномощно
равномощно  , несмотря на то, что содержит в 2 раза больше чисел. Можно пронумеровать все целые числа с помощью натуральных, расположив их так:
, несмотря на то, что содержит в 2 раза больше чисел. Можно пронумеровать все целые числа с помощью натуральных, расположив их так:
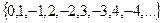
Мощность счётного множества обозначается ﬡ0 (алеф-ноль)
(в этой теории используются не латинские и даже не греческие буквы, а из иврита). ﬡ1 - наименьшая мощность несчётного множества (первый несчётный кардинал).
Кардиналы, или кардинальные числа ﬡ0, ﬡ1,...
Если добавить n элементов к счётному множеству, оно снова будет счётным. Действительно, можно пронумеровать сначала эти n элементов, а затем то множество, которые было до того (начиная с номера  ). В обозначениях мощностей: ﬡ0 + n = ﬡ0 .
). В обозначениях мощностей: ﬡ0 + n = ﬡ0 .
Кардинальные числа ﬡ0, ﬡ1,... (соотв.  , мат.ан:
, мат.ан:  ).
).
Мощность множества действительных чисел называется континнум, обозначается  .
.
Если кардинал  бесконечен, то:
бесконечен, то:
1)  , 2)
, 2)  .
.
Принцип математической индукции. Допустим, что утверждение P(1) верно (называется базой индукции.) Для любого n доказано, что если верно P(n), то верно P(n+1) (это утверждение называется индукционным переходом.) Тогда все утверждения верны для любого  .
.
Доказать можно «от противного». Пусть  - наименьшее натуральное число, для которого утверждение неверно.
- наименьшее натуральное число, для которого утверждение неверно.
1) Если 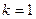 , сразу противоречие, т.к. P(1) верно.
, сразу противоречие, т.к. P(1) верно.
2) Если 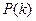 неверно, и
неверно, и  - наименьшее натуральное число с таким свойством. Тогда
- наименьшее натуральное число с таким свойством. Тогда  верно. Но из верности
верно. Но из верности  следовало бы, что
следовало бы, что 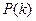 верно. □
верно. □
Ранее доказали, что множество целых чисел 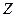 равномощно
равномощно  , т.е. объединение двух счётных множеств счётно:
, т.е. объединение двух счётных множеств счётно:  , т.е. есть
, т.е. есть  . Аналогично,
. Аналогично,  для любого
для любого 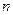 .
.
Док-во. Можно доказать это с помощью принципа математической индукции. Пусть для  указанное верно, то есть объединение
указанное верно, то есть объединение  счётных множеств счётно. Добавим ещё одно счётное множество.
счётных множеств счётно. Добавим ещё одно счётное множество.
Обозначим  - элементы ранее полученного счётного множества,
- элементы ранее полученного счётного множества,  - элементы добавляемого множества.
- элементы добавляемого множества.
Можем образовать последовательность  таким образом, новое множество тоже счётно, и
таким образом, новое множество тоже счётно, и  .
.
Лемма.
1) Подмножество счётного множества конечно или счётно.
2) Всякое бесконечное множество содержит счётное подмножество.
Доказательство.
1) Представим множество  в виде:
в виде:  Выбросим те члены последовательности, которые не принадлежат
Выбросим те члены последовательности, которые не принадлежат  . Оставшиеся элементы образуют либо бесконечную подпоследовательность, либо конечную.
. Оставшиеся элементы образуют либо бесконечную подпоследовательность, либо конечную.
2) Если множество  бесконечно, то можно выбрать последовательность
бесконечно, то можно выбрать последовательность 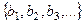 , после выбора каждого
, после выбора каждого 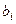 остаётся ещё бесконечное множество неиспользованных элементов, потому что множество бесконечное.
остаётся ещё бесконечное множество неиспользованных элементов, потому что множество бесконечное.
Теорема. Если  бесконечное множество,
бесконечное множество,  конечное или счётное, то
конечное или счётное, то 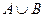 равномощно
равномощно  .
.
Доказательство. Если 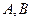 пересекаются, выбросим пересечение из
пересекаются, выбросим пересечение из  , получив новое множество
, получив новое множество  , которое снова будет конечным либо счётным. Далее считаем, что они не пересекаются.
, которое снова будет конечным либо счётным. Далее считаем, что они не пересекаются.
Выделим в  счётное подмножество
счётное подмножество 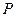 , остаток обозначим
, остаток обозначим 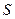 .
.
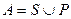 .
.  .
.
 и
и  оба счётны, между ними существует взаимно однозначное соответствие. Каждый элемент из
оба счётны, между ними существует взаимно однозначное соответствие. Каждый элемент из 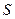 соответствует самому себе. Таким образом, есть взаимно однозначное соответствие между
соответствует самому себе. Таким образом, есть взаимно однозначное соответствие между
 и
и 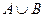 .
.
Теорема. Счётное множество счётных множеств счётно.
Расположим по горизонтали каждое из множеств.
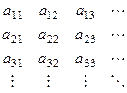
Из элементов этого множества можно образовать такую последовательность: 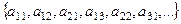
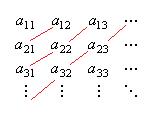
Если исходные множества пересекаются, то часть повторяющихся элементов исключить, получим подпоследовательность, она тоже счётна. При этом она не будет конечна, так как хотя бы одно из исходных множеств счётно.
В обозначениях операций над мощностями, это пишется так:
ﬡ0 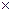 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0
Итак,
1) ﬡ0 + n = ﬡ0
2) ﬡ0 + ﬡ0 = ﬡ0, 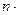 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0
3) ﬡ0 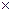 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0
Пусть  - мощность множества А,
- мощность множества А, 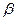 - мощность множества В,
- мощность множества В,
 Ǿ. Тогда
Ǿ. Тогда
Сумма  мощностей - это мощность множества
мощностей - это мощность множества 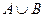 ,
,
Произведение 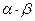 мощностей - это мощность множества
мощностей - это мощность множества  .
.
Для бесконечных мощностей, 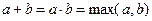 .
.
Примеры.
Множество рациональных чисел  равномощно
равномощно  .
.
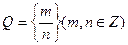 . Декартово произведение
. Декартово произведение 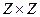 равномощно
равномощно  , можно пронумеровать:
, можно пронумеровать:


В каждом из слоёв конечное количество элементов. Начиная от внутренних прямоугольников, можно пронумеровать все элементы с помощью натуральных чисел.
ЛЕКЦИЯ 2. 13.2.2021
Теорема (Кантора). Множество всех подмножеств счётного множества не является счётным.
Доказательство. Допустим, что искомое множество счётно. Тогда все подмножества можно расположить по порядку, представив то или иное подмножество в каждой строке с помощью 0 и 1 (1 если элемент принадлежит подмножеству, 0 если нет).
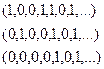
…
Рассмотрим диагональ:

Построим такое подмножество: изменим 0 на 1 и 1 на 0 на всех местах. Напр, здесь было бы 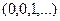 . Оно не совпадает ни с одним из подмножеств, представленных в этой последовательности: с первым не совпадает на 1-м элементе, со вторым на 2-м и так далее.
. Оно не совпадает ни с одним из подмножеств, представленных в этой последовательности: с первым не совпадает на 1-м элементе, со вторым на 2-м и так далее.
Итак, множество всех подмножеств счётного множества не является счётным.
Аналогично, докажем, что (0,1) не является счётным множеством.
Теорема. Интервал (0,1) не является счётным множеством.
Доказательство. Пусть все действительные числа, составляющие (0,1), образуют счётное множество. Каждое из них представим в виде десятичной дроби, 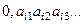 Расположим по порядку эти числа, если множество счётное:
Расположим по порядку эти числа, если множество счётное:
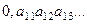
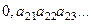
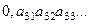
....
Можно рассмотреть такое число:  , взяв значения десятичных разрядов по диагонали.
, взяв значения десятичных разрядов по диагонали.
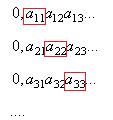
Если теперь в  изменить каждую цифру на какую-либо другую, то получим новое число, которое не совпадает ни с одним из имеющихся в этом множестве. Таким образом, множество не счётное.
изменить каждую цифру на какую-либо другую, то получим новое число, которое не совпадает ни с одним из имеющихся в этом множестве. Таким образом, множество не счётное.
Теорема Кантора-Бернштейна.
Если множество  равномощно подмножеству множества
равномощно подмножеству множества  , а
, а  равномощно подмножеству множества
равномощно подмножеству множества  , то
, то  и
и  равномощны.
равномощны.
Доказательство.
Пусть множество  равномощно некоторому
равномощно некоторому  - подмножеству множества
- подмножеству множества  . Т.е. существует некоторая функция
. Т.е. существует некоторая функция  , которая инъективна, но не сюръективна. При этом
, которая инъективна, но не сюръективна. При этом 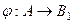 биекция.
биекция.
Аналогично  равномощно некоторому подмножеству
равномощно некоторому подмножеству 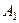 множества
множества  , и существует инъективная функция
, и существует инъективная функция  , при этом
, при этом 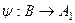 биекция.
биекция.
Тогда для композиции 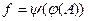 есть некоторое множество
есть некоторое множество 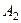 - «образ образа» множества
- «образ образа» множества  . При этом
. При этом 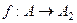 - биекция.
- биекция.
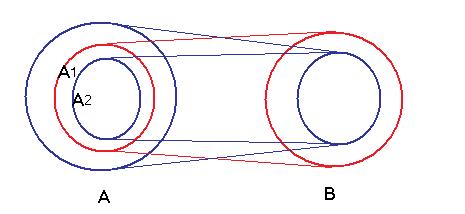
Так как 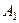 равномощно
равномощно  , то нужно фактически доказать, что равномощны
, то нужно фактически доказать, что равномощны  и
и 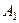 , то есть построить биективное отображение.
, то есть построить биективное отображение.
При этом  равномощны.
равномощны.
Применяя функции  и
и  несколько раз, получим последовательность множеств:
несколько раз, получим последовательность множеств: 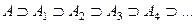 при этом
при этом 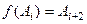 . Пересечение
. Пересечение 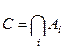 возможно, непустое множество.
возможно, непустое множество.
Обозначим  ,
, 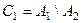 ,... При этом
,... При этом 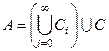 .
.
Биективное отображение 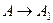 можно построить следующим образом.
можно построить следующим образом.  для нечётных
для нечётных  и для
и для  ,
, 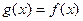 для чётных
для чётных  . При этом
. При этом 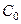 перейдёт в
перейдёт в 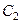 ,
, 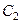 в
в 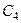 и так далее.
и так далее.
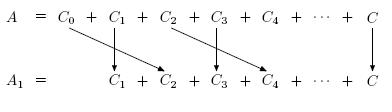
А равномощно А1, А1 равномощно В.
Континуум-гипотеза (проблема континуума) — выдвинутое в 1877 году Георгом Кантором предположение о том, что любое бесконечное подмножество континуума является либо счётным, либо континуальным. Другими словами, гипотеза предполагает, что мощность континуума — наименьшая, превосходящая мощность счётного множества.
Континуум-гипотеза (первый несчётный кардинал имеет мощность континуума):
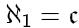
Аксиома выбора
| Для всякого семейства X непустых множеств существует функция f, которая каждому множеству семейства сопоставляет один из элементов этого множества.
|
Аксиома выбора была сформулирована и опубликована Эрнстом Цермело в 1904 году. Новая аксиома вызвала бурную полемику и до сих пор не все математики принимают её безоговорочно.




 .
. =
=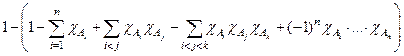 =
=
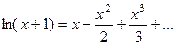
 получается
получается 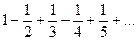 = ln2.
= ln2. 
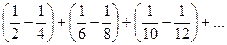 а теперь вынесем
а теперь вынесем  .
.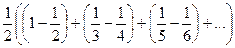 =
= 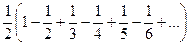 мы получили точно такой же ряд, как и был в начале, но с коэффициентом
мы получили точно такой же ряд, как и был в начале, но с коэффициентом  .
. 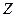 , рациональных
, рациональных  и действительных чисел
и действительных чисел  являются бесконечными, но на каждом полуинтервале длины 1 бесконечное множество действительных и рациональных чисел, и всего лишь одна точка из
являются бесконечными, но на каждом полуинтервале длины 1 бесконечное множество действительных и рациональных чисел, и всего лишь одна точка из  в его часть
в его часть  ,
,  . Бесконечное множество равномощно своему собственному подмножеству (для конечных такого быть не могло).
. Бесконечное множество равномощно своему собственному подмножеству (для конечных такого быть не могло).  .
.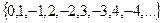
 ). В обозначениях мощностей: ﬡ0 + n = ﬡ0 .
). В обозначениях мощностей: ﬡ0 + n = ﬡ0 . , мат.ан:
, мат.ан:  ).
). .
.  бесконечен, то:
бесконечен, то: , 2)
, 2)  .
.  .
. - наименьшее натуральное число, для которого утверждение неверно.
- наименьшее натуральное число, для которого утверждение неверно.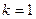 , сразу противоречие, т.к. P(1) верно.
, сразу противоречие, т.к. P(1) верно.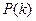 неверно, и
неверно, и  верно. Но из верности
верно. Но из верности  , т.е. есть
, т.е. есть  . Аналогично,
. Аналогично,  для любого
для любого 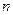 .
. указанное верно, то есть объединение
указанное верно, то есть объединение  - элементы ранее полученного счётного множества,
- элементы ранее полученного счётного множества,  - элементы добавляемого множества.
- элементы добавляемого множества. таким образом, новое множество тоже счётно, и
таким образом, новое множество тоже счётно, и  в виде:
в виде:  Выбросим те члены последовательности, которые не принадлежат
Выбросим те члены последовательности, которые не принадлежат  . Оставшиеся элементы образуют либо бесконечную подпоследовательность, либо конечную.
. Оставшиеся элементы образуют либо бесконечную подпоследовательность, либо конечную.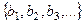 , после выбора каждого
, после выбора каждого 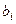 остаётся ещё бесконечное множество неиспользованных элементов, потому что множество бесконечное.
остаётся ещё бесконечное множество неиспользованных элементов, потому что множество бесконечное.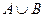 равномощно
равномощно 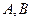 пересекаются, выбросим пересечение из
пересекаются, выбросим пересечение из 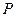 , остаток обозначим
, остаток обозначим 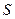 .
. 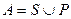 .
.  .
. 
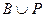 и
и 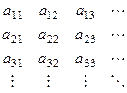
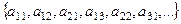

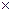 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0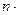 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0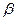 - мощность множества В,
- мощность множества В,  Ǿ. Тогда
Ǿ. Тогда мощностей - это мощность множества
мощностей - это мощность множества 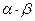 мощностей - это мощность множества
мощностей - это мощность множества  .
. 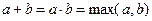 .
.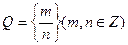 . Декартово произведение
. Декартово произведение 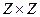 равномощно
равномощно 

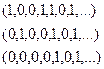

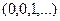 . Оно не совпадает ни с одним из подмножеств, представленных в этой последовательности: с первым не совпадает на 1-м элементе, со вторым на 2-м и так далее.
. Оно не совпадает ни с одним из подмножеств, представленных в этой последовательности: с первым не совпадает на 1-м элементе, со вторым на 2-м и так далее.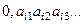 Расположим по порядку эти числа, если множество счётное:
Расположим по порядку эти числа, если множество счётное: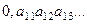
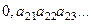
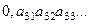
 , взяв значения десятичных разрядов по диагонали.
, взяв значения десятичных разрядов по диагонали.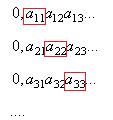
 - подмножеству множества
- подмножеству множества  , которая инъективна, но не сюръективна. При этом
, которая инъективна, но не сюръективна. При этом 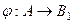 биекция.
биекция.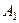 множества
множества  , при этом
, при этом 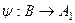 биекция.
биекция.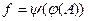 есть некоторое множество
есть некоторое множество 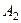 - «образ образа» множества
- «образ образа» множества 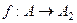 - биекция.
- биекция.
 равномощны.
равномощны.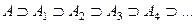 при этом
при этом 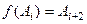 . Пересечение
. Пересечение 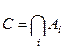 возможно, непустое множество.
возможно, непустое множество.  ,
, 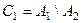 ,... При этом
,... При этом 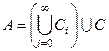 .
. 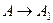 можно построить следующим образом.
можно построить следующим образом.  для нечётных
для нечётных  и для
и для  ,
, 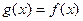 для чётных
для чётных 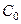 перейдёт в
перейдёт в 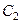 ,
, 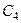 и так далее.
и так далее.