

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Неприводимые представления и характеры циклических точечных групп можно построить непосредственно, руководствуясь следующими правилами:
1. Для групп Cn при четном n существует представление A и B (одномерные) и множество двумерных представлений Ek с k=1,2,..., (n/2)-1.
2. Если n нечетное, то представления B не существует, а индекс k для Ek принимает значения k=1,2,..., (n-1)/2.
Характеры для пар вырожденных представлений Ek равны e(2 p i/n) jk и e(-2 p i/n) jk , где k - индекс Ek, а j определяется элементом симметрии Cn j .
3. Характеры представлении A и B можно получить как особые случаи Ek с k=0 или (n/2), соответственно. Т.о. представление A - полносимметричное с характерами c =1. Поскольку e(2 p i/n) 0 = e0=1. Для B имеем
e(2 p i/n) jn/2 = ej p i = cos(jp) - isin(jp) = cos(jp), т.к. sin(jp)=0 и т.о.
c (B)= cos(jp) = ± 1 (+1 при четных j и -1 при нечетных j).
Например, для группы C3 имеем представления A и E1 или просто E и таблицу характеров.
| С3 | E | C3 | C3 2 |
| A | 1 | 1 | 1 |
E 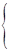
| 
| 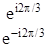
| 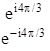
|
e4pi/3= e-2pi/3; e-4pi/3= e2pi/3; т.к. 4p/3=240о=-2p/3=-120о.
Действительное представление получается при использовании формулы Ейлера:
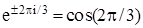 + -
+ - 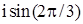 .
.
Таким образом для C3 получим.
| С3 | E | C3 | C3 2 |
| A | 1 | 1 | 1 |
Eкомпл. 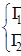
| 
| 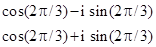
| 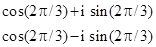
|
| G1+G2 | 2 | 2cos(2p/3) | 2cos(2p/3) |
| Eдействит. | 2 | -1 | -1 |
Рассмотрим группу C6:
В соответствии с правилами 1-3 имеем представления A, B, E1 и E2 и обозначая e2pi/6=e, а комплексносопряженную как e* получим следующую таблицу характеров:
| С6 | E | C6 | C6 2 =C3 | C63 =C2 | C64 =C32 | C65 |
| A | 1 | 1 | 1 | 1 | 1 | 1 |
| B | 1 | -1 | 1 | -1 | 1 | -1 |
E1 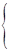
| 
| 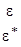
| 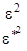
| 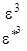
| 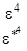
| 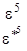
|
E2 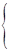
| 
| 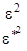
| 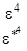
| 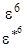
| 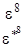
| 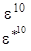
|
Учитывая, что e*=cos(60o)+isin(60o) и
e2=cos(120o)-isin(120o)=-cos(60o)-isin(60o)=-(cos(60o)+isin(60o))=-e* и т.д. таблицу характеров можно записать в виде:
| С6 | E | C6 | C3 | C2 | C3 2 | C65 |
| A | 1 | 1 | 1 | 1 | 1 | 1 |
| B | 1 | -1 | 1 | -1 | 1 | -1 |
E1 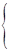
| 
| 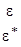
| 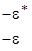
| 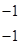
| 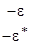
| 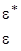
|
E2 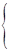
| 
| 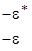
| 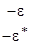
| 
| 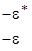
| 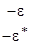
|
В действительном виде таблица характеров запишется как:
|
|
| С6 | E | 2C6 | 2C3 | C2 |
| A | 1 | 1 | 1 | 1 |
| B | 1 | -1 | 1 | -1 |
| E1 | 2 | 1 | -1 | -2 |
| E2 | 2 | -1 | -1 | 2 |
Таблицы характеров остальных подгрупп можно построить из прямого или полупрямого произведения подгрупп. Рассмотрим процедуру построения, например, для группы D2h=D2´Cs. На первом этапе используя операции симметрии подгрупп находим операции симметрии группы и это отобразим в виде таблицы (1)
| D2 | ||||
| Cs | E | C2z | C2y | C2x |
| E | E | C2z | C2y | C2x |
| sxy | sxy | i | syz | sxz |
(1)
Т. о. для группы D2h имеем 8 операций симметрии. Можно, показать, что каждая из них образует отдельный класс.
На втором этапе зная представления подгрупп получим таблицу произведений неприводимых представлений подгрупп (2):
| D2 | ||||
| Cs | A1 | B1 | B2 | B3 |
| A¢ | A¢A1 | A¢B1 | A¢B2 | A¢B3 |
| A² | A²A1 | A²B1 | A²B2 | A²B3 |
(2)
| Cs | E | sxy |
| A¢ | 1 | 1 |
| A² | 1 | -1 |
В таблице (2) получено 8 представлений группы. Число представлений равно числу классов группы. Следовательно все эти представления - неприводимые. Для нахождения характеров неприводимых представлений группы нужно знать таблицы характеров неприводимых представлений подгрупп.
| D2 | E | C2z | C2y | C2x |
| A1 | 1 | 1 | 1 | 1 |
| B1 | 1 | 1 | -1 | -1 |
| B2 | 1 | -1 | 1 | -1 |
| B3 | 1 | -1 | -1 | 1 |
На третьем этапе для каждой пары из табл. 2 найдем произведения характеров соответствующих неприводимых представлений подгрупп и результаты представим в виде 8-ми таблиц похожих по форме на табл. 1.
|
| D2 | D2 | ||||||||||
| Cs | E | C2z | C2y | C2x | Cs | E | C2z | C2y | C2x | |||
|
| A1 | (3) | A1 | (7) | ||||||||
| A¢ | 1 | 1 | 1 | 1 | A² | 1 | 1 | 1 | 1 | |||
| E | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| sxy | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
|
| D2 | D2 | ||||||||||
| Cs | E | C2z | C2y | C2x | Cs | E | C2z | C2y | C2x | |||
|
| B1 | (4) | B1 | (8) | ||||||||
| A¢ | 1 | 1 | -1 | -1 | A² | 1 | 1 | -1 | -1 | |||
| E | 1 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | -1 | ||
| sxy | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | ||
|
| D2 | D2 | |||||||||||
| Cs | E | C2z | C2y | C2x | Cs | E | C2z | C2y | C2x | ||||
|
| B2
| (5) | B2 | (9) | |||||||||
| A¢ | 1 | -1 | 1 | -1 | A² | 1 | -1 | 1 | -1 | ||||
| E | 1 | 1 | -1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | |||
| sxy | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | -1 | 1 | |||
|
| D2 | D2 | ||||||||||
| Cs | E | C2z | C2y | C2x | Cs | E | C2z | C2y | C2x | |||
|
| B3 | (6) | B3 | (10) | ||||||||
| A¢ | 1 | -1 | -1 | 1 | A² | 1 | -1 | -1 | 1 | |||
| E | 1 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | -1 | 1 | ||
| sxy | 1 | 1 | -1 | -1 | 1 | -1 | -1 | 1 | 1 | -1 | ||
Значения характеров в ячейках табл. 3-10 соответствуют элементам симметрии размещенным в аналогичных ячейках табл. 1.
Таблицы 3-10 можно объединить в одну таблицу характеров группы D2h. При этом для обозначения произведений представлений в табл. 2 используются определенные правила, которые будут разобраны нами на следующих занятиях.
Таблица характеров для группы D2h.
| D2h | E | C2z | C2y | C2x | sxy | i | syz | sxz |
| Ag | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| B1g | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 |
| B2u | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
| B3u | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 |
| Au | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
| B1u | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 |
| B2g | 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 |
| B3g | 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
В случае полупрямого произведения процедура построения таблицы характеров несколько усложняется. Рассмотрим группу C3v=C3ÙCs. Найдем операции симметрии группы (табл. 11):
| Cs | ||
| C3 | E | sv |
| E | E | sv |
| C3 | C3 | sv¢ |
| C32 | C32 | sv² |
(11)
Если по вертикали записаны элементы симметрии инвариантной подгруппы, то столбцы будут содержать классы группы. Для группы C3v имеем 3 класса {E, 2C3, 3sv }и, следовательно, должно быть 3 неприводимых представления. Составим таблицу произведения неприводимых представлений подгрупп.
| Cs | |||
| С3 | A¢ | A² | |
| A | AA¢ | AA² | (12) |
E 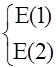
| 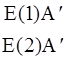
| 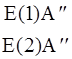
| |
В табл. 12 есть 6 пар произведений, но в группе С3v должно быть только три неприводимых представления. При этом нужно учесть, что произведения полносимметричного представления (А) группы C3v дают всегда неприводимые представления. Т.о. произведения AA¢ и AA² в табл. 12 - два неприводимых представления. Очевидно, 4 оставшихся являются зависимыми.
Получим характеры представлений.
| AA¢ | Сs | AA² | Сs | |||||
| С3 | E | sv | E | sv | ||||
|
| A¢ | A² | ||||||
| A | 1 | 1 | A | 1 | -1 | |||
| E | 1 | 1 | 1 | (13) | 1 | 1 | -1 | (14) |
| С3 | 1 | 1 | 1 | 1 | 1 | -1 | ||
| C32 | 1 | 1 | 1 | 1 | 1 | -1 | ||
| E(1)A¢ | Сs | E(1)A² | Сs | |||||
| С3 | E | sv | E | sv | ||||
|
| A¢ | A² | ||||||
| E(1) | 1 | 1 | E(1) | 1 | -1 | |||
| E | 1 | 1 | 1 | (15) | 1 | 1 | -1 | (16) |
| С3 | e | e | e | e | e | -e | ||
| C32 | e* | e* | e* | e* | e* | -e* | ||
|
|
| E(2)A¢ | Сs | E(2)A² | Сs | |||||
| С3 | E | sv | E | sv | ||||
|
| A¢ | A² | ||||||
| E(2) | 1 | 1 | E(2) | 1 | -1 | |||
| E | 1 | 1 | 1 | (17) | 1 | 1 | -1 | (18) |
| С3 | e* | e* | e* | e* | e* | -e* | ||
| C32 | e | e | e | e | e | -e | ||
Для нахождения третьего представления проведем усреднение характеров элементов по классам для каждого из 4-х зависимых представлений. Получим:
| E | 2C3 | 3sv | E | 2C3 | 3sv | ||
| E(1)A¢ | 1 | (e+e*)/2 | (1+e+e*)/3 | E(1)A² | 1 | (e+e*)/2 | -(1+e+e*)/3 |
| (1 | -1/2 | 0) | (1 | -1/2 | 0) | ||
| E(2)A¢ | 1 | (e*+e)/2 | (1+e*+e)/3 | E(2)A² | 1 | (e*+e)/2 | -(1+e*+e)/3 |
| (1 | -1/2 | 0) | (1 | -1/2 | 0) | ||
| Cумма | 2 | -1 | 0 | Cумма | 2 | -1 | 0 |
Т.о. получены два совершенно одинаковых представления и это будет в группе C3v - третье представление. Таблица характеров будет выглядеть следующим образом:
| C3v | E | 2C3 | 3sv |
| A1 | 1 | 1 | 1 |
| A2 | 1 | 1 | -1 |
| E | 2 | -1 | 0 |
Таблица характеров для группы Td.
Td = D2 ^ C3v
Элементы симметрии группы Td.
| C3v | |||
| D2 | E | 2C3 | 3sv |
| E | E | 2C3 | 3sd |
| C2z | C2z | 2C3¢ | 3sd¢ |
| C2y | C2y | 2C3² | 3S4 |
| C2x | C2x | 2C3²¢ | 3S4¢ |
sv - в тетраэдре соответствует sd.
Т.о. имеется 5 классов Td={E, 3C2, 8C3, 6sd, 6S4}.
Таблица произведений представлений:
| C3v | |||
| D2 | A1 | A2 | E |
| A1 | A1A1 | A1A2 | A1E |
| B1 | B1A1 | B1A2 | B1E |
| B2 | B2A1 | B2A2 | B2E |
| B3 | B3A1 | B3A2 | B3E |
Произведения A1A1, A1A2, A1E образуют три неприводимых представления.
Остальные 9 - зависимые и из нужно получить еще два неприводимых представления. Для нахождения этих представлений построим таблицу произведений характеров соответствующих неприводимых представлений подгрупп.
|
| C3v | |||||||||
|
| A1 | A2 | E | |||||||
| D2 | E | 2C3 | 3sv | E | 2C3 | 3sv | E | 2C3 | 3sv | |
|
| 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 | |
| B1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 | |
| -1 | -1 | -1 | -1 | -1 | -1 | 1 | -2 | 1 | 0 | |
| -1 | -1 | -1 | -1 | -1 | -1 | 1 | -2 | 1 | 0 | |
| B2 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 |
| -1 | -1 | -1 | -1 | -1 | -1 | 1 | -2 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 | |
| -1 | -1 | -1 | -1 | -1 | -1 | 1 | -2 | 1 | 0 | |
| B3 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 |
| -1 | -1 | -1 | -1 | -1 | -1 | 1 | -2 | 1 | 0 | |
| -1 | -1 | -1 | -1 | -1 | -1 | 1 | -2 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | -1 | 2 | -1 | 0 | |
Одинаковым фоном выделены характеры элементов симметрии, относящиеся к одному классу группы Td.
Просуммируем для зависимых представлений характеры по классам элементов симметрии (классы в табл. выделены одним фоном) и усредним. В результате получим:
|
|
| E | 3C2 | 8C3 | 6sd | 6S4 | |
| B1A1 | (1) 1 | (1-1-1)/3 -1/3 | (1+1-1-1)/4 0 | (1+1)/2 1 | (-1-1)/2 -1 |
| B2A1 | 1 | -1/3 | 0 | 0 | 0 |
| B3A1 | 1 | -1/3 | 0 | 0 | 0 |
| S | 3 | -1 | 0 | 1 | -1 |
| B1A2 | 1 | -1/3 | 0 | -1 | 1 |
| B2A2 | 1 | -1/3 | 0 | 0 | 0 |
| B3A2 | 1 | -1/3 | 0 | 0 | 0 |
| S | 3 | -1 | 0 | -1 | 1 |
| B1E | 2 | -2/3 | 0 | 0 | 0 |
| B2E | 2 | -2/3 | 0 | 0 | 0 |
| B3E | 2 | -2/3 | 0 | 0 | 0 |
| S | 6 | -2 | 0 | 0 | 0 |
Последнее представление - сумма двух первых представлений. Т.о в группе Td имеется еще два независимых неприводимых трехмерных представления T1 и T2.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!