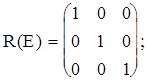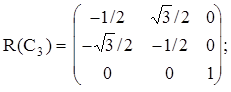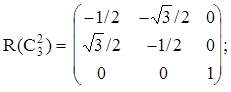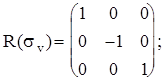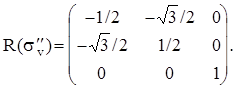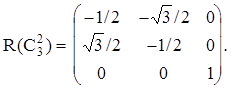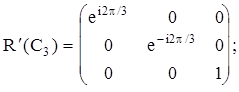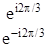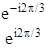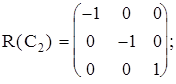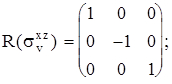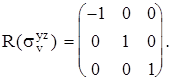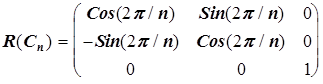 .
. 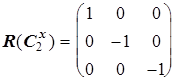 .
.
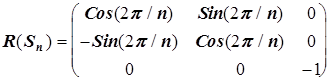 .
.
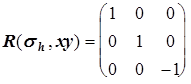 .
. 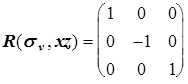 .
.
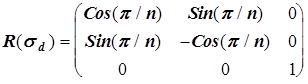 . p/n - угол относительно оси ОХ.
. p/n - угол относительно оси ОХ.
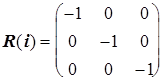 .
. 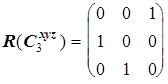 .
.
Непрерывные точечные группы.
Линейные молекулы обладают цилиндрической симметрией и имеют бесконечное число осей симметрии. Поворот на бесконечно малый угол обозначается как C¥. Наличие осей C¥ требует бесконечного числа плоскостей sv. Соответствующая группа обозначается как C¥v. Если существует бесконечное число осей C2, перпендикулярных C¥, то группа обозначается D¥h.
Самая высокая симметрия трехмерной системы - сферическая. Группа описывающая сферическую симметрию R(3), генераторами которой являются 3 любые взаимоперпендикулярные оси. Группа Rh(3) возникает из группы R(3) при добавлении еще одного генератора - операции инверсии. Все остальные точечные группы являются подгруппами групп R(3) или Rh(3).
Лекция 4.
Отображения, морфизмы.
Часто бывает полезно представить элементы некоторой группы другими величинами, удовлетворяющими той же таблице произведений, что и заданная группа. Это означает, что данная группа отображается в новую группу, причем каждый элемент в первоначальной группе имеет образ в новой. При этом совсем не обязательно, чтобы различные элементы в первоначальной группе имеют различные образы в новой. Если различные элементы одной группы имеют различные образы в другой группе, то эти группы называются изоморфными. В противном случае - гомоморфными. В качестве примера рассмотрим отображения группы C4:
| C4
| E
| C4
| C2
| C42
|
|
| 1
| 1
| 1
| 1
|
|
| 1
| -1
| 1
| -1
|
|
| 1
| i
| -1
| -i
|
|
| 1
| -i
| -1
| i
|
Если в качестве группового произведения принять обычное умножение, то элементы каждого из 4-х отображений образуют группу. Первая группа имеет порядок 1, вторая - 2, две последние - 4. В первом случае 4 элемента первой группы отображаются в один, во втором два в один. Т.о. первые два - гомоморфизмы. В двух последних различным элементам первоначальной группы соответствуют различные образы в отображениях. Т.о. эти группы изоморфны.
Рассмотрим вновь молекулу NH3 и каждому элементу симметрии поставим в соответствие матрицу преобразования декартовых координат атомов.
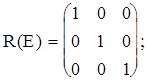
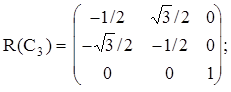
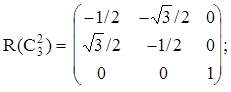
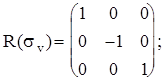

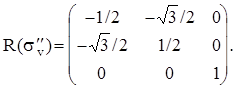
Матрицы, соответствующие операциям sv¢ и sv² , можно получить из произведения матриц R(C3 2 )R(sv) и R(C3)R(sv), соответственно, или через матрицу генератора sd при (p/n)=120o и (p/n)=-120o.
Из произведений матриц можно составить таблицу полностью идентичную таблице произведений элементов точечной группы C3v. Т.о. этот набор матриц образует группу изоморфную точечной группе C3v. Если существует множество матриц, представляющих собой группу и имеющих такую же таблицу произведений что и данная группа, то говорят, что эти матрицы порождают матричное представление (или просто представление) группы. Группа матриц, являющаяся представлением данной группы, не обязательно должна быть изоморфна последней. Матрицы могут быть одномерными, двумерными, трехмерными и т.д. Они могут быть действительными, комплексными и мнимыми. Единственное требование - они должны быть гомоморфны рассматриваемой группе и удовлетворять таблице произведений группы. Может существовать бесконечное множество возможных представлений. В том случае, если группа матриц изоморфна точечной группе, то они образуют точное представление группы.
Однако подробное и полное изложение теории представлений является предметом отдельного специального курса. Здесь речь пойдет лишь о тех понятиях теории представлений, которые будут необходимы для практического применения теории групп. Одной из основных задач, возникающих при поиске представлений групп, является определение так называемых неприводимые представлений. Неприводимые представления - матричные представления самой низшей размерности, которые нельзя преобразовать друг в друга. Неприводимые представления обладают следующими свойствами.
Если неприводимые представления одномерны, то они сами образуют группу.
Сумма квадратов размерностей неприводимых представлений равна порядку группы.
Число различных неприводимых представлений группы равно числу ее классов.
Рассмотрим группу C2 {E, C2}. Матрицы соответствующие операциям симметрии имеют вид:
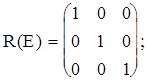

Эти матрицы образуют представление группы C2. Однако оно не является самым простым. Поскольку матрицы диагональны, то x, y и z координаты преобразуются независимо друг от друга. Рассматривая только эти компоненты получим три независимых отображения группы C2:
|
| E
| C2
|
| G(x)
| 1
| -1
|
| G(y)
| 1
| -1
|
| G(z)
| 1
| 1
|
Т.к. базисные вектора декартовой системы взаимноортогональны, то эти отображения взаимонезависимы. В отдельности - это неприводимые представления группы C2. Числа, выражающие эти представления, называются характерами. Характер - след матрицы, соответствующей данной операции симметрии. Здесь представления G(x) и G(y) совпадают и, следовательно, у группы C2 есть только два одномерных неприводимых представления. Таблица характеров неприводимых представлений для группы C2 имеет вид:
Таблица характеров включает в себя характеры для различных операций в каждом неприводимом представлении.
Рассмотрим группу C3 {E, 2C3}. Матрицы соответствующие операциям симметрии имеют вид:
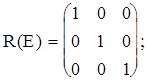
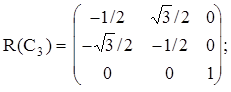
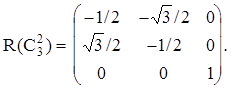
Матрицы, соответствующие операциям поворота, недиагональны. Т.о. x и y компоненты взаимозависимы. Следовательно из нельзя использовать отдельно для построения представлений. Однако z-компонента порождает независимое представление. Еще одно представление дают квадратные матрицы 2-го порядка, описывающие взаимное преобразование координат x и y. Это будет также неприводимое представление. Таблицу характеров можно записать двумя способами. Первый - через следы матриц:
Второй способ - диагонализация матриц. В результате приведения матриц, описывающих повороты, к диагональному виду получим новые матрицы:
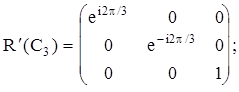

Два первых диагональных элемента являются комплексносопряженными. Двумерное представление можно разложить на два мнимых одномерных и таблицу характеров записать в виде:
Порядок группы - 3. Размерности представлений 12 + 12 + 12 = 3. Для циклических групп рассматриваются мнимые представления.
Группа C2v {E, C2, svx z, svy z}. Матрицы операций симметрии:
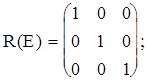
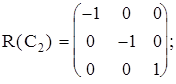
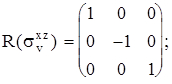
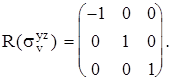
Матрицы диагональны, т. о. получим таблицу представлений:
|
| E
| C2
| svx z
| svy z
|
| G(x)
| 1
| -1
| 1
| -1
|
| G(y)
| 1
| -1
| -1
| 1
|
| G(z)
| 1
| 1
| 1
| 1
|
Однако в соответствии со свойствами представлений должно быть 4 неприводимых представления. Четвертое находится на основании свойства: G(a)´ G(b)= G(c) [ai´bi=ci]. Т.о.
G(z)´ G(x)={1 -1 1 -1 }=G(x)
G(z)´ G(y)={1 -1 -1 1 }=G(y)
G(x)´ G(y)={1 1 -1 -1 } ® новое представление.
В результате таблица характеров для группы C2v примет вид:
|
| E
| C2
| svx z
| svy z
|
| A1
| 1
| 1
| 1
| 1
|
| A2
| 1
| 1
| -1
| -1
|
| B1
| 1
| -1
| 1
| -1
|
| B2
| 1
| -1
| -1
| 1
|
В итоге мы имеем:
группа C2 - 2 представления - 2 вектора в двухмерном пространстве;
группа C3 - 1 одномерное и 1 двухмерное представления - 3 вектора в
трехмерном пространстве;
группа C2v - 4 одномерных представления - 4 вектора в четырехмерном
пространстве.
Т.о. неприводимые представления описывают элементы симметрии в n -мерном пространстве, построенном на системе n независимых базисных векторов.
Лекции 5-6.



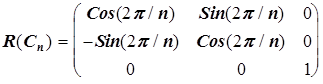 .
. 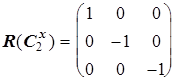 .
.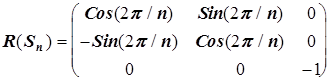 .
.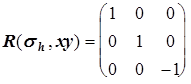 .
. 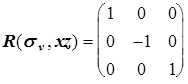 .
.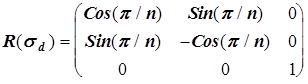 . p/n - угол относительно оси ОХ.
. p/n - угол относительно оси ОХ.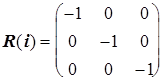 .
. 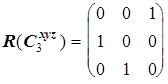 .
.