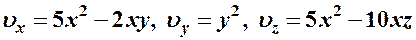Формула дифференцирования по времени
интеграла по подвижному объёму
Формулировка закона сохранения массы для
неподвижного пространственного объёма
Формула Гаусса-Остроградского.
Дивергенция вектора.
Дифференциальное уравнение неразрывности
- следствие закона сохранения массы
Уравнение неразрывности для несжимаемой среды
В этом разделе курса мы будем
Формулировать так называемые универсальные, то есть
Верные для любых сред, физические «законы сохранения»
Выводить из этих законов уравнения, связывающие различные параметры движущейся среды.
А именно, мы будем рассматривать следующие законы:
1. закон сохранения массы;
2. закон сохранения количества движения (импульса);
3. закон сохранения момента количества движения;
4. закон сохранения энергии (I закон термодинамики);
Закон изменения энтропии (II закон термодинамики).
Закон сохранения массы (ЗСМ)
Этот закон формулируется следующим образом.
Масса 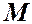 индивидуального объёма, т.е. объёма, состоящего из одних и тех же материальных частиц, постоянна:
индивидуального объёма, т.е. объёма, состоящего из одних и тех же материальных частиц, постоянна:
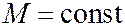 или
или 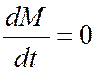 .
.
В МСС используется другая формулировка, в которую входит плотность 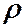 .
.
Пусть в объеме  содержится масса
содержится масса 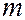 , тогда
, тогда 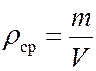 .
.
Для малого объёма 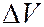 с массой
с массой 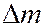 имеем:
имеем: 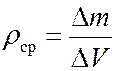
 .
.
Плотность в точке определяется формулой
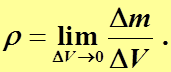
Здесь  означает, что
означает, что 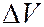 стягивается к
стягивается к
Рассматриваемой точке.
Последняя формула записывается также в виде
 ,
,
(правая часть - просто отношение бесконечно малых величин, а не производная 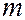 по
по  !).
!).
Масса бесконечно малой частицы: 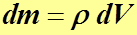 .
.
Масса в объеме  :
:
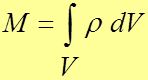 .
.
Математическая формулировка закона сохранения массы:
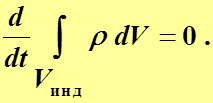 (2.1)
(2.1)
Обозначение 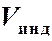 подчеркивает, что речь идет об индивидуальном объеме. При движении форма и величина
подчеркивает, что речь идет об индивидуальном объеме. При движении форма и величина 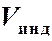 в общем случае меняются со временем.
в общем случае меняются со временем.
2.2. Формула дифференцирования по 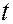 интеграла
интеграла
По подвижному объёму
Требуется вычислить  .
.
По определению производной по времени имеем
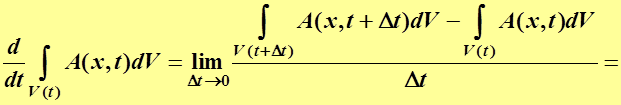
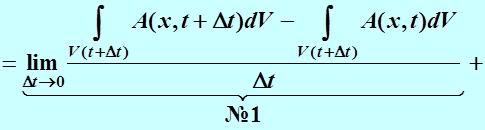

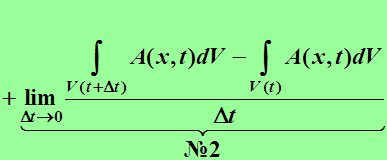
(прибавили и вычли в числителе член 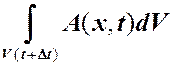 ).
).
Слагаемое №1: 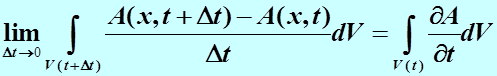 .
.
Слагаемое №2:  ,
,
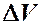 =
= 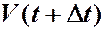 -
- 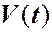
Вычисление слагаемого №2

Фиг. 2.1. Подвижный объем в моменты 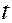 и
и 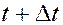
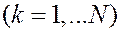 .
.
 - сумма малых объемов
- сумма малых объемов 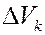 ;
; 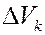 - цилиндр,
- цилиндр,
площадь его основания 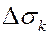 , высота
, высота  ,
,
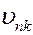 - проекция
- проекция  на нормаль
на нормаль 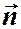 ,
,  .
. 
Интеграл по  приближенно равен следующей сумме
приближенно равен следующей сумме
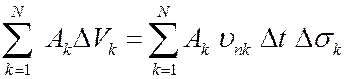 ,
,
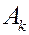 - значение
- значение 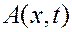 в некоторой точке площадки
в некоторой точке площадки 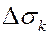 .
.
При 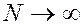 и
и  суммы в левой и правой частях этого равенства переходят в интегралы по
суммы в левой и правой частях этого равенства переходят в интегралы по  и
и 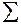 :
:
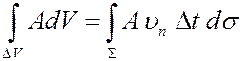 ,
,
Тогда получаем выражение для слагаемого №2:
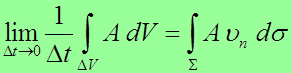 .
.
Итак, формула дифференцирования по 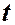 интеграла по подвижному объёму
интеграла по подвижному объёму 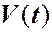 такова:
такова:
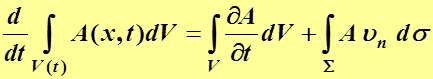 (2.2)
(2.2)
Формулировка закона сохранения массы (ЗСМ)
Для неподвижного пространственного объема
По формуле (2.2) при 
 .
.
Поэтому закон сохранения массы записывается в виде
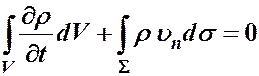 . (2.3)
. (2.3)
Соотношение (2.3) не содержит дифференцирования по 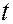 объемного интеграла. Поэтому в формуле (2.3) можно считать, что
объемного интеграла. Поэтому в формуле (2.3) можно считать, что  - неподвижный пространственный объём - область пространства, через которую протекает среда.
- неподвижный пространственный объём - область пространства, через которую протекает среда.


Фиг.2.2. Неподвижный пространственный объем
Тогда 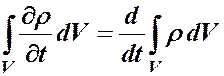 , и закон сохранения массы:
, и закон сохранения массы:
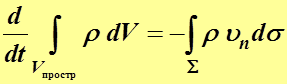 (2.4)
(2.4)
Это формулировка закона сохранения массы для пространственного объёма: увеличение массы в пространственном объёме за единицу времени равно массе, которая за это время втекает в объём.
Координат.
Компоненты нормали к поверхности 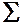 :
:
 , так как
, так как  .
.
Формула Г- О (другой вид):
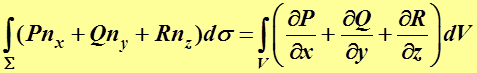 (2.5)
(2.5)
Если  , то (формула Г – О)
, то (формула Г – О)
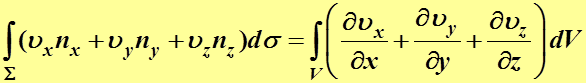
Или
 (2.6)
(2.6)
Пояснение к формуле (2.6)
1. Скалярное произведение двух векторов  и
и  в декартовых координатах:
в декартовых координатах:
 .
.
 .
.
2. Дивергенция любого вектора  с компонентами
с компонентами  обозначается
обозначается  . В декартовых координатах
. В декартовых координатах  определяется формулой
определяется формулой
 .
.
Уравнение неразрывности
Из закона сохранения массы.
Вывод.
В законе сохранения массы (2.3)
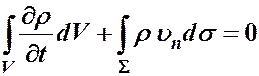
Или
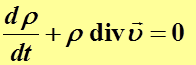 (2.10)
(2.10)
То есть соотношение

Задача
Дано поле скорости: 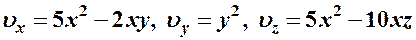
Формула дифференцирования по времени
интеграла по подвижному объёму



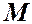 индивидуального объёма, т.е. объёма, состоящего из одних и тех же материальных частиц, постоянна:
индивидуального объёма, т.е. объёма, состоящего из одних и тех же материальных частиц, постоянна: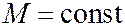 или
или 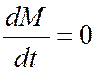 .
.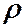 .
. содержится масса
содержится масса 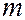 , тогда
, тогда 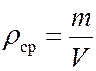 .
.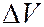 с массой
с массой 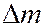 имеем:
имеем: 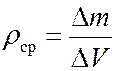
 .
.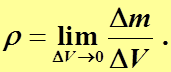
 означает, что
означает, что  ,
, !).
!).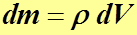 .
.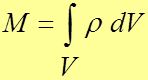 .
.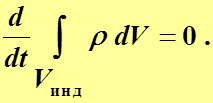 (2.1)
(2.1) подчеркивает, что речь идет об индивидуальном объеме. При движении форма и величина
подчеркивает, что речь идет об индивидуальном объеме. При движении форма и величина  интеграла
интеграла .
.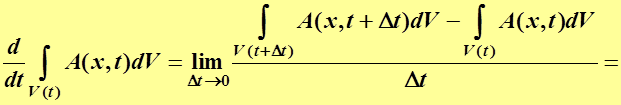
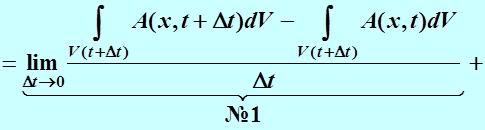
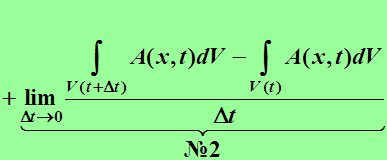
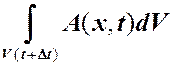 ).
).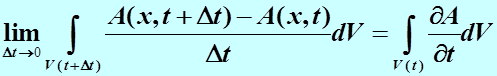 .
. ,
,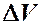 =
= 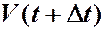 -
- 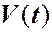

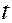 и
и 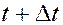
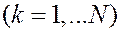 .
. - сумма малых объемов
- сумма малых объемов 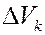 ;
; 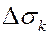 , высота
, высота  ,
,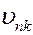 - проекция
- проекция  на нормаль
на нормаль 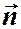 ,
,  .
. 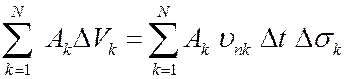 ,
,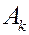 - значение
- значение 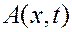 в некоторой точке площадки
в некоторой точке площадки  и
и  суммы в левой и правой частях этого равенства переходят в интегралы по
суммы в левой и правой частях этого равенства переходят в интегралы по  :
: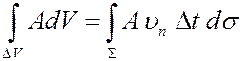 ,
,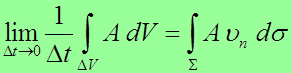 .
.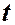 интеграла по подвижному объёму
интеграла по подвижному объёму 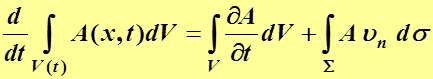 (2.2)
(2.2)
 .
.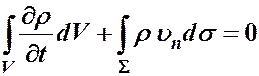 . (2.3)
. (2.3)

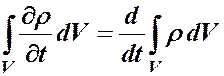 , и закон сохранения массы:
, и закон сохранения массы: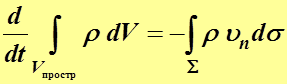 (2.4)
(2.4)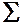 :
: , так как
, так как  .
.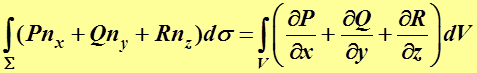 (2.5)
(2.5) , то (формула Г – О)
, то (формула Г – О)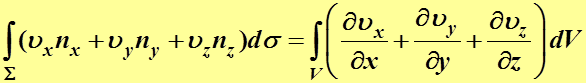
 (2.6)
(2.6) и
и  в декартовых координатах:
в декартовых координатах: .
. .
. с компонентами
с компонентами  обозначается
обозначается  . В декартовых координатах
. В декартовых координатах  .
.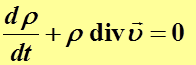 (2.10)
(2.10)