Свободные и связанные переменные.

λх.А - переменная х связана в выражении с А.

Определение.

х входит связанно в (АВ) тогда и только тогда, когда х входит связанно в А или связанно в B.

Определение.

х входит связанно в λу.А тогда и только тогда, когда (х ≡ у и х 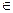А) или х входит связанно в А.

На место свободной переменной возможна подстановка.

Определение.

Свободные переменные - это синтаксические объекты, встречающиеся обычно в некотором контексте, вместо которых можно подставлять другие синтаксические объекты.

Связанные переменные не допускают подстановки.

(λх.х)+у Можем что-либо подставить на место у и не можем подставить на место х.

 

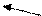
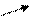Пример.      х+((λх.х)3)

         свободная                   связанная

 

Подстановка.

Определение.

Для 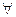термов М и N и 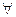переменной х результат подстановки [N/x]M -“ N на место х в М” определяется по индукции по построению терма М.

[N/x] x = N

[N/x] a = a

[N/x](M₁M₂) = ([N/x] M₁)([N/x] M₂)

[N/x](λх.M) = λх.M (т.к. х - связана)

[N/x](λу.M) = (λу.[N/x]М), если у ≠ х, у 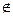N (или х 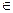М), иначе

   =^(α)(λz.[N/x][z/y]M),

если у ≠ х, у 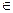N и x 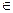M, где z- новая переменная, не входящая ни в N, ни в М.

   Это запрещает значению [N/x](λх.M) зависеть от связанной переменной у.

Пример. [3/y](y) →3

           [3/y](x) →x

           [3/y](y+x) →3+x

           [3/y](λу.y)7+x+y) → ((λу.y)7+x+3)

 

             ┌───║───_↓

           λу.((λу.y)7+x+y)3)

            ↑

┌─_↓

 (λу.y+34) (λx.x) →((((λx.x)+)3)4) →((+3)4)

^↑──────└───┘ ^↑──┘      

                                                       

                                                       ┌───_↓                   ┌───_↓

Пример. (λx. λу. λz+ x(-yz))123→(λxyz.+x(-yz))123→((λyz.+1(-yz))2)3→

                                                        ↑_________│        ↑_______│

   |    ↓

→(λz.+1(-2z))3→+1(-23)

  ↑             

 

Вначале вычисляется выражение в скобках.

 

Коллизия имен переменных.

Чтобы ввести новые имена используется α - конверсия, она позволяет изменять имена свободной переменной x.

(х+(λx.-х3)2)  не сможет дать какую-либо характеристику переменной.

Использование (α) - конверсии позволит изменить имя свободной переменной.

(х+(λx.-х3)2) 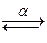 (у+(λx.-х3)2) получим свободное вхождение у и связное вхождение х.

Изменение статуса переменной при подстановке называется коллизией переменных.

Коллизия переменных может служить источником ошибок в вычислениях.

Пример

Прямая редукция терма (λxy.x)y дает неверный результат

(λxy.x)y →^(β) λy.y,

а если предварительно переименовать связанную переменную y, получится верный результат:

(λxy.x)y →^(α) (λxz.x)y →^(β) λz.y ≠ λy.y.

 

Редукция

Определение.

Х сворачивается к Y 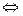Y -результат замены части Х вида (λх.M)N на [N/x]M:

X редуцируется к Y 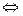Y получается из Х с помощью конечной (возможно, пустой) последовательности сворачиваний и замен имен связанных переменных.

Выражение вида (λх.M)N называется редекс.

Подстановка N на место х в М [N/x]M называется сверткой.

λ выражение Р находится в нормальной форме, если не содержит ни одного редекса.

 

Пример. 1) λх.х - является нормальной формой

            2)(λх.+х((λу.у)х)) → не является нормальной формой → (λх.+хх) - является нормальной формой.

Говорят, что терм Р редуцируется к терму Q, если существует доказательство такого выражения: Р → Q.

Теорема Черча-Россера:

Если х конвертируется к у, т.е. х у (х редуцируется к у: х→у) и х конвертируется (редуцируется) к z,то а: у→а и z→а (у а и z а)

 Следствие:

У 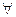λ - терма ! (единственная) нормальная форма.

Доказательство: (от противного)

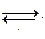Пусть у выражения x существует две нормальные формы a,b: х→a и х→b т.е. а,b (a ≠b): (a b)

                                                                                                          

По Т h C: a→c, b→c т.к. а может редуцироваться, то а не является нормальной        формой, то же самое можно сказать про b.

Либо не редуцируются, либо совпадают.

Двух нормальных форм существовать не может. #

Если а редуцируется к b (а→b) и b редуцируется к а (b→a),то говорят что а и b

конвертируются одно в другое (а b),т.е. а→b, b→a: а b- взаимно конвертируются.

Теорема.

λ–теория не противоречива, т.е. в ней нельзя вывести любые утверждения.

 

Теорема: (О комбинаторной полноте).

Пусть λ- терм М содержит n свободных переменных х₁…х_n, тогда  λ-терм F: х₁…x_n не являются свободными переменными F (X₁…X_n FV(F)) и при этом FX₁…X_n=M соответственно F=λx₁…x_n.M.

 

Погружение классических вычислений в λ-исчисление.

Определение:

Нумералы - объекты, обладающие свойствами натуральных чисел.

                    n = λxy.(xⁿ)y   n =(SB)ⁿ(KI), здесь S,B,K,I - простейшие комбинаторы

Системы комбинаторов предназначены для выполнения тех же функций, что и системы

-l - конверсии

B: Bfgx = f(gx)- элементарный композитор

S: Sfgx = fx(gx) –элементарный коннектор

K: Kcx =c – элементарный канцелятор

I: Ix = x – комбинатор тождества

 

Пусть z₀= λyx.x (считаем это число нулем). Остальные целые числа введем по индукции: z_n+1=σz_n, где σ - функция добавления единицы: σ = λxyz.y(xyz)

Операция сложения PLUS:

PLUS = λxy.xσy

Утверждается, что PLUSz₀b=b и PLUS(σa)b=σ(PLUSab) (проверяется подстановкой).

Определение:

Усеченная разность: DIF=λxу.yπx, где π-функция предшествования

                                 π=λx.хω(kz₀)z₁, где ω= λx.D(σ(xz₀))(xz₀) πz_i+1=z_i, i ≥ 0

                                           k= λxy.x                                           πz₀=z₀.

D - декартово замкнутое произведение.

D: PROD = λxy.x(yσ)z₀

TRUE λxy.x (так обозначим)

FALSE  λxy.y

If X then Y else Z  XYZ.

 

Нумералы.

Введем по индукции обозначение

aⁿb                       n 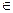N                                                 n ab= aⁿb

a⁰b=b

aⁿ⁺¹b=a(aⁿb)

Пример. a³b=a(a(ab))

 

Определение:

Нумераломn будем называть λ-выражение вида λху.хⁿy, где n=0,1,2,…

n = λху.хⁿy

n =(SB) ⁿ(KI) (то же выражение, но в терминах комбинаторной логики)

Введем функцию прибавления единицы σ.

σ = λхуz.y(хyz) (σ = λхуz.xy(yz))

σn = n+1

Пример. 0 = λху.y 2 = λху.x(xy)

Покажем, что для таких нумералов (n) σ прибавляет единицу:

                                                          ┌───────_↓

σ n ab = (λхуz.y(xyz))(λху.хⁿy)ab = (((λx.(λy.(λz.y(xyz))))(λx.λy.хⁿy))a)b                                                                   └───_σ──┘└── _n ─┘          ^↑───────────└─────┘

  ┌────_↓───────_↓                   ┌─────────_↓

= ((λy.(λz.(y((λx.λy.хⁿy)yz)))a)b = (λz.a((λx.λy.хⁿy))az))b = a((λx.λy.хⁿy)ab) =

      ^↑──────────────┘     ^↑──────────┘   └─ _n ───┘

= a(aⁿb) =aⁿ⁺¹b = /(λху.хⁿ⁺¹y)ab/ = (n+1) ab.

                                                              ½       ↓

σ (SB) ⁿ(KI) = (λхуz.y(xyz))((SB) ⁿ(KI))(λхуz.y(xyz))[(SB) ⁿ(KI)]ab =

                                                               ^↑──────└─────┘

= a(((SB) ⁿ(KI)a)b) =^B Ba[(SB) ⁿ(KI)a]b =^S SB[(SB) ⁿ(KI)]ab = (SB) ⁿ⁺¹(KI)ab

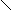 └_a┘└──_b───┘_{c x z}└──_y──┘ _z

σ^| = λхуz.xy(yz)- альтернативное определение σ, которое также приводится в литературе. Для него можно провести аналогичные выводы.

TRUE λху.x

FALSE λху.y

If x then y else z xyz

Как это проверить?

If TRUE then A else B  A

If FALSE then A else B   B

┌─_↓

(λху.x)AB = A

 

┌─_↓

(λху.y)AB = B

 

 

X&Y If X then Y else FALSE

XVY If X then TRUE else Y

 

Рекурсия

Определение:

Рекурсивное определение - это определение, которое внутри себя содержит ссылку

на определяемый объект.

Пример. 1) Факториал ƒac(x): x*ƒac(x-1),

                if (х=0) then 1      ƒac(0)=1.

                else x* ƒac(x-1)

              2) Список:                                                            

                                                                           Голова                              

cons(x.y)→(x.y) (точечная пара)

head(x.y) →x     (голова)                                                                                  

nil

tail(x.y) → y      (хвост)                                                                                                        

 length(x)                                                                                                           

 tail(x) = Nil                                                                                                                   

 length(x) = 1+ length(tail(x))

 length(x): if x = Nil then 0

else 1+(length(tail(x))).

 

Рекурсия в λ-исчислении.

Определение.

Выражение х является неподвижной точкой функции ƒ, если х = ƒх.

Теорема: (О неподвижной точке).

           1)Для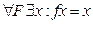

           2) -позволяет определить неподвижную точку.

                    ↑обьект       ↑неподвижная точка

Пример. Y = λƒ.(λx.ƒxx)(λx.ƒxx)

            YH = …H(YH)

# w = λx.ƒxx – введем этот объект и скажем, что х = ww =

┌──_↓─_↓

= (λх.ƒ(x x))(λx.ƒ(xx)) = ƒ((λx.ƒ(xx))(λx.ƒ(xx))) = ƒ(x) 1) доказано. #

↑                

Определение.

Комбинатор неподвижной точки - это терм М: 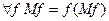, т.е. Мƒ - неподвижная точка.

Используется для выражения рекурсии в чистом виде (без самоссылки), т.к. в λ-исчислении не предусмотрено именование функций.

 

Пример. θ = (λxу.(у(хху))(λxу.у(хху))

С помощью комбинатора Y запишем и вычислим комбинатор какого-либо числа.

ƒac: λx.(if x=0,1,x* ƒac(-x1)) (λx.IF(=x0)1(*ƒac(-x1))

Вычислим факториал от 2: ƒac= λx.(… ƒac …).

Применяя λ - абстракцию, получим ƒac(2) λƒac1.ƒacƒac1= (λƒac1.(λх.(… ƒac1…)))ƒac

Введем дополнительную функцию H, которая в определении факториала позволяет абстрагироваться от определения факториала.

По правилу (η) λƒac1.ƒacƒac1=ƒac и  ƒac= λƒac1.(λх.(…ƒac1…)))ƒac.

H=λƒac1.(λх.(IF x=0,1,x*ƒac1(-x1))

ƒac=Hƒac YH=H(YH)

               

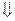
         ƒac2=YH2

Шаг за шагом произведем эти вычисления.

┌───_↓─────_↓

(λƒ.(λх.ƒхх)(λх.ƒхх))(λƒac.(λn.(if n=0,1,n*ƒac(n-1))))2 ((λƒac.(λn.(if n=0,1,

n*ƒac(n-1))))(YH))2 (λn.(if n=0,1,n*(YH)(n-1)))2 if (2=0),1,2*(YH)(2-1)

2*((YH)1) 2*[H(YH)1] 2*[(λƒac.λn.if n=0,1,n_*ƒac(n-1))(YH)1]

2*[ if 1=0,1,1*(YH)(1-1)] 2*[1*(YH0)] 2*1*(YH0)

2*1*[H(YH)0] 2*1*[(λƒacn.if n=0,1,n_*ƒac(n-1))(YH)0]

2*1*[ if 0=0,1,n*[(YH)(0-1)]] 2*1*1=2.

 

Определения:

Бестиповое λ - исчисление является синтактико-семантической системой, т.е. семантика выражения полностью определяется его синтаксисом.

Синтаксис - способ записи выражения.

Семантика – смысл выражения. Алгоритм вычисления выражения полностью определяется способом его записи.

Все вычисления в символьных системах сводятся к подстановке одних идентификаторов вместо других, при этом они вначале вычисляются в среде, результат вычисления выражения изменяет исходную среду на новую.

Контрольные вопросы

1. Дайте определение формальной системы.
2. Приведите примеры символов и термов в λ–исчислении.
3. На основании каких постулатов λ–исчисления можно избавиться от коллизии переменных?
4. Какие аксиомы и правила вывода λ–исчисления позволяют применить функцию к ее аргументам?
5. На основании каких положений доказывается единственность нормальной формы?
6. С помощью каких средств могут быть заданы алгоритмы, использующие примитивную рекурсию?