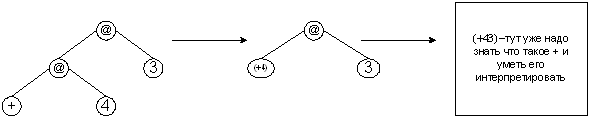Аппликативные вычисления в теории алгоритмов
Утверждено
редсоветом института
в качестве
учебного пособия
Москва 2003
УДК 681.3
Гаврилов А.В. Аппликативные вычисления в теории алгоритмов: Учебное пособие. М.:МИФИ, 2003. – 48 с.
Учебное пособие дает базовые сведения по теории алгоритмов.
Подробно рассматриваются основы построения и использования формальных систем, ламбда-исчисление и комбинаторная логика, основы теории абстрактных машин.
Основной упор делается на использование полученных теоретических знаний при решении конкретных алгоритмических задач. На примере категориальной абстрактной машины демонстрируются методы формальной реализации и верификации конструкций языков программирования и объектной модели.
Полученные навыки позволяют проводить проектирование, анализ и реализацию формальных моделей для конкретных алгоритмических задач, грамотно специфицировать корректное решение.
Учебное пособие "Дискретная математика" является базовым в специальной математической подготовке инженера-математика и предназначено для изучения студентами соответствующих специальностей (факультеты «К», «А», «Б» МИФИ).
Содержание
Аппликативные вычисления в теории алгоритмов. 1
Содержание. 3
Введение. 5
Построение λ- теории. 6
Основы теории формальных систем. 6
Понятие λ-исчисления. 7
Построение бестипового λ-исчисления. 7
Свободные и связанные переменные. 8
Подстановка. 9
Коллизия имен переменных. 10
Редукция. 10
Погружение классических вычислений в λ-исчисление. 12
Нумералы. 13
Рекурсия. 14
Рекурсия в λ-исчислении. 15
Контрольные вопросы.. 16
Бестиповая комбинаторная логика. 17
Комбинаторы. 17
Построение комбинаторной логики. 18
Базис K,S. 19
Базис I,B,C,S. 20
Преимущества комбинаторов. 20
Контрольные вопросы.. 20
Типизированные системы. 21
Использование типов. 21
Приписывание типа комбинатору неподвижной точки. 22
Вычисление выражений при помощи комбинаторной логики. 22
Контрольные вопросы.. 22
Реализация языков программирования. 23
Общая схема реализации функциональных языков. 23
Расширенное λ-исчисление. 24
Редукция графа. 25
Алгоритм редукции графа (РГ) 26
Суперкомбинаторы. 27
Алгоритм приведения λ-выражения к суперкомбинаторному виду. 28
Упорядочивание параметров. 29
Способы реализации рекурсии. 30
Контрольные вопросы.. 32
Компиляция в коды абстрактных машин. 33
Кодирование по де Брейну. 33
Алгоритм преобразования λ-выражений по де Брейну. 34
Семантические равенства для кодов де Брейна: 35
Категориальная комбинаторная логика (ККЛ). 36
Общие свойства абстрактных машин. 37
Категориальная абстрактная машина (КАМ). 38
Цикл работы КАМ... 39
Оптимизация кода КАМ... 40
Дополнительные функциональные инструкции. 41
Рекурсия в КАМ... 41
Схема трансляции терма расширенного λ-исчисления в код КАМ... 41
Пример вычисления выражений на КАМ... 42
Контрольные вопросы.. 45
Смешанные вычисления. 46
Процедура смешанных вычислений. 46
Трансформационные семантики. 48
Проекции Футамуры.. 50
Контрольные вопросы.. 50
ЛИТЕРАТУРА.. 51
Введение
Использование аппликативных вычислений при решении разнообразных задач создания программного обеспечения давно признано мощным и полезным подходом к разработке сложных систем. Широкий спектр систем текстовых преобразований, символьных вычислений, систем декларативного программирования основаны на применении механизмов аппликативных вычислений для решения конкретных прикладных задач.
При этом аппликативный подход хорошо формализуем в рамках теории алгоритмов средствами ламбда-исчисления и его специализированного варианта – комбинаторной логики. Наличие строгого математического аппарата позволяет разработчику, с одной стороны, проверить корректность реализации своих моделей, а с другой – обеспечить формальное проектирование новых средств и алгоритмов.
Более того, решение сложных задач часто предполагает использование разнородных языковых средств реализации специализированных подсистем. Предлагаемый подход обеспечивает единую среду вычислений, основанную на совместном использовании общей абстрактной машины и единой объектной системы. Математически обоснованная обобщенная схема трансляции гарантирует корректность реализации каждого языка в рамках интегрированной вычислительной среды.
Таким образом, использование средств аппликативных вычислений при проектировании сложных прикладных систем позволяет разработчику не только получить адекватное решение комплексных задач обработки информации, но и проверить его корректность формальными методами.
Автор выражает благодарность за помощь в создании данного учебного пособия Колычеву В.Д., Гольцеру Ю.Я., Гусаровой Т.Н.
Построение λ- теории
Определение.
х входит связанно в (АВ) тогда и только тогда, когда х входит связанно в А или связанно в B.
Определение.
х входит связанно в λу.А тогда и только тогда, когда (х ≡ у и х  А) или х входит связанно в А.
А) или х входит связанно в А.
На место свободной переменной возможна подстановка.
Определение.
Свободные переменные - это синтаксические объекты, встречающиеся обычно в некотором контексте, вместо которых можно подставлять другие синтаксические объекты.
Связанные переменные не допускают подстановки.
(λх.х)+у Можем что-либо подставить на место у и не можем подставить на место х.
 Пример. х+((λх.х)3)
Пример. х+((λх.х)3)
свободная связанная
Подстановка.
Определение.
Для 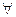 термов М и N и
термов М и N и 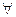 переменной х результат подстановки [N/x]M -“ N на место х в М” определяется по индукции по построению терма М.
переменной х результат подстановки [N/x]M -“ N на место х в М” определяется по индукции по построению терма М.
[N/x] x = N
[N/x] a = a
[N/x](M1M2) = ([N/x] M1)([N/x] M2)
[N/x](λх.M) = λх.M (т.к. х - связана)
[N/x](λу.M) = (λу.[N/x]М), если у ≠ х, у 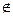 N (или х
N (или х 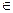 М), иначе
М), иначе
=(α)(λz.[N/x][z/y]M),
если у ≠ х, у 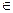 N и x
N и x 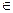 M, где z- новая переменная, не входящая ни в N, ни в М.
M, где z- новая переменная, не входящая ни в N, ни в М.
Это запрещает значению [N/x](λх.M) зависеть от связанной переменной у.
Пример. [3/y](y) →3
[3/y](x) →x
[3/y](y+x) →3+x
[3/y](λу.y)7+x+y) → ((λу.y)7+x+3)
┌───║───↓
 λу.((λу.y)7+x+y)3)
λу.((λу.y)7+x+y)3)
 ↑
↑
┌─↓
(λу.y+34) (λx.x) →((((λx.x)+)3)4) →((+3)4)
↑──────└───┘ ↑──┘
┌───↓ ┌───↓
Пример. (λx. λу. λz+ x(-yz))123→(λxyz.+x(-yz))123→((λyz.+1(-yz))2)3→
↑_________│ ↑_______│
 | ↓
| ↓
 →(λz.+1(-2z))3→+1(-23)
→(λz.+1(-2z))3→+1(-23)
 ↑
↑
Вначале вычисляется выражение в скобках.
Коллизия имен переменных.
Чтобы ввести новые имена используется α - конверсия, она позволяет изменять имена свободной переменной x.
(х+(λx.-х3)2)  не сможет дать какую-либо характеристику переменной.
не сможет дать какую-либо характеристику переменной.
Использование (α) - конверсии позволит изменить имя свободной переменной.
(х+(λx.-х3)2) 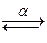 (у+(λx.-х3)2) получим свободное вхождение у и связное вхождение х.
(у+(λx.-х3)2) получим свободное вхождение у и связное вхождение х.
Изменение статуса переменной при подстановке называется коллизией переменных.
Коллизия переменных может служить источником ошибок в вычислениях.
Пример
Прямая редукция терма (λxy.x)y дает неверный результат
(λxy.x)y →(β) λy.y,
а если предварительно переименовать связанную переменную y, получится верный результат:
(λxy.x)y →(α) (λxz.x)y →(β) λz.y ≠ λy.y.
Редукция
Определение.
Х сворачивается к Y 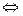 Y -результат замены части Х вида (λх.M)N на [N/x]M:
Y -результат замены части Х вида (λх.M)N на [N/x]M:
X редуцируется к Y 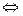 Y получается из Х с помощью конечной (возможно, пустой) последовательности сворачиваний и замен имен связанных переменных.
Y получается из Х с помощью конечной (возможно, пустой) последовательности сворачиваний и замен имен связанных переменных.
Выражение вида (λх.M)N называется редекс.
Подстановка N на место х в М [N/x]M называется сверткой.
λ выражение Р находится в нормальной форме, если не содержит ни одного редекса.
Пример. 1) λх.х - является нормальной формой
2)(λх.+х((λу.у)х)) → не является нормальной формой → (λх.+хх) - является нормальной формой.
Говорят, что терм Р редуцируется к терму Q, если существует доказательство такого выражения: Р → Q.
Теорема Черча-Россера:
Если х конвертируется к у, т.е. х  у (х редуцируется к у: х→у) и х конвертируется (редуцируется) к z,то
у (х редуцируется к у: х→у) и х конвертируется (редуцируется) к z,то  а: у→а и z→а (у
а: у→а и z→а (у  а и z
а и z  а)
а)
Следствие:
У 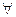 λ - терма
λ - терма  ! (единственная) нормальная форма.
! (единственная) нормальная форма.
Доказательство: (от противного)
Пусть у выражения x существует две нормальные формы a,b: х→a и х→b т.е.  а,b (a ≠b): (a
а,b (a ≠b): (a 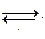 b)
b) 
По Т h  C: a→c, b→c
C: a→c, b→c  т.к. а может редуцироваться, то а не является нормальной формой, то же самое можно сказать про b.
т.к. а может редуцироваться, то а не является нормальной формой, то же самое можно сказать про b.
 Либо не редуцируются, либо совпадают.
Либо не редуцируются, либо совпадают.
 Двух нормальных форм существовать не может. #
Двух нормальных форм существовать не может. #
Если а редуцируется к b (а→b) и b редуцируется к а (b→a),то говорят что а и b
конвертируются одно в другое (а  b),т.е. а→b, b→a: а
b),т.е. а→b, b→a: а  b- взаимно конвертируются.
b- взаимно конвертируются.
Теорема.
λ–теория не противоречива, т.е. в ней нельзя вывести любые утверждения.
Теорема: (О комбинаторной полноте).
Пусть λ- терм М содержит n свободных переменных х1…хn, тогда  λ-терм F: х1…xn не являются свободными переменными F (X1…Xn
λ-терм F: х1…xn не являются свободными переменными F (X1…Xn  FV(F)) и при этом FX1…Xn=M соответственно F=λx1…xn.M.
FV(F)) и при этом FX1…Xn=M соответственно F=λx1…xn.M.
Погружение классических вычислений в λ-исчисление.
Определение:
Нумералы - объекты, обладающие свойствами натуральных чисел.
n = λxy.(xn)y n =(SB)n(KI), здесь S,B,K,I - простейшие комбинаторы
Системы комбинаторов предназначены для выполнения тех же функций, что и системы
-l - конверсии
B: Bfgx = f(gx)- элементарный композитор
S: Sfgx = fx(gx) –элементарный коннектор
K: Kcx =c – элементарный канцелятор
I: Ix = x – комбинатор тождества
Пусть z0= λyx.x (считаем это число нулем). Остальные целые числа введем по индукции: zn+1=σzn, где σ - функция добавления единицы: σ = λxyz.y(xyz)
Операция сложения PLUS:
PLUS = λxy.xσy
Утверждается, что PLUSz0b=b и PLUS(σa)b=σ(PLUSab) (проверяется подстановкой).
Определение:
Усеченная разность: DIF=λxу.yπx, где π-функция предшествования
π=λx.хω(kz0)z1, где ω= λx.D(σ(xz0))(xz0) πzi+1=zi, i ≥ 0
k= λxy.x πz0=z0.
D - декартово замкнутое произведение.
D: PROD = λxy.x(yσ)z0
TRUE  λxy.x (так обозначим)
λxy.x (так обозначим)
FALSE  λxy.y
λxy.y
If X then Y else Z  XYZ.
XYZ.
Нумералы.
Введем по индукции обозначение
anb n 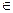 N n ab= anb
N n ab= anb
a0b=b
an+1b=a(anb)
Пример. a3b=a(a(ab))
Определение:
Нумераломn будем называть λ-выражение вида λху.хny, где n=0,1,2,…
n = λху.хny
n =(SB) n(KI) (то же выражение, но в терминах комбинаторной логики)
Введем функцию прибавления единицы σ.
σ = λхуz.y(хyz) (σ = λхуz.xy(yz))
σn = n+1
Пример. 0 = λху.y 2 = λху.x(xy)
Покажем, что для таких нумералов (n) σ прибавляет единицу:
┌───────↓
σ n ab = (λхуz.y(xyz))(λху.хny)ab = (((λx.(λy.(λz.y(xyz))))(λx.λy.хny))a)b └───σ──┘└── n ─┘ ↑───────────└─────┘
┌────↓───────↓ ┌─────────↓
= ((λy.(λz.(y((λx.λy.хny)yz)))a)b = (λz.a((λx.λy.хny))az))b = a((λx.λy.хny)ab) =
↑──────────────┘ ↑──────────┘ └─ n ───┘
= a(anb) =an+1b = /(λху.хn+1y)ab/ = (n+1) ab.
 ½ ↓
½ ↓
σ (SB) n(KI) = (λхуz.y(xyz))((SB) n(KI))(λхуz.y(xyz))[(SB) n(KI)]ab =
↑──────└─────┘
= a(((SB) n(KI)a)b) =B Ba[(SB) n(KI)a]b =S SB[(SB) n(KI)]ab = (SB) n+1(KI)ab
 └a┘└──b───┘c x z└──y──┘ z
└a┘└──b───┘c x z└──y──┘ z
σ| = λхуz.xy(yz)- альтернативное определение σ, которое также приводится в литературе. Для него можно провести аналогичные выводы.
TRUE λху.x
FALSE λху.y
If x then y else z xyz
Как это проверить?
If TRUE then A else B A
If FALSE then A else B B
┌─↓


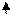

 (λху.x)AB = A
(λху.x)AB = A


┌─↓


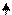
 (λху.y)AB = B
(λху.y)AB = B


X&Y If X then Y else FALSE
XVY If X then TRUE else Y
Рекурсия
Определение:
Рекурсивное определение - это определение, которое внутри себя содержит ссылку
на определяемый объект.
Пример. 1) Факториал ƒac(x): x*ƒac(x-1),
if (х=0) then 1 ƒac(0)=1.
else x* ƒac(x-1)


 2) Список:
2) Список:

 Голова
Голова


 cons(x.y)→(x.y) (точечная пара)
cons(x.y)→(x.y) (точечная пара)
head(x.y) →x (голова)
tail(x.y) → y (хвост)
length(x)
tail(x) = Nil
length(x) = 1+ length(tail(x))
length(x): if x = Nil then 0
else 1+(length(tail(x))).
Рекурсия в λ-исчислении.
Определение.
Выражение х является неподвижной точкой функции ƒ, если х = ƒх.
Теорема: (О неподвижной точке).
1)Для 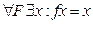
2)  -позволяет определить неподвижную точку.
-позволяет определить неподвижную точку.
↑обьект ↑неподвижная точка
Пример. Y = λƒ.(λx.ƒxx)(λx.ƒxx)
YH = …H(YH)
# w = λx.ƒxx – введем этот объект и скажем, что х = ww =
┌──↓─↓
= (λх.ƒ(x x))(λx.ƒ(xx)) = ƒ((λx.ƒ(xx))(λx.ƒ(xx))) = ƒ(x) 1) доказано. #

 ↑
↑
Определение.
Комбинатор неподвижной точки - это терм М: 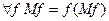 , т.е. Мƒ - неподвижная точка.
, т.е. Мƒ - неподвижная точка.
Используется для выражения рекурсии в чистом виде (без самоссылки), т.к. в λ-исчислении не предусмотрено именование функций.
Пример. θ = (λxу.(у(хху))(λxу.у(хху))
С помощью комбинатора Y запишем и вычислим комбинатор какого-либо числа.
ƒac: λx.(if x=0,1,x* ƒac(-x1)) (λx.IF(=x0)1(*ƒac(-x1))
Вычислим факториал от 2: ƒac= λx.(… ƒac …).
Применяя λ - абстракцию, получим ƒac(2) λƒac1.ƒacƒac1= (λƒac1.(λх.(… ƒac1…)))ƒac
Введем дополнительную функцию H, которая в определении факториала позволяет абстрагироваться от определения факториала.
По правилу (η) λƒac1.ƒacƒac1=ƒac и  ƒac= λƒac1.(λх.(…ƒac1…)))ƒac.
ƒac= λƒac1.(λх.(…ƒac1…)))ƒac.
H=λƒac1.(λх.(IF x=0,1,x*ƒac1(-x1))
ƒac=Hƒac YH=H(YH)
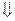
ƒac2=YH2
Шаг за шагом произведем эти вычисления.
┌───↓─────↓
(λƒ.(λх.ƒхх)(λх.ƒхх))(λƒac.(λn.(if n=0,1,n*ƒac(n-1))))2  ((λƒac.(λn.(if n=0,1,
((λƒac.(λn.(if n=0,1,
n*ƒac(n-1))))(YH))2  (λn.(if n=0,1,n*(YH)(n-1)))2
(λn.(if n=0,1,n*(YH)(n-1)))2  if (2=0),1,2*(YH)(2-1)
if (2=0),1,2*(YH)(2-1) 
 2*((YH)1)
2*((YH)1)  2*[H(YH)1]
2*[H(YH)1]  2*[(λƒac.λn.if n=0,1,n*ƒac(n-1))(YH)1]
2*[(λƒac.λn.if n=0,1,n*ƒac(n-1))(YH)1] 
 2*[ if 1=0,1,1*(YH)(1-1)]
2*[ if 1=0,1,1*(YH)(1-1)]  2*[1*(YH0)]
2*[1*(YH0)]  2*1*(YH0)
2*1*(YH0) 
 2*1*[H(YH)0]
2*1*[H(YH)0]  2*1*[(λƒacn.if n=0,1,n*ƒac(n-1))(YH)0]
2*1*[(λƒacn.if n=0,1,n*ƒac(n-1))(YH)0] 
 2*1*[ if 0=0,1,n*[(YH)(0-1)]]
2*1*[ if 0=0,1,n*[(YH)(0-1)]]  2*1*1=2.
2*1*1=2.
Определения:
Бестиповое λ - исчисление является синтактико-семантической системой, т.е. семантика выражения полностью определяется его синтаксисом.
Синтаксис - способ записи выражения.
Семантика – смысл выражения. Алгоритм вычисления выражения полностью определяется способом его записи.
Все вычисления в символьных системах сводятся к подстановке одних идентификаторов вместо других, при этом они вначале вычисляются в среде, результат вычисления выражения изменяет исходную среду на новую.
Контрольные вопросы
- Дайте определение формальной системы.
- Приведите примеры символов и термов в λ–исчислении.
- На основании каких постулатов λ–исчисления можно избавиться от коллизии переменных?
- Какие аксиомы и правила вывода λ–исчисления позволяют применить функцию к ее аргументам?
- На основании каких положений доказывается единственность нормальной формы?
- С помощью каких средств могут быть заданы алгоритмы, использующие примитивную рекурсию?
Комбинаторы.
Определение:
λ-выражение без свободных переменных называется комбинатором.
Позволяет избавиться от связанных переменных в λ-выражении.
Системы комбинаторов предназначены для выписывания тех же функций, что системы λ-конверсий, но без использования связанных переменных.
Пример. Ia = a
I: λx.x
Kab = a
K: λxy.x
Sabc = ac(bc)
S: λxyz.xz(yz)
Одни комбинаторы можно выражать через другие I = SKK.
Проверим это двумя способами.
1-ый способ:
Определение:
Комбинаторная характеристика – способ передачи информации об объекте в виде правил текстуального преобразования.
SKKa → Ka(Ka) → a
2-ой способ:
┌──↓ ┌─↓
(λxyz.xz(yz))(λxy.x)(λxy.x)→(λyz.(λxy.x)z(yz))(λxy.x)→((xy.z)(yz)→
↑─────────└────┘
→(λyz.z)(λxy.x)→ λz.z
Определение:
Базис формальной системы - минимальный набор объектов этой системы, через который можно с помощью аксиом и правил вывода выразить все остальные объекты формальной системы.
Определение:
Базисом бестиповой комбинаторной логики является набор комбинаторов: К,S и т.д.
Теорема Черча-Россера.
If А→В, А→С
then  D:B→D, C→D
D:B→D, C→D
Базис K, S.
Кроме базисного набора K, S будем использовать еще плюс к ним I.
Любое λ-выражение Р, не содержащее свободных переменных представляется в базисе IKS индукцией по построению терма Р.
Р: FV(P) = Ø –свободные переменные.
λх.х = I
λx.P = KP, если х 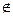 FV(P)
FV(P)
λx.PQ = S(λx.P)(λx.Q)
Примеры.
λxy.yx = S(K(SI))(S(KK)I)
Babc = a(bc) Представим комбинатор B в базисе I,K,S.
B: λxyz.x(yz)
Ый способ
λx.(λy.(λz.x(yz))) = λx.(λy.(S(λz.x)(λz.(yz))) = λx.λy.(S(Kx)(S(λz.y)(λz.z))) =
= λx.λy.((S(Kx)(S(Ky)I)) = λx.(S(λy.S(Kx))(λy.S(Ky))I)) = λx.(S(K(S(Kx)))
(S(λy.S(Ky))(λy.I))) = λx.(S(K(S(Kx)))(S(S(λy.S)(λy.Ky))(KI))) =
= λx.(S(K(S(Kx)))(S(S(KS)(S(KK)I))(KI))) = S(λx.(S(K(S(Kx))))(λx.[…])) =
 нет свободных вхождений х
нет свободных вхождений х
= S(S(λx.S)(λx.K(S(Kx)))(…) = S(S(KS)(S(λx.K)(λx.S(Kx)))(…) =
= (S(S(KS)(S(KK)(S(KS)(λx.Kx))))(…) = (S(S(KS)(S(KK)(S(KK)(I))(…).
Ой способ
a(bc) =(K) Kac(bc) =(S) S(Ka)bc =(K) KSa(Ka)bc =(S) S(KS)Kabc.
Базис I,B,C,S
Для всей комбинаторной логики I,B,C,S не является базисом, т.к. в нем нет укорачивающего правила, которое вводится Kxy = x. Однако для систем без укорачивающих правил I,B,C,S можно использовать как базис.
K – не может быть выражено через остальные комбинаторы, значит для всей комбинаторной логики I,B,C,S - не базис.
Преимущества комбинаторов
Не содержат свободных переменных (не возникает проблемы коллизии переменных).
Убыстряются сами вычисления, которые сводятся к ряду однотипных действий.
Контрольные вопросы
- Дайте определение комбинатора.
- Какие свойства комбинаторов делают удобным их использование для описания аппликативных алгоритмов?
- Дайте определение базиса формальной системы.
- Докажите, что I, B, C, S не является базисом бестиповой комбинаторной логики.
- Приведите определение нумералов и основных операций над ними в рамках бестиповой комбинаторной логики.
- Выразите комбинаторы B, C, W в базисе K, S.
Типизированные системы.
Использование типов.
Типы делают систему более строгой. Если все выражения согласованы по типам, то они реализуются гораздо эффективнее.
Типы назначают вид значения, когда функция прилагается к аргументам.
Предположим, что аппликация имеет тип с, В имеет тип b, тогда А имеет тип b→c.
(АВ)с-тип, Bb Ab→c
Если а,b – типы, то а→b тоже тип.
Пример.
Ix = x
Пусть Ха, тогда Ia→a (т.к. должно выполняться равенство IХа =Ха).
(Kx)y = xα
xα,yβ, то (Kx)α→β
Kxα = Cβ→α, то К α→(β→α)
Sxyz = xz(yz)
Пусть zα, тогда если (yz)β, то уα→β((хz)(уz)β)γ  (xz)β→γ, zα
(xz)β→γ, zα  xα→(β→γ)
xα→(β→γ)
Рассмотрим (Sxyz)γ, zα  (Sxy)α→γ, известно, что уα→β, тогда (Sx)(α→β)→(α→γ)
(Sxy)α→γ, известно, что уα→β, тогда (Sx)(α→β)→(α→γ)
xα→(β→γ), тогда S(α→(β→γ))→((α→β)→(α→γ))
Определение:
Говорят, что тип α приписан комбинатору Х тогда и только тогда, когда это утверждение вытекает из следующих аксиом и правила вывода:
Iα→α
Кα→(β→α)
S (α→(β→γ)) →((α→β)→(α→γ))
Xα→β, Yα
____________________
(XY) β
Обозначения:
Хα или ├#(Х) = α,
├# I = α→ α1.
Пример.
1) Припишем тип аппликации (KI)
Имеем: К α→(β→α) и Iα1→α1. Тогда существует аппликация (KI)β→α, α: α1 → α1.
Тогда (KI) β→(α1→α1)
2) (KI) β→(α→α)bβ→I γ=α→α
JScript
function foo(x) {
if (x==null) // если список пуст,
then new Array[x,3] //то результат- пара х,3
else 4 //,иначе 4
}
Расширенное λ - исчисление.
(λх(if x(@
(@ cons x).
(quote 3))
(quote 4))
cons ab →(a,b)
head (cons ab) →a
tail (cons ab) →b
Редукция графа
Любая программа может быть представлена ее синтаксическим деревом разбора.
Так как в “чистом” λ-исчислении всего две операции: λ и @, то будем в дальнейшем их использовать.
Пример. (λх.+х3)4
1-ый способ 2-ой способ
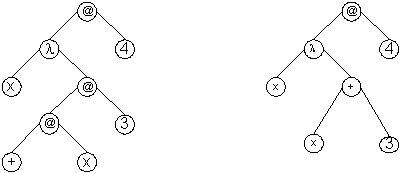
Здесь меняем все свободные вхождения х на 4
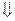
В качестве примера свернем это дерево разбора
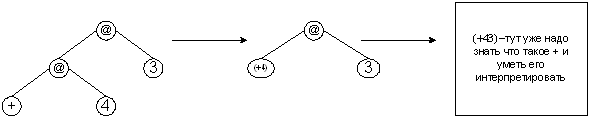
Определение:
Аппликативный порядок редукции - такой порядок редукции, который предписывает свертывать самый левый из самых внутренних редексов.
Определение:
Нормальный порядок редукции - порядок редукции, который предписывает
свертывать самый левый из самых внешних редексов.
Пример. А: λх. If x≠ 0 then x else 3/Ø. Вычислим А от 4
(Это откровенная ошибка)

При аппликативном порядке редукции мы
получим ошибку.
При аппликативном порядке вычисляются
все аргументы функции, а уже затем – сама функция.
При нормальном порядке редукции аргументы
вычисляются по мере надобности.
При редуцировании графа мы будем пользоваться
нормальным порядком редукции.
Алгоритм редукции графа (РГ)
Редукция графа будет осуществляться циклически.
Повторить:
Спускаемся по левой ветви графа до первой вершины, которая не является аппликацией, т.е. не помечена символом @.
Если эта вершина является корнем графа, то все выражение, находится в нормальной форме, значит окончание вычислений. Если она не является корнем, то она должна являться примитивной функцией либо аппликацией и у нее должны быть все необходимые аргументы (в противном случае ошибка). Мы рекурсивно применяем алгоритм для всех поддеревьев, являющихся аргументами.
Если текущая вершина является λ- вершиной, то рассматриваем следующие варианты:
1. она является корнем графа, значит выражение в нормальной форме.
2. если она не является корнем, то над ней может быть только аппликация @ и мы на место формального параметра λ-абстракции подставляем второе выражение из правой ветви аппликации. При необходимости это поддерево копируется.
Пример. (λх.+хх)7
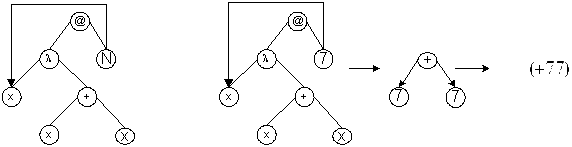
(λху.+ху)3((λх.х)4)

Суперкомбинаторы.
Определение:
Суперкомбинатором А арности n называется λ-выражение вида:
λх1…хn.Е, где на Е наложены следующие ограничения:
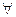 λ-абстракция в Е является суперкомбинатором, Е не является λ-абстракцией,
λ-абстракция в Е является суперкомбинатором, Е не является λ-абстракцией,
А не содержит свободных переменных, при этом n≥0 (например, 3 (const) - это суперкомбинатор, арность n = 0).
Пример:
3 - суперкомбинатор арности 0, Е=3
λху.+ху – суперкомбинатор арности 2
λх.+((λу.у)3)х n=1
λх.+(λу.+ху)3 не является суперкомбинатором, т.к. есть внутренняя λ-абстракция, которая содержит свободную переменную.
Вычислитель возьмет программу и начнет строить правила получения результата в виде супкркомбинаторов, далее будет он применять эти правила к аргументу.
Название суперкомбинаторов принято начинать со знака $.
λху.+ху
$Аab = +ab
Если этот суперкомбинатор применить к числам, то получается $A23, что также является суперкомбинатором.
$ Prog - самый верхний суперкомбинатор, позволяющий вычислить функцию.
Так как известно, что у суперкомбинаторов фиксированная арность, то вычислить, например, $A2 невозможно - не хватает аргументов.
┌──↓$B
λху.+ху=(λzу.+zу)x λх.+((λzу.+zy)x)3 теперь мы получили суперкомби-
↑───┘ └──$Bx──┘
натор (все λ-абстракции, которые выражение содержит, являются суперкомбинаторами).
Переходы такого вида называются введением экстра-параметра.
Алгоритм приведения λ-выражения к суперкомбинаторному виду
До тех пор пока в λ-выражении есть λ-абстракция. (Цикл While).
1.Выбирать λ-абстракцию, не содержащую других λ-абстракций (т.е. внутреннюю).
а) она является суперкомбинатором. Припишем ей некоторое имя и заменим ее вхождение этим именем.
б) не является суперкомбинатором, значит, содержит свободные переменные. Вынесем все свободные переменные в качестве экстра-параметров. Припишем получившейся λ-абстракции некоторое имя и заменим ее вхождение этим именем с соответствующими экстра-параметрами.
Пример.
λх.+((λу.+ху)3)х)4 = (λх.+((λz.λy +zy)x3)x)4 = { λz.λy.+zy=$A; $Aab=+ab} =
= (λх.+($Ax3)x)4 = {$Ba = +($Aa3)a} = $B4 = {$Prog=$B4} = $Prog
По λ-выражению получили набор суперкомбинаторов, по которому можем посчитать это выражение.
Определение.
Пусть $А - суперкомбинатор арности n, тогда его аппликация к n аргументам называется комбинаторным редексом.
Определение.
Суперкомбинатор арности 0 называется константной аппликативной формой.
Суперкомбинаторный редекс можно сворачивать, только если имеются все аргументы.
Пример. λху.-yх = λх.(λy-ух) = λх.+((λz.λy.-yz)x) = λх.$Yx = $X = $Y
$Yxy = -yx Устранение избыточных параметров.
$Xx = $Yx - эта строчка избыточная; по правилу (η) имеем:
$X = $Y (η)- редукция (λх.Fx=F(x 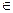 F))
F))
Упорядочивание параметров.
Пусть имеется некоторое λ-выражение:
(…(λxz.+y(*xz))…)
Выносим у как экстра-параметр:
1-ый способ: ↓подставляем у
λxz.+y(*xz) = λx.((λx.λу.λz.+y(*xz))xy) = λx.$Sxy = (λy.λx.$Sxy)y = $Ty
┌─────┐ Самая внутренняя λ-абстракция.
λx.[λz.+(*xz)].
Обозначим $Sxyz = +y(*xz) (1)
λx.$Sxy - это не суперкомбинатор.
$Tyx = $Sxy (2)
$Ty - вычисляемое выражение.
2-ой способ:
λxz.+y(*xz) = (λy.λxz.+y(*xz)))y = λx.$yx = $Ty
$Syxz = +y(*xz)
Необходимо упорядочивать свободные переменные $Tyx = $Syx так, чтобы уже связанные переменные стояли последними в списке параметров.
$T = λy



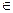 А) или х входит связанно в А.
А) или х входит связанно в А.
 Пример. х+((λх.х)3)
Пример. х+((λх.х)3)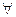 термов М и N и
термов М и N и 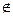 N (или х
N (или х  λу.((λу.y)7+x+y)3)
λу.((λу.y)7+x+y)3) ↑
↑ | ↓
| ↓ →(λz.+1(-2z))3→+1(-23)
→(λz.+1(-2z))3→+1(-23) ↑
↑  не сможет дать какую-либо характеристику переменной.
не сможет дать какую-либо характеристику переменной.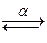 (у+(λx.-х3)2) получим свободное вхождение у и связное вхождение х.
(у+(λx.-х3)2) получим свободное вхождение у и связное вхождение х. Y -результат замены части Х вида (λх.M)N на [N/x]M:
Y -результат замены части Х вида (λх.M)N на [N/x]M: а: у→а и z→а (у
а: у→а и z→а (у 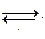 b)
b) 
 FV(F)) и при этом FX1…Xn=M соответственно F=λx1…xn.M.
FV(F)) и при этом FX1…Xn=M соответственно F=λx1…xn.M. λxy.x (так обозначим)
λxy.x (так обозначим) ½ ↓
½ ↓ └a┘└──b───┘c x z└──y──┘ z
└a┘└──b───┘c x z└──y──┘ z 




 (λху.y)AB = B
(λху.y)AB = B


 2) Список:
2) Список: 
 Голова
Голова 
 cons(x.y)→(x.y) (точечная пара)
cons(x.y)→(x.y) (точечная пара) tail(x.y) → y (хвост)
tail(x.y) → y (хвост) 
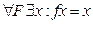
 -позволяет определить неподвижную точку.
-позволяет определить неподвижную точку.
 ↑
↑ 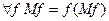 , т.е. Мƒ - неподвижная точка.
, т.е. Мƒ - неподвижная точка.
 нет свободных вхождений х
нет свободных вхождений х