|
9
| , ' 7 (
| 9
|
| B +
+
|
+
|
@ 5
| B
+
+
|
+
|
@ 5
|
| ? * >
|
| 20–25
| 16
| 18
| 10
| 12
| 14
| 8
|
| 30–35
| 18
| 20
| 12
| 14
| 16
| 10
|
| 40–45
| 20
| 22
| 14
| 16
| 18
| 12
|
| 50–55
| 22
| 24
| 16
| 18
| 20
| 14
|
| 60–65
| 24
| 26
| 18
| 20
| 22
| 16
|
| 70–80
| 26
| 28
| 20
| 22
| 24
| 18
|
| @ * >
|
| 20–25
| 18
| 22
| 12
| 14
| 16
| 10
|
| 30–35
| 20
| 24
| 14
| 16
| 18
| 12
|
| 40–45
| 22
| 26
| 16
| 18
| 20
| 14
|
| 50–55
| 24
| 28
| 18
| 20
| 22
| 16
|
| 60–65
| 26
| 30
| 20
| 22
| 24
| 18
|
| 70–80
| 28
| 32
| 22
| 24
| 26
| 20
|



 Примечание. Значение удельного расхода ВВ следует уточнять опытным путем.
Примечание. Значение удельного расхода ВВ следует уточнять опытным путем.
При корчевке пней диаметром более 1 м и при на личии мощных стержневых корней заряды располага ют в двух подкопках, выбуренных с противоположных сторон пня. Такие заряды следует взрывать одновре менно детонирующим шнуром или электродетонатора ми. Взрывание может производиться при одной под копке, но с предварительным простреливанием. При корчевке пней, расположенных на косогоре, заряд (под копа) должен располагаться с нагорной стороны.
При корчевке пней вблизи зданий и сооружений под копку ведут со стороны зданий. Величина заряда в этом случае должна быть уменьшена на 1/3 против расчетной.
#!


Таблица 7.3.

 Расчетная масса заряда ВВ (кг/пень)
Расчетная масса заряда ВВ (кг/пень)
|
&
|
9
| &
| ?
| @
| |
| ,
| 9
| ,
| 9
| |
|
| 20–29
| 30
| 0,36
| 0,28
| 0,45
| 0,32
| |
|
| 30–39
| 45
| 0,6
| 0,48
| 0,7
| 0,48
| |
| 40–49
| 60
| 0,9
| 0,7
| 1
| 0,8
| |
|
| |
| 50–59
| 75
| 1,2
| 1
| 1,4
| 1,1
| |
|
| |
| 60–69
| 90
| 1,5
| 1,3
| 1,8
| 1,4
| |
|
| 70–80
| 110
| 2
| 1,7
| 2,3
| 1,8
| |
|
| 20–29
| 30
| 0,32
| 0,24
| 0,36
| 0,28
| |
| B
| 30–39
| 45
| 0,54
| 0,42
| 0,6
| 0,45
| |
| 40–49
| 60
| 0,8
| 0,64
| 0,9
| 0,7
| |
|
| |
| 50–59
| 75
| 1
| 0,9
| 1,2
| 1
| |
| +
| |
| 60–69
| 90
| 1,3
| 1,2
| 1,5
| 1,3
| |
|
| 70–80
| 110
| 1,8
| 1,6
| 2
| 1,7
| |
|
@ 5
| 20–29
| 30
| 0,2
| 0,16
| 0,24
| 0,2
| |
| 30–39
| 45
| 0,36
| 0,3
| 0,42
| 0,36
| |
| 40–49
| 60
| 0,55
| 0,48
| 0,6
| 0,56
| |
| 50–59
| 75
| 0,8
| 0,7
| 0,9
| 0,8
| |
| 60–69
| 90
| 1,1
| 1
| 1,2
| 1,1
| |
| 70–80
| 110
| 1,4
| 1,3
| 1,6
| 1,4
| |
Если пни расположены близко один к другому и корни их тесно переплетаются, все заряды под пнями взрывают одновременно.
При размещении зарядов в шпурах, пробуренных не посредственно в древесине пней, величину зарядов опреде ляют из расчета 7,5–10 г аммонита на 1 см диаметра пня. Шпуры высверливают по оси пня вертикально или наклонно. В том и другом случаях дно шпура должно совпадать с осью пня, а глубина шпура должна быть
равна двум диаметрам пня.
Взрывные работы с целью тушения пожаров про изводятся в случаях, когда обычные средства пожаро тушения называются неэффективными. Обычно это имеет место при тушении лесных пожаров.
Для создания заградительных полос при локализа ции лесных пожаров используются специальные шлан говые заряды аммонита ПЖВ–20 диаметром 36–38 мм и длиной 10 м в бухтах, уложенных в мешки. Распола гаются такие заряды на поверхности земли. Время нахождения шланговых зарядов в воде не более 1 часа.

Механическим колебанием называют периодичес ки повторяющееся движение материальной точки (тела) по какой либо траектории, которую эта точка проходит поочередно в противоположных направ лениях. Для возникновения колебаний необходимы условия:
1. Наличие у материальной точки (тела) избыточ ной энергии (кинетической или потенциальной) по сравнению с ее энергией в положении устойчивого равновесия.
2. Действие на материальную точку (тело) возвра щающей силы.
3. Избыточная энергия, полученная материальной точкой (телом) при смещении из положения устойчи вого равновесия, не должна полностью расходоваться на преодоление сопротивления при возвращении в это положение.
Колебания, которые совершает материальная точ ка (тело) под действием только одной возвращающей силы, называются
собственными колебаниями точки (тела).
Колебания материальной точки (тела), которые происходят при действии на нее (тело) возвращающей силы и силы сопротивления среды, называются сво бодными колебаниями.

Колебания тела, которые создаются периодически действующей на тело внешней силой, называются вынужденными колебаниями. Выраженное в секундах время, затраченное на одно полное колебание, называ ется периодом колебания. Число полных колебаний тела в секунду называется частотой колебаний. Пе риод Т и частота колебаний f находятся в зависимости:
 =
=
Величина максимального отклонения колеблющей ся точки (тела) от положения ее (его) устойчивого рав новесия называется
амплитудой колебания.
Избыточная энергия колеблющейся материальной точки (тела) прямо пропорциональна ее массе, квадра ту амплитуды и квадрату частоты колебаний.
Колебания, при которых смещение подчиняется синусоидальному закону, называются гармонически ми. В частности, колебания, которые происходят под действием только одной возвращающей силы, пропор циональной смещению, являются гармоническими.
Когда возвращающей силой является равнодей ствующая силы упругости и силы тяжести, параметры колебательного движения можно связать с параметра ми движения точки по окружности.
Если точка совершает колебания с постоянными амплитудой
А и периодом
Т, то проекция на один из диаметров точки, равномерно движущейся по окружно сти с радиусом
А и периодом
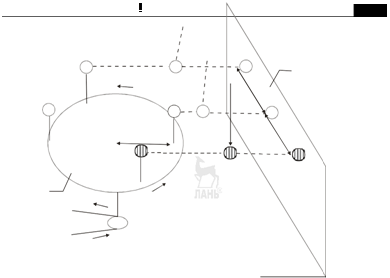
Т, совершает точно такое же колебание (рис. 1.1). Это дает возможность изучать особенности колебаний с помощью движения проекции указанной выше точки по диаметру окружности (рис. 1.2). Пусть точка
С на рис. 1.2 равномерно движется по
окружности радиуса О ’С = А, с угловой скоростью w и
совершает полный оборот за время Т. Тогда проекция точки С на прямую MN будет совершать колебания с амплитудой А и периодом Т. Если отсчет времени вести от момента, когда подвижной радиус занимает поло жение О ’С, а колеблющаяся точка — положение 0 П, то
за время t радиус повернется на угол j = w , а проек
ция его конца С переместится по прямой MN на рассто яние Х = DС 1 = 0 ПВ 1. Смещение колеблющейся точки В от положения равновесия из треугольника О ’С 1D:

Рис. 1.1. Движение проекции точки, равномерно перемещающейся по окружности, такое же как
колебание маятника:
1 — равномерно вращающийся диск; 2 — экран; Ш1, Ш1... Ш4 — положение шарика на вращающемся диске;
М1, М2, М3 — положение маятника;
Т1, Т2, Т3 — положение проекции шарика и маятника на экране.
j w
Здесьj называется фазовым углом, или
фазой, и выражается в радианах. Величинаw называется
круговой, или
циклической частотой. Отсчет времени можно
вести от любого момента, например от начальной фазы
j 0. Тогда фазу колебания можно выразить формулами:
j = j
+ w = j
+ p = j
+ p
Общее уравнение гармонического колебания примет вид:
æ p ö
(j + w ) = çèj + ÷ø = (j + p )
"

Частота колебаний
= w
p

x e A K
0 D t
N
Рис. 1.2. Связь между движением точки по окружности и движением ее проекции по диаметру. (Справа дан
график гармонического колебания).
На рис. 1.3 приведена упругая вибрационная сис тема. Пружина представляет модель таких тел, как: бал ка, колонна, упругое основание под фундаментом или упругий массив.
На рис. 1.3 (а) показаны силы, действующие на массу в момент отклонения ее от положения равнове сия. Сила тяжести
F направлена вниз, а реакция пру жины
F + КZ направлена вверх. Эта реакция включа ет реакцию пружины в положении равновесия и до полнительную реакцию, соответствующую отклонению массы от положения равновесия на величину
Z. Силы трения не учитываются. Коэффициент
К представляет жесткость пружины, имеющую размерность
Н/м.
По определению:
#
где m — масса тела;
— ускорение силы тяжести.


где
Рис. 1.3. Свободные колебания упругой системы:
а — схема действующих сил; б — траектория движения;
в — график расстояния от точки равновесия как функция времени;
г — график изменения скорости со временем; д — график изменения ускорения со временем.
По второму закону Ньютона:
 -
-
Следовательно:
—
- =
Получаем дифференциальное уравнение относи тельно Z:

 + =
+ =
Начальное условие: Z =Z 0, при t = 0 (рис. 1.3 (б)). Решение уравнения ищем в виде:
где l — постоянная;
t — время.
l
$

Подставив Z в уравнение (4), получим:
 l l + l =
l l + l =
Сокращая на l получаем характеристическое уравнение:
 l + =
l + =
Это уравнение второй степени определяет значения
l , при которых Z = l является решением уравнения (4).
Получаем:
Корни уравнения:
l
l = -
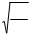
= ±
Из общих формул теории функций комплексного переменного:
или
Поэтому:
l = l + l
= l + l

 = + !
= + !
Начальное условие означает Z = Z 0 в момент вре мени t = 0.
Отсюда:
Следовательно:
 = = w " #
= = w " #

%
где w — круговая частота.

Дифференцируя Z по времени t, получим выраже ния для скорости V и ускорения a в виде:



= = - "
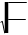 æ ö
æ ö

 = = - ç
= = - ç
÷
è ø

На рис. 1.3 (в) показан график смещения тела
Z во времени, представляющий гармоническое колебатель ное движение. На рис. 1.3 (г) показано изменение ско рости движения тела
V во времени
t. Этот график сме щен влево на p по отношению к графику 3 (в).
 На рис. 1.3 (д) показан график изменения ускоре ния тела a во времени. Этот график смещен влево на p по отношению к графику на рис. 1.3 (г).
На рис. 1.3 (д) показан график изменения ускоре ния тела a во времени. Этот график смещен влево на p по отношению к графику на рис. 1.3 (г).
Из рис. 1.3 (в) при t = T, Z = Z 0
Из выражения (9):
 = = p "
= = p "
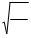 = p
= p
Откуда находим период колебаний:
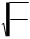 = p
= p 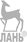
 Частоту собственных колебаний системы выразим как:
Частоту собственных колебаний системы выразим как:

=
=
Пример 1. Груз массой 5 кг кладется на пружину с жесткостью 3000 Н/м и система приходит в колеба тельное движение.
Определить: 1. Частоту и период Т собственных колебаний системы. 2. Скорости и ускорения для вре мени Т/4, Т/2, ЗТ/4 и Т.
Начальные условия: а) начало координат соответ ствует точке помещения груза на пружину; б) отсчет
&

времени ведется с момента помещения груза на пру жину.
Решение. 1. Расчетная схема приведена на рис. 1.3.
2. Дифференциальное уравнение движения:
его решение:
 +
+
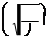 =
=
=
 = w
= w
3. 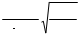
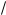 Частота собственных колебаний:
Частота собственных колебаний:
=
w = = =

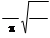

p
= !
4. Период собственных колебаний:
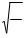
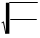 p
p
= = = p = ×


= "
w
5. 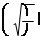 Скорость колебаний:
Скорость колебаний:

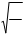
= = -
Из условия равновесия:
= " =
Следовательно:


æ ö
= -
= -
ç ÷
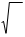
 è ø
è ø
Для моментов времени t 1 = Т/4, t 2 = Т/2, t 3 = ЗТ/4 и
 t 4 = Т
t 4 = Т скорости движения груза составят соответственно:
"'
= -
· =



|
| æ
ç
|
| ö
÷ = -
| æ p
ç
|
|
| ö
÷ = -
|
| |
| è
|
| ø
| è
|
|
| ø
|
|
| |
= - #! "

 = -
= -
= -



 p
p
p = "
 = -
= -
= -
=
= #! "
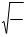 = - p =
= - p =
6. Ускорение колебаний:
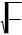
 æ ö
æ ö

 = = - ç ÷ = -
= = - ç ÷ = -
è ø
Для t 1= Т/4, t 2 = Т/2, t 3 = 3Т/4 и t 4 = Т получим соответственно:
 æ
æ
= - ç
è
ö p
 ÷ = -
÷ = -
ø
p
= "
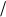 = - p = = #! "
= - p = = #! "
 = -
= -
= "
= - p = - = - #!
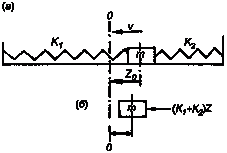
 Пример 2. Груз массой 0,5 кг расположен на глад кой горизонтальной поверхности между пружинами с жесткостью 300 и 200 Н/м. Груз смещается на рассто яние 0,15 м от положения равновесия и отпускается.
Пример 2. Груз массой 0,5 кг расположен на глад кой горизонтальной поверхности между пружинами с жесткостью 300 и 200 Н/м. Груз смещается на рассто яние 0,15 м от положения равновесия и отпускается.
Определить: 1. Период колебаний системы.
2. Наибольшую скорость и ускорение груза.
3.
Скорость и ускорение груза в момент его нахож дения на расстоянии 0,1 м от положения равновесия.
Решение. 1. Расчетная схема приведена на рис. 1.4.
2. Уравнение движения:
$% $ & $ % '('
 "
"
$ $ &$ &)*+
3. Решение дифференциального уравнения ищем в виде:
%, l
"

Рис. 1.4. Расчетная схема:
а — траектория движения; б — схема действующих сил.
Дифференцированием находим:
= l l "
 = l l
= l l
или
Тогда уравнение движения представится в виде:
l = l l
l
или
Откуда:
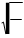

l = " =


= l + l = +
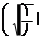
 С учетом начальных условий при t = 0; C 1 = Z 0; C 2 = 0
С учетом начальных условий при t = 0; C 1 = Z 0; C 2 = 0
"
=
= w " w =

4. Период колебаний:
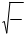
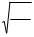 p
p
 = w = p
= w = p
= ×
= !
5.  Скорость движения массы:
Скорость движения массы:


= = -
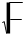


Наибольшая скорость движения массы:
'(- = -
= -
= - #!
6. Ускорение движения массы:
 æ ö
æ ö

 = = - ç ÷
= = - ç ÷
è ø
Наибольшее ускорение движения массы:


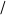 $ '(- = - = - = - #!
$ '(- = - = - = - #!
7.
Скорость движения массы в момент ее нахож дения на расстоянии
Z = 0,1 м от положения равнове сия определяем из выражения:
Откуда:
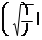
æ
ç
* "
 ö
ö

÷ - =
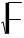

Следовательно:
= = -
= - ×
= - #!
 "
"

8. Ускорение движения массы в момент ее нахож дения на расстоянии Z = 0, 1 м от положения равно весия:
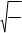 æ ö
æ ö
 = -
= -
ç ÷ = - × × = - #!


=
è ø

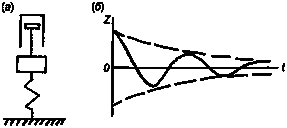
На рис. 5 (а) к массе на пружине прикреплен амортизатор. В данном случае мы имеем колебатель ную систему с демпфером.
Демпфирующая сила при нимается пропорциональной скорости движения, амортизатор представлен в виде поршня с отверстия ми в цилиндре с жидкостью.


 По аналогии с рис. 1.3 (а), уравнение движения для рис. 1.5 (а) имеет вид:
По аналогии с рис. 1.3 (а), уравнение движения для рис. 1.5 (а) имеет вид:
или
- - = = ×

 + + =
+ + =
где С — постоянная демпфирования.
Уравнение (14) представляет собой линейное од нородное дифференциальной уравнение второго по рядка с постоянными коэффициентами.
"
Рис. 1.5. Свободные колебания упруго7вязкой системы:
а — модельное представление; б — график колебаний.

Его частные решения также могут быть найдены в виде:
= l
где l — постоянная.
 Подставив частное решение в (14) и сократив на множитель l , получаем характеристическое уравне ние:
Подставив частное решение в (14) и сократив на множитель l , получаем характеристическое уравне ние:
l + l + =
Это уравнение второй степени определяет значе ния l , при которых = l является решением исход ного уравнения (14).
Если корни l 1 и l 2 уравнения (15) различны, то тем
самым найдены два независимых решения l
и l
уравнения (14). Их комбинация =
l +
l, (где
С 1 и
С 2 — произвольные постоянные), является общим ре шением уравнения (14).
Решив уравнение (15) получаем:
l =
= - ± %


Анализ полученного выражения показывает, что l могут быть как действительными, так и комп
лексными числами. Так как коэффициенты уравнения
(14) — действительные числа, то комплексные корни уравнения (15) могут быть лишь сопряженными, т. е. например: l = a + b и l = a - b.
Корни уравнения (15) будут комплексными, если
% & '
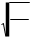
Отсюда:
>
В этом случае:
l = - + % " l = - - %
""

Применив формулы теории функций комплексно го переменного, получаем:
l = (% + %)"

Эти комплексные решения могут быть заменены действительным решением, а именно:
- -
= % + %

Поскольку показатель степени - <, то выра
жение (16) представляет собой колебания, затухающие
во времени.
В том случае, если
% & ³
то корни уравнения (14) будут действительными:
l = - ± %
и решение уравнения (14) примет вид:
=% -%


- -
.
Так как:
% =
 <
<
то решение (17) представляет собой сумму двух зату хающих экспонент и колебаний в системе не будет, то есть система, выведенная из состояния равновесия, снова возвратится в это состояние по экспоненциаль ному закону.
В частном случае если D = 0, то
 l = l
l = l
= -
"#

Отсюда:
= (

+ - !
то есть решение представляет собой одну экспоненту.
Таким образом, критерием наличия или отсутствия в системе с демпфером колебаний является величина постоянной демпфирования C.
Ес






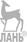




 Расчетная масса заряда ВВ (кг/пень)
Расчетная масса заряда ВВ (кг/пень)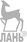

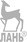

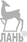




 =
= 








 -
-
 + =
+ = 
 l l + l =
l l + l =  l + =
l + = 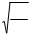
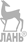

 = + !
= + !  = = w " #
= = w " #



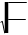 æ ö
æ ö = = - ç
= = - ç 
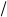 На рис. 1.3 (д) показан график изменения ускоре ния тела a во времени. Этот график смещен влево на p по отношению к графику на рис. 1.3 (г).
На рис. 1.3 (д) показан график изменения ускоре ния тела a во времени. Этот график смещен влево на p по отношению к графику на рис. 1.3 (г). = = p "
= = p "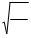 = p
= p 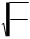 = p
= p 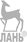
 Частоту собственных колебаний системы выразим как:
Частоту собственных колебаний системы выразим как:
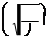 =
=  = w
= w 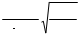
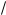 Частота собственных колебаний:
Частота собственных колебаний: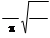

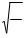
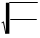 p
p
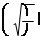 Скорость колебаний:
Скорость колебаний:
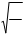



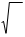
 è ø
è ø

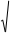 t 4 = Т скорости движения груза составят соответственно:
t 4 = Т скорости движения груза составят соответственно:




 = -
= -


 p
p = -
= -
 = - p =
= - p = 
 æ ö
æ ö = = - ç ÷ = -
= = - ç ÷ = -  æ
æ  = - p = = #! "
= - p = = #! " Пример 2. Груз массой 0,5 кг расположен на глад кой горизонтальной поверхности между пружинами с жесткостью 300 и 200 Н/м. Груз смещается на рассто яние 0,15 м от положения равновесия и отпускается.
Пример 2. Груз массой 0,5 кг расположен на глад кой горизонтальной поверхности между пружинами с жесткостью 300 и 200 Н/м. Груз смещается на рассто яние 0,15 м от положения равновесия и отпускается. "
"
 = l l
= l l 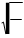



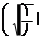
 С учетом начальных условий при t = 0; C 1 = Z 0; C 2 = 0
С учетом начальных условий при t = 0; C 1 = Z 0; C 2 = 0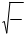
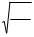 p
p = w = p
= w = p Скорость движения массы:
Скорость движения массы:
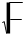


 æ ö
æ ö = = - ç ÷
= = - ç ÷ 

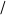 $ '(- = - = - = - #!
$ '(- = - = - = - #! 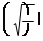
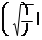
 ö
ö 

 "
" æ ö
æ ö = -
= -


 По аналогии с рис. 1.3 (а), уравнение движения для рис. 1.5 (а) имеет вид:
По аналогии с рис. 1.3 (а), уравнение движения для рис. 1.5 (а) имеет вид: + + =
+ + = 
 Подставив частное решение в (14) и сократив на множитель l , получаем характеристическое уравне ние:
Подставив частное решение в (14) и сократив на множитель l , получаем характеристическое уравне ние:




 <
< 
 l = l
l = l


