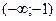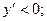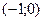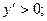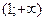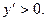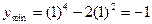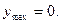Пусть функция f(x) определена в точке  и в некоторой окрестности этой точки. При каждом значении аргумента x из этого промежутка функция f(x) имеет определенное значение. Пусть аргумент
и в некоторой окрестности этой точки. При каждом значении аргумента x из этого промежутка функция f(x) имеет определенное значение. Пусть аргумент 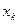 получил некоторое (положительное или отрицательное) приращение
получил некоторое (положительное или отрицательное) приращение  тогда функция y=f(x) получит некоторое приращение
тогда функция y=f(x) получит некоторое приращение  . Таким образом, при значении аргумента x будем иметь y=f(x), при значении аргумента
. Таким образом, при значении аргумента x будем иметь y=f(x), при значении аргумента 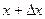 будем иметь
будем иметь 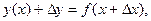 отсюда получим
отсюда получим 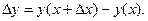 Если существует предел отношения приращения функции
Если существует предел отношения приращения функции  к приращению аргумента
к приращению аргумента 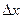 при
при  то говорят, что функция y=f(x) дифференцируема в точке x, а этот предел называют значением производной в функции y=f(x) в точке x и обозначают
то говорят, что функция y=f(x) дифференцируема в точке x, а этот предел называют значением производной в функции y=f(x) в точке x и обозначают 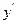
Определение. Производной данной функции y=f(x) по аргументу x называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента 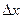 , при стремлении последнего к нулю.
, при стремлении последнего к нулю.
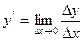 или
или 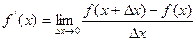
Наряду с обозначением 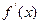 и
и 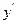 для производной употребляются и другие обозначения
для производной употребляются и другие обозначения  и
и 
Конкретное значение производной при x=a обозначается 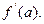
Геометрически производная представляет собой угловой коэффициент касательной к графику функции y=f(x) в точке x, т.е. к = 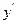 = tg
= tg  .
.
Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Основные правила дифференцирования
Пусть С - постоянная, U=u(x),V=v(x) – функции, имеющие производные. Тогда:
1. Производная постоянной равна нулю, т.е. 
2. Постоянный множитель можно выносить за знак производной, т.е. 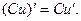
3. Производная суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций, т.е. 
4. Производная произведения находится в виде: 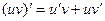 .
.
5. Производная частного находится по формуле: 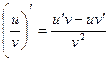 .
.
6. Производная сложной функции: если y=f(x), u=u(x), т.е. y=f(u(x)), то 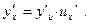
Формулы дифференцирования основных функций
1. 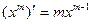 2.
2. 
3. 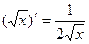 4.
4. 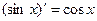
5.  6.
6. 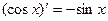
7. 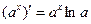 8.
8. 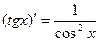
9. 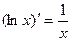 10.
10. 
11.  12.
12. 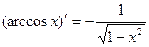
13. 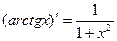 14.
14. 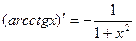
Нахождение производных
ПРИМЕР 1. y=5x
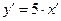
 (т.к.
(т.к. 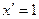 )
)
ПРИМЕР 2. 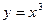

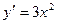
ПРИМЕР 3. 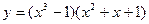
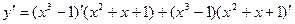
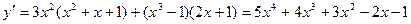
ПРИМЕР 4. 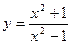

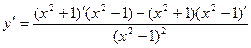

ПРИМЕР 5. 
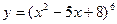
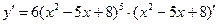
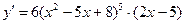
ПРИМЕР 6. 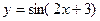

ПРИМЕР 7. 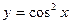
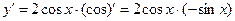
ПРИМЕР 8. 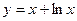
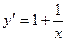
ПРИМЕР 9. 
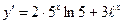
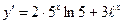
ПРИМЕР 10. 

2.4. Задачи для самостоятельного решения
1.  2.
2. 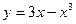
3. 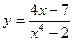 4.
4. 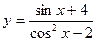
5. 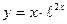 6.
6. 
7.  8.
8. 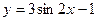
9. 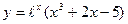 10.
10. 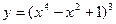
ТЕМА 3. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ
Возрастание и убывание функции
Теорема 1. Если производная функции y=f(x) положительна для всех значений x в интервале (a,в), то функция в этом интервале возрастает.
Теорема 2. Если производная функции y=f(x) отрицательна для всех значений x в интервале (а,в), то функция в этом интервале убывает.
ПРИМЕР 1 Найти интервалы возрастания и убывания функции 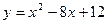
1)Найдем производную данной функции
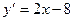
2) 2x-8<0 x<4, т.е. x изменяется в интервале 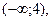 по теореме 2 в этом интервале функция убывает, т.к производная отрицательна.
по теореме 2 в этом интервале функция убывает, т.к производная отрицательна.
3) 2x-8>0 x>4, т.е. хизменяется в интервале  по теореме 1 в этом интервале функция возрастает, т.к. производная положительна.
по теореме 1 в этом интервале функция возрастает, т.к. производная положительна.
Максимум и минимум функции
Определение. Функция f(x) имеет максимум в точке  , если значение функции f(x) в точке
, если значение функции f(x) в точке  больше, чем ее значения во всех точках некоторого интервала, содержащего точку
больше, чем ее значения во всех точках некоторого интервала, содержащего точку  . Иначе говоря, функция f(x) имеет максимум при
. Иначе говоря, функция f(x) имеет максимум при  , если при всех x, достаточно близких к
, если при всех x, достаточно близких к  , выполняется неравенство
, выполняется неравенство 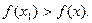
Определение. Функция f(x) в точке  имеет минимум, если значение функции f(x) в точке
имеет минимум, если значение функции f(x) в точке  меньше, чем ее значения во всех точках некоторого интервала, содержащего точку
меньше, чем ее значения во всех точках некоторого интервала, содержащего точку  . Иначе говоря, если выполняется неравенство
. Иначе говоря, если выполняется неравенство 
Максимум и минимум функции называют экстремумами. Экстремальные значения функции и их расположение на отрезке  в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
Теорема 1. (необходимое условие экстремума)
Если дифференцируемая функция y=f(x) имеет в точке  максимум (max) или минимум (min), то ее производная обращается в нуль в этой точке, т.е.
максимум (max) или минимум (min), то ее производная обращается в нуль в этой точке, т.е. 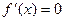 , точка
, точка  в этом случае называется критической точкой.
в этом случае называется критической точкой.
Если производная не существует в какой-либо точке, то в этой точке производная терпит разрыв.
Теорема 2. (достаточное условие существования экстремума)
Пусть функция f(x) непрерывна в некотором интервале, содержащем критическую точку  и дифференцируема во всех точках этого интервала (кроме самой точки
и дифференцируема во всех точках этого интервала (кроме самой точки  ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при
). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при  функция имеет максимум. Если же меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
функция имеет максимум. Если же меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
ПРИМЕР 2. Найти экстремумы функции 
1. Найдем производную функции 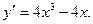
2. Определим критические точки, для этого приравняем производную к нулю. 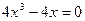



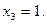
Функция определена и непрерывна на всей числовой прямой, точки 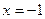 ,
,  ,
, 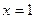 являются критическими.
являются критическими.
3. Исследуем критические точки, определяя знак производной слева и справа от каждой из них, для этого наносим точки на числовую ось и определяем знак производной внутри каждого интервала.
На интервале 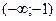
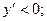
На интервале 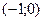
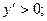
На интервале 
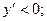
На интервале 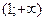
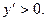
При переходе через точки 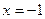 ,
, 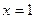 знак производной сменился с (-) на (+), Следовательно, в этих точках функция имеет минимум (min), а при переходе через точку x=0 знак производной сменился с (+) на (-), следовательно в этой точке функция имеет максимум (max).
знак производной сменился с (-) на (+), Следовательно, в этих точках функция имеет минимум (min), а при переходе через точку x=0 знак производной сменился с (+) на (-), следовательно в этой точке функция имеет максимум (max).
4. Найдем значение функции в этих точках

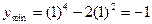
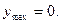



 и в некоторой окрестности этой точки. При каждом значении аргумента x из этого промежутка функция f(x) имеет определенное значение. Пусть аргумент
и в некоторой окрестности этой точки. При каждом значении аргумента x из этого промежутка функция f(x) имеет определенное значение. Пусть аргумент 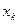 получил некоторое (положительное или отрицательное) приращение
получил некоторое (положительное или отрицательное) приращение  тогда функция y=f(x) получит некоторое приращение
тогда функция y=f(x) получит некоторое приращение  . Таким образом, при значении аргумента x будем иметь y=f(x), при значении аргумента
. Таким образом, при значении аргумента x будем иметь y=f(x), при значении аргумента 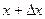 будем иметь
будем иметь 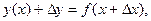 отсюда получим
отсюда получим 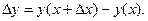 Если существует предел отношения приращения функции
Если существует предел отношения приращения функции 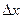 при
при  то говорят, что функция y=f(x) дифференцируема в точке x, а этот предел называют значением производной в функции y=f(x) в точке x и обозначают
то говорят, что функция y=f(x) дифференцируема в точке x, а этот предел называют значением производной в функции y=f(x) в точке x и обозначают 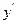
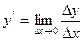 или
или 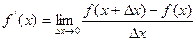
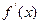 и
и  и
и 
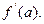
 .
.
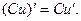

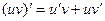 .
.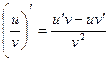 .
.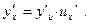
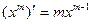 2.
2. 
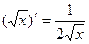 4.
4. 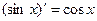
 6.
6. 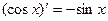
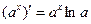 8.
8. 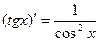
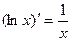 10.
10. 
 12.
12. 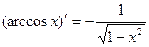
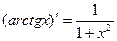 14.
14. 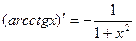
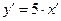
 (т.к.
(т.к. 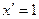 )
)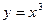

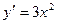
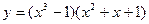
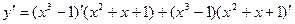
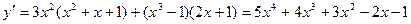
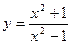

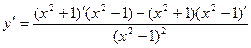

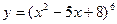
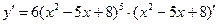
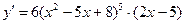

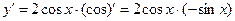
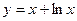
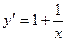

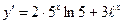


 2.
2. 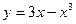
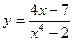 4.
4. 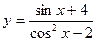
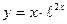 6.
6. 
 8.
8. 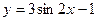
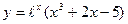 10.
10. 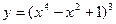
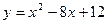
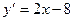
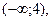 по теореме 2 в этом интервале функция убывает, т.к производная отрицательна.
по теореме 2 в этом интервале функция убывает, т.к производная отрицательна. по теореме 1 в этом интервале функция возрастает, т.к. производная положительна.
по теореме 1 в этом интервале функция возрастает, т.к. производная положительна. , если при всех x, достаточно близких к
, если при всех x, достаточно близких к 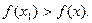

 в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
в известной степени характеризуют изменение функции в зависимости от изменения аргумента.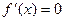 , точка
, точка 
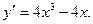
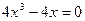



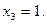
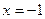 ,
,  ,
, 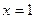 являются критическими.
являются критическими.