Задачу потребительского выбора заменим задачей на условный экстремум:
U (х1, х2) → max
при условии (4)
р1х1 + р2х = I
Для решения задачи применим метод Лагранжа.
Выписываем функцию Лагранжа:
L (х1, х2, λ) = U (х1, х2) + λ (р1х1 + р2х2 – I), (5)
находим ее первые частные производные по переменным х1, х2, λ; приравниваем эти частные производные к нулю:
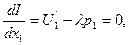
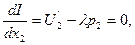
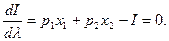
Исключив из полученной системы трех уравнений с тремя неизвестными, неизвестную λ, получим систему двух уравнений с двумя неизвестными х1 и х2
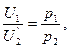
р1х1 + р2х2 = I.
Решение (х10, х20) этой системы есть «укороченная» критическая точка функции Лагранжа.
Можно строго доказать, что «укороченная» критическая точка (х19, х20) функции Лагранжа обязательно есть решение задачи потребительского выбора (за исключением так называемых угловых решений, которые не рассматриваются).
Подставив решение (х19, х20) в левую часть равенства
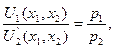 (6)
(6)
получим что в точке (х10, х20) локального рыночного равновесия индивидуума отношение предельных полезностей U1́(х10, х20) и U2́(х10, х20) продуктов равно отношению рыночных цен р1 и р2 на эти продукты:
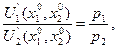
В связи с тем, что отношение 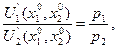 равно предельной норме за-
равно предельной норме за-
мены первого продукта вторым в точке локального рыночного равновесия (х10, х20) из (6) следует, что эта предельная норма равна отношению рыночных цен 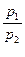 на продукты. Приведенный результат играет важную роль в экономической теории.
на продукты. Приведенный результат играет важную роль в экономической теории.
Геометрически решение (х10, х20) можно интерпретировать как точку касания линии безразличия функции полезности U(х1, х2) с бюджетной прямой р1х1 + р2х2 = I (рис.2). Это определяется тем, что отношение
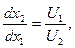 показывает тангенс угла наклона бюджетной прямой.
показывает тангенс угла наклона бюджетной прямой.
Поскольку в точке потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание двух линий.
Из приближенного равенства
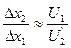 , и соотношения (6)
, и соотношения (6)
следует, что
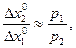 (7), т.е. отношение (со знаком минус) конечных (относительно небольших) изменений Δх20 и Δх10 объемов продуктов в локальном рыночном равновесии (х10, х20) приближенно равно отношению рыночных цен р1 и р2 на продукты.
(7), т.е. отношение (со знаком минус) конечных (относительно небольших) изменений Δх20 и Δх10 объемов продуктов в локальном рыночном равновесии (х10, х20) приближенно равно отношению рыночных цен р1 и р2 на продукты.
Выводы. Равенство (7) позволяет давать приближенные оценки отношению рыночных цен, если известны конечные изменения объемов продуктов относительно потребительского набора, приобретенного потребителем, т.е. набора, который естественно следует толковать в качестве оптимального для потребителя.
Координаты х10 и х20 решения (х10 и х20) задачи потребительского выбора есть функция параметров р1, р2, I:
х10 = х10 (р1, р2, I),
х20 = х20 (р1, р2, I).
Полученные функции называются функциями спроса на первый и второй продукты.
Важным свойством функции спроса является их однородность нулевой степени относительно цен и дохода, т.е. значения функций спроса инвариантны по отношению к пропорциональным изменениям цен и дохода.
х10 (λр1, λр2, λI) = х10 (р1, р2, I)
х20 (λр1, λр2, λI) = х20 (р1, р2, I) для любого λ > 0.
Это означает, что если цены и доход изменятся в одно и то же число раз, величина спроса на продукт (первый или второй – безразлично) остаются неизменной.
Пример задачи потребительского выбора
Пусть неизвестные количества благ равны х1 и х2, а их рыночные цены р1 и р2:
U (х1, х2) = х1 х2 → max
р1х1 + р2х2 ≤ I
х1 ≥ 0, х2 ≥ 0,
Бюджетное ограничение в оптимальной точке должно выполняться как равенство, и поскольку ода блага жизненно необходимы (полезность равна нулю, если одно из них отсутствует), требования неотрицательности переменных будут выполнены автоматически. Следовательно, решаемая задача математического программирования превращается в классическую задачу на условный экстремум. Запишем необходимые условия экстремума: отношения предельных полезностей благ должны равняться отношениям их рыночных цен, а бюджетное ограничение выполняется как равенство.
Получим систему уравнений:
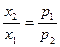
р1х1 + р2х2 = I
Первое условие означает, в задаче количество денег на оба блага, должны быть одинаковыми,
то есть х2 р2 = х1 р1.
Это вытекает из равенства «весов», или показателей степени у переменных х1 и х2 в функциях полезности.
Итак
х2 р2 = р1 х1 = 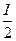
и функция спроса приобретает вид:
х1 =  ; х2 =
; х2 = 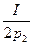 .
.
Расход на каждое благо составляет половину дохода потребителя, и чтобы найти необходимое количество каждого блага, следует разделить расходуемую на него сумму на его цену.
Самостоятельно для этой простой модели найти решение без использования метода множителей Лагранжа, выражая х2 через х1 из бюджетного ограничения, подставляя это выражение в функцию полезности (которая становится полиномом второй степени от одной переменной) и находя максимум полученной квадратичной функции.



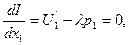
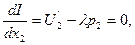
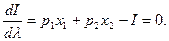
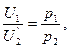
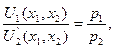 (6)
(6)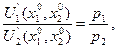
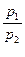 на продукты. Приведенный результат играет важную роль в экономической теории.
на продукты. Приведенный результат играет важную роль в экономической теории.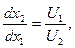 показывает тангенс угла наклона бюджетной прямой.
показывает тангенс угла наклона бюджетной прямой.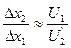 , и соотношения (6)
, и соотношения (6)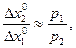 (7), т.е. отношение (со знаком минус) конечных (относительно небольших) изменений Δх20 и Δх10 объемов продуктов в локальном рыночном равновесии (х10, х20) приближенно равно отношению рыночных цен р1 и р2 на продукты.
(7), т.е. отношение (со знаком минус) конечных (относительно небольших) изменений Δх20 и Δх10 объемов продуктов в локальном рыночном равновесии (х10, х20) приближенно равно отношению рыночных цен р1 и р2 на продукты.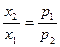
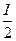
 ; х2 =
; х2 = 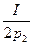 .
.


