

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
М. Ю. Ястребов
Электронное учебное пособие по дисциплине
Высшая математика
Семестр
Материал для подготовки к коллоквиуму
Матрицы, определители, системы линейных уравнений,
Векторная алгебра
Направление 38.03.04
«Государственное и муниципальное управление»
Санкт-Петербург 2020
ВВЕДЕНИЕ
Электронное учебное пособие по дисциплине «Высшая математика» предназначено для обучающихся по направлению 38.03.04 «Государственное и муниципальное управление», может быть использовано при изучении других дисциплин, направленных на формирование профессиональных компетенций. Изложенный материал соответствует той части семестрового материала, которая входит в программу коллоквиума1-го семестра.
Электронное учебное пособие направлено на формирование общепрофессиональных компетенций в соответствии с федеральным государственным образовательным стандартом (ФГОС ВО 3++) по уровню бакалавриата академического:
– ОПК-2 Способен применять соответствующий физико-математический аппарат, методы анализа и моделирования, теоретического и экспериментального исследования при решении профессиональных задач.
В электронном учебном пособии содержится систематическое изложение основ теории матриц и определителей, векторной алгебры.
Цель электронного учебного пособия – сформировать у обучающихся системные знания в области указанного раздела математики, которые позволят в будущем осуществлять профессиональную деятельность.
Содержание данного электронного учебного пособия соответствует рабочей программе дисциплины и основано на материалах отечественной и зарубежной научной и учебной литературы, включая современные публикации.
|
|
АННОТАЦИЯ ДИСЦИПЛИНЫ «ВЫСШАЯ МАТЕМАТИКА»
приложение 2

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Государственный университет морского и речного флота имени адмирала С.О. Макарова»
Кафедраматематики
АННОТАЦИЯ
Дисциплина математика
Направление подготовки 38.03.04 Государственное и муниципальное управление
Профиль Социально-экономическое развитие прибрежных территорий
Уровень высшего образования бакалавриат (академический)
Промежуточная аттестация зачет, экзамен
1. Место дисциплины в структуре образовательной программы
Дисциплина «Математика» относится к базовой части Блока 1 и изучается на 1 курсе в I-II семестрах по очной форме обучения.
Дисциплина «Математика» является одной из основных фундаментальных учебных дисциплин; она обеспечивает подготовку бакалавров к успешному освоению дисциплин гуманитарно-социально-экономического, естественнонаучно-математического и профессионального циклов.
Основная задача курса «Математика»: привить навыки решения типовых задач, научить студентов прилагать полученные теоретические знания к решению сугубо практических задач.
Входные знания студента:
· курс средней общеобразовательной школы «Алгебра и начала анализа»,
· курс средней общеобразовательной школы «Геометрия».
Данная дисциплина тесно связана со следующими дисциплинами:
- Теория вероятностей и математическая статистика;
- Статистика;
- Информационные технологии в управлении;
- Экономическая теория;
- Теория управления;
- Математическая экономика;
- Основы математического моделирования социально-экономических процессов.
2. Планируемые результаты обучения по дисциплине
|
|
В результате освоения дисциплины обучающийся должен:
Знать:основные понятия, определения и инструменты высшей математики и их применение в развитии современного общества. Знать основылинейной алгебры, аналитической геометрии, теории дифференциальных уравнений, теории вероятностей и математической статистики
Уметь: логически мыслить, проводить доказательства основных утверждений, устанавливать логические связи между понятиями, самостоятельно решать классические задачи высшей математики Уметь выполнять действия с матрицами, вычислять определители. Решать системы алгебраических уравнений. Решать дифференциальные уравнения и задачи теории вероятностей и математической статистики различными методами.
Владеть: математическим аппаратом теории матриц и определителей, дифференциального и интегрального исчисления. Владеть математическим аппаратом дифференциальных уравнений, теории вероятностей и математической статистики для решения практических задач.
3. Объем дисциплины по видам учебных занятий
Объем дисциплины составляет 5 зачетных единиц, всего 180 часов, из которых по очной/заочной формам обучения 108/20 часов составляет контактная работа обучающегося с преподавателем.
4. Основное содержание дисциплины
Понятие матрицы, определителя, свойства определителя. Теоремы разложения и аннулирования, теорема Крамера. Действия с матрицами.
Числовая последовательность, ее предел. Бесконечно малые и бесконечно большие величины, их свойства. Предел функции. Непрерывность функции. Основные пределы анализа. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые. Классификация точек разрыва функции.
Производная, ее геометрический и физический смысл. Правила дифференцирования. Производная сложной функции. Теорема Лопиталя. Свойства функции: монотонность, экстремумы, выпуклость вверх и выпуклость вниз, точки перегиба, асимптоты.
Проекция вектора на ось, ее свойства. Понятие базиса совокупности векторов. Скалярное и векторное произведения.
Прямая на плоскости. Кривые 2-го порядка. Плоскость. Прямая в пространстве.
Первообразная, неопределенный интеграл, свойства. Интегрирование по частям, замена переменной. Определенный интеграл, его геометрический смысл, свойства. Формула Ньютона-Лейбница. Несобственные интегралы. Понятие n -мерного пространства.
|
|
Функция двух переменных. Полное и частные приращения. Частные производные. Экстремум функции 2-х переменных.
Алгебраическая, тригонометрическая, показательная формы комплексного числа. Действия с комплексными числами. Функция комплексной переменной.
Понятие дифференциального уравнения, его порядок, общее и частное решения. Дифференциальные уравнения 1-го и 2-го порядка.
Перестановки, сочетания, размещения. Виды случайных событий, действия с ними. Аксиомы теории вероятностей. Теорема сложения. Условная вероятность. Теорема умножения вероятностей. Формула Бернулли
Дискретные и непрерывные случайные величины. Числовые характеристики. Основные законы распределения случайных величин.
Эмпирическая функция распределения. Полигон и гистограмма. Точечные оценки математического ожидания и дисперсии.
Составитель: Ильичева Т.П.
Зав. кафедрой: Сухотерин М.В.
ЛИНЕЙНАЯ АЛГЕБРА
1.1. Понятие матрицы
Прямоугольная таблица чисел из m строк и n столбцов называется матрицей размера 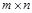 .
.
Числа, из которых состоит матрица, называются элементами матрицы.
Элементы матрицы нумеруются двумя индексами: первый указывает номер строки, содержащей этот элемент, а второй — номер столбца.
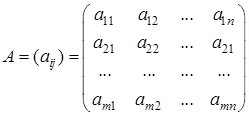
Матрицы размера 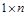 называются строками:
называются строками: 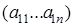 ;
;
Матрицы размера 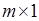 называются столбцами:
называются столбцами:  .
.
Матрица размера 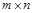 , состоящая из нулей, называется нулевой.
, состоящая из нулей, называется нулевой.
Матрицы 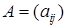 и
и 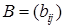 равны, если они имеют одинаковый размер и попарно равны их соответствующие элементы:
равны, если они имеют одинаковый размер и попарно равны их соответствующие элементы: 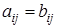
1.2. Матричные операции
Операция транспонирования переводит матрицу А размера 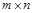 в матрицу
в матрицу 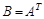 размера
размера 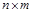 и состоит в замене строк таблицы на ее столбцы с сохранением порядка. Таким образом, в матрице
и состоит в замене строк таблицы на ее столбцы с сохранением порядка. Таким образом, в матрице 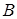 элемент
элемент 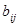 равен элементу
равен элементу 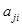 матрицы
матрицы 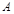 .
.
Верно равенство 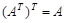 .
.
Операция сложения применима только к матрицам одинакового размера. Суммой двух матриц 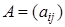 и
и  размера
размера 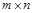 называется матрица
называется матрица 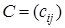 того же размера, элементы которой представлены суммой элементов матриц
того же размера, элементы которой представлены суммой элементов матриц 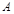 и
и 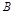 , имеющих те же индексы:
, имеющих те же индексы:
|
|
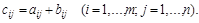
Обозначение: 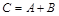 .
.
Операция вычитания определяется аналогично:
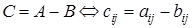 .
.
Операция умножения матрицы на число.Произведением матрицы 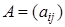 на число a называется матрица
на число a называется матрица 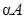 того же размера, что и
того же размера, что и 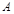 , получающаяся умножением каждого элемента матрицы
, получающаяся умножением каждого элемента матрицы 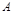 на число a:
на число a: 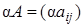 . Обозначение:
. Обозначение: 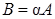 .
.
Введённые операции удовлетворяют следующим равенствам для любых матриц 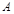 и
и 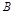 одинакового размера
одинакового размера 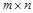 и любых чисел a, b:
и любых чисел a, b:
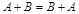 — коммутативность сложения;
— коммутативность сложения;
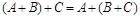 — ассоциативность сложения;
— ассоциативность сложения;
если 0 — нулевая матрица размера m ´ n, то A + 0 = A;
для матрицы 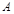 существует матрица
существует матрица 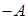 того же размера такая, что A +
того же размера такая, что A + 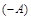 = 0; при этом
= 0; при этом 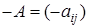 ;
;
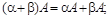
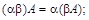
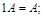
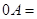 0 — нулевая матрица того же размера, что и
0 — нулевая матрица того же размера, что и 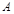 ;
;
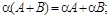
10) (А + В) Т = АТ + ВТ;
11) 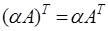 .
.
1.3. Умножение матриц
Произведение матриц вводится только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матриц 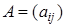 размера
размера 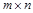 и
и 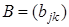 размера
размера 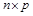 называется матрица
называется матрица 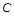 размера
размера 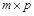 , элемент которой
, элемент которой 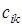 вычисляется по формуле («строка на столбец»)
вычисляется по формуле («строка на столбец»)
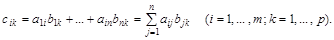
Отметим, что 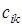 есть сумма попарных произведений элементов i -й строки матрицы
есть сумма попарных произведений элементов i -й строки матрицы 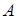 на элементы j-го столбца матрицы
на элементы j-го столбца матрицы 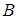 .
.
Обозначение: 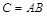 .
.
Операция умножения матриц не является в общем случае коммутативной (перестановочной), т.е. 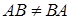 (хотя для некоторых матриц такое равенство имеет место). Более того, произведение АВ может существовать (в силу правила размерностей для множителей), в то время как произведение ВА оказывается не имеющим смысла.
(хотя для некоторых матриц такое равенство имеет место). Более того, произведение АВ может существовать (в силу правила размерностей для множителей), в то время как произведение ВА оказывается не имеющим смысла.
Операция умножения добавляет к указанным в п. 1.2 равенствам следующие соотношения:
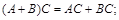
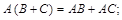
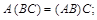
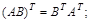
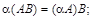
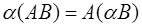 ,
,
Данные равенства надо понимать так: если определено выражение справа, то определено и выражение слева (и наоборот) и имеет место указанное равенство.
Замечание. Произведением матрицы 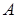 размера
размера 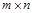 и столбца
и столбца 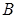 размера
размера 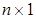 оказывается столбец
оказывается столбец 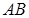 размера
размера 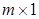
1.4. Квадратные матрицы
Матрица, в которой число строк равно числу столбцов, называется квадратной. Число строк квадратной матрицы называется порядком матрицы. Матрицы одного порядка можно складывать и вычитать, умножать на число и перемножать между собой. Элементы, стоящие в строках и столбцах с одинаковыми номерами, образуют главную диагональ. Матрица 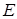 с единицами на главной диагонали и нулями на остальных местах
с единицами на главной диагонали и нулями на остальных местах
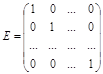
называется единичной.
Для произвольной квадратной матрицы 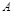 одного порядка с единичной матрицей
одного порядка с единичной матрицей 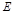 верно равенство
верно равенство
АЕ = ЕА = А.
1.5. Определители
С каждой квадратной матрицей А можно связать число, называемое определителем (или детерминантом)матрицы, который обозначается 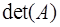 или
или 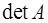 , или
, или 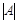 .
.
Для матрицы первого порядка её определителем считается единственный элемент матрицы: 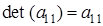 .
.
Для матрицы 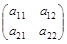 второго порядка определитель задаётся формулой
второго порядка определитель задаётся формулой
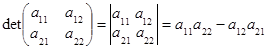 .
.
Для матрицы третьего порядка определитель задаётся формулой
|
|
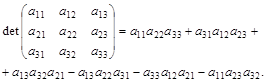

Пусть A — квадратная матрица порядка n и  — элемент, стоящий в строке с номером
— элемент, стоящий в строке с номером 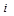 и столбце с номером
и столбце с номером 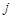 . Минором
. Минором 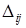 элемента
элемента 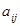 называется определитель матрицы, которая получается из
называется определитель матрицы, которая получается из 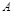 вычёркиванием строки и столбца, на пересечении которых находится элемент
вычёркиванием строки и столбца, на пересечении которых находится элемент 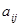 .
.
Пример. Пусть  .
.
Тогда минор 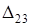 элемента
элемента 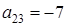 — это число
— это число 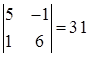 .
.
Алгебраическим дополнением элемента 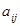 называется число
называется число 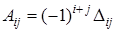 .
.
Если 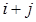 является чётным числом, то
является чётным числом, то
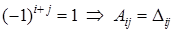 ;
;
если же 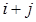 является нечётным числом, то
является нечётным числом, то
 .
.
Если в матрице 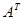 каждый элемент заменить на его алгебраическое дополнение, то получится матрица, которая называется союзной к матрице
каждый элемент заменить на его алгебраическое дополнение, то получится матрица, которая называется союзной к матрице 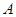 и обозначается А *.
и обозначается А *.
Теорема (о разложении определителя). Определитель матрицы равен сумме попарных произведений элементов какой-либо строки на их алгебраические дополнения:
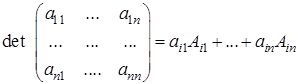 .
.
Это — разложение определителя по элементам 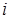 -й строки.
-й строки.
Разложение определителя по элементам 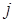 -го столбца имеет вид:
-го столбца имеет вид:
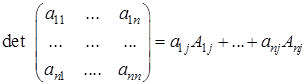
Теорема (аннулирования). Сумма произведений элементов какой-либо строки на алгебраические дополнения соответствующих элементов (стоящих в том же столбце) другой строки равна нулю.
ai 1 Aj 1 + … + ainAjn = 0 при i ¹ j.
Теорема (об определителе транспонированной матрицы). При транспонировании определитель матрицы не меняется:
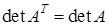 .
.
Свойства определителей
Последняя из приведённых теорем позволяет любое свойство определителей, сформулированное в терминах строк матрицы, переформулировать в терминах её столбцов.
1. Если в матрице есть строка, состоящая из нулей, то определитель такой матрицы равен нулю.
2. Если в матрице поменять местами две строки, то определитель такой матрицы будет равен произведению определителя исходной матрицы на -1.
3. Если в матрице есть две одинаковые строки, то её определитель равен нулю.
4. Если все элементы какой-нибудь строки матрицы умножить на одно и тоже число, то определитель новой матрицы будет равен произведению определителя исходной матрицы на это число.
5. Если элементы какой-нибудь строки матрицы представлены в виде суммы двух слагаемых, то определитель такой матрицы равен сумме определителей двух матриц, совпадающих с исходной, кроме упомянутой строки, а в этой строке в первой матрице стоят первые слагаемые, а во второй матрице — вторые слагаемые:
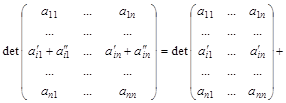
 .
.
6. Если в матрице к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, то определитель полученной матрицы будет равен определителю исходной матрицы.
7. Определитель произведения матриц равен произведению определителей этих матриц:
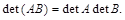
1.6. Обратная матрица
Если 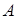 — квадратная матрица порядка
— квадратная матрица порядка 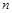 , то матрица
, то матрица 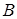 того же порядка называется обратной к матрице
того же порядка называется обратной к матрице 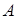 , если выполнено равенство
, если выполнено равенство
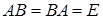 ,
,
где Е — единичная матрица.
Обозначение: 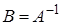 . Таким образом,
. Таким образом,
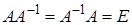
Е сли матрица В является обратной к матрице А, то матрица А является обратной к матрице В:
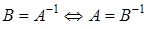 .
.
Пусть матрица А имеет обратную А -1, так что 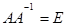 . По свойству определителей
. По свойству определителей 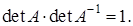 , так что
, так что 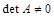 и
и 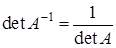 .
.
Теорема (о существовании обратной матрицы). Для того чтобы матрица 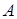 имела обратную
имела обратную 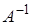 необходимо и достаточно, чтобы её определитель был отличен от нуля; при этом
необходимо и достаточно, чтобы её определитель был отличен от нуля; при этом 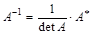 , где А * — союзная матрица.
, где А * — союзная матрица.
Алгоритм вычисления обратной матрицы:
- каждый элемент матрицы 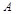 заменяется на его алгебраическое дополнение;
заменяется на его алгебраическое дополнение;
- полученная матрица транспонируется;
- полученная матрица умножается на число 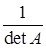 .
.
Другой способ нахождения обратной матрицы приведён в п. 1.10.
1.7. Решение систем линейных уравнений методом обратной матрицы
Рассмотрим систему линейных уравнений, в которой число неизвестных равно числу уравнений:
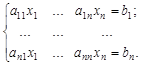 (1)
(1)
Обозначим:
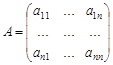 — матрица коэффициентов;
— матрица коэффициентов;
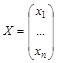 — столбец неизвестных;
— столбец неизвестных;
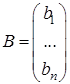 — столбец свободных членов.
— столбец свободных членов.
Тогда, используя определения матричных операций, можно систему (1) переписать как равенство одностолбцовых матриц:
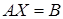 . (2)
. (2)
Равенство (2) называется матричной записью системы линейных уравнений.
Если здесь 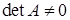 , то существует обратная матрица
, то существует обратная матрица 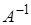 . Имеем тогда:
. Имеем тогда:
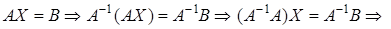

Тем самым найдено решение системы Х = A -1 В в матричном виде: 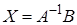 .
.
1.8. Решение систем линейных уравнений методом Крамера
Рассмотрим снова систему 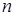 линейных уравнений с
линейных уравнений с 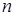 неизвестными:
неизвестными:
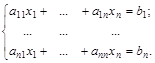
Введём обозначения:
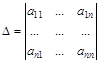 — определитель системы, составленный из коэффициентов при неизвестных,
— определитель системы, составленный из коэффициентов при неизвестных,
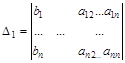 — определитель при неизвестном
— определитель при неизвестном 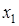 ,
,
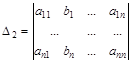 — определитель при неизвестном
— определитель при неизвестном 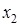 ,
,
и так далее;
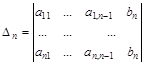 — определитель при неизвестном
— определитель при неизвестном 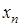 .
.
Здесь определитель 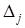 при неизвестном
при неизвестном 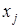 получается из определителя системы
получается из определителя системы 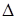 заменой
заменой 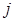 -го столбца столбцом свободных членов.
-го столбца столбцом свободных членов.
Теорема Крамера. Если определитель 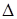 системы линейных уравнений не равен нулю, то система имеет единственное решение, которое задаётся формулами Крамера:
системы линейных уравнений не равен нулю, то система имеет единственное решение, которое задаётся формулами Крамера:
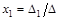 ,
, 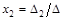 ,...,
,..., 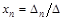 .
.
Пример.
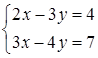 ;
;
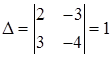 ;
; 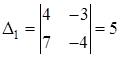 ;
; 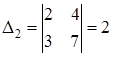 ;
;
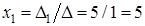 ;
; 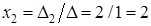 .
.
1.9. Решение систем линейных уравнений методом Гаусса
Метод Гауссарешения произвольнойсистемылинейных уравненийосновывается на идее последовательного исключения неизвестных.
Пусть дана система из m уравнений с n неизвестными
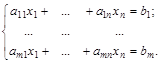
Выберем среди всех коэффициентов 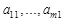 коэффициент, отличный от нуля. Переставив, в случае необходимости, строки и изменив соответствующим образом нумерацию уравнений и неизвестных (а значит, строк и столбцов матрицы), можно добиться, чтобы это был
коэффициент, отличный от нуля. Переставив, в случае необходимости, строки и изменив соответствующим образом нумерацию уравнений и неизвестных (а значит, строк и столбцов матрицы), можно добиться, чтобы это был 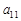 .
.
Выразив 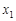 из первого уравнения системы, получим:
из первого уравнения системы, получим:
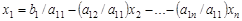 .
.
Подставив затем полученное выражение для 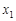 в оставшиеся уравнения, получим систему, у которой как число уравнений, так и число неизвестных уменьшилось на единицу.
в оставшиеся уравнения, получим систему, у которой как число уравнений, так и число неизвестных уменьшилось на единицу.
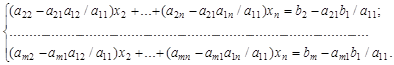
Переобозначим:  ;
; 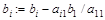 , в результате получаем систему
, в результате получаем систему
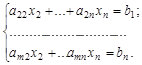
Если 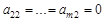 , то вычёркиваем этот столбец коэффициентов при
, то вычёркиваем этот столбец коэффициентов при  из системы, а переменную
из системы, а переменную 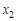 считаем произвольной. В противном случае повторим с новой системой то же, что и с исходной.
считаем произвольной. В противном случае повторим с новой системой то же, что и с исходной.
Так мы переходим от системы к системе, вычеркивая нулевые столбцы, пока не останется одно уравнение. Если на каком-то этапе у нас получится равенство 0 = bk, где bk ¹0, то система не имеет решений. В противном случае оставшееся последним уравнение будет иметь вид:
 ,
,
где 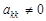 .
.
Затем находим
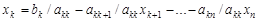 ,
,
где 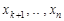 выбираются произвольно. Далее обратным ходом последовательно находятся
выбираются произвольно. Далее обратным ходом последовательно находятся 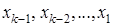
1.10. Нахождение обратной матрицы методом Гаусса
Элементарными преобразованиями матрицы произвольного размера называются следующие действия со строками:
- перестановка строк;
- прибавление ко всем элементам одной строки соответствующих элементов другой строки, умноженных на некоторое число;
- деление всех элементов строки на число, отличное от нуля.
Пусть 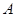 — квадратная матрица порядка
— квадратная матрица порядка 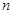 . Будем искать обратную матрицу следующим способом: запишем подряд две матрицы
. Будем искать обратную матрицу следующим способом: запишем подряд две матрицы
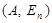 ,
,
где 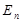 — единичная матрица порядка
— единичная матрица порядка 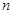 . Используя элементарные преобразования над строками приведём матрицу
. Используя элементарные преобразования над строками приведём матрицу 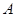 к единичной
к единичной 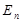 . Тогда у нас получится матрица
. Тогда у нас получится матрица 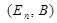 .
.
Можно доказать, что 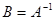 .
.
Пример. Пусть 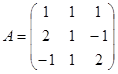 . Вычислим обратную матрицу
. Вычислим обратную матрицу 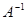 .
.
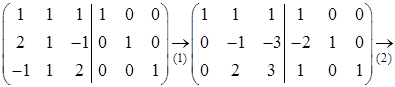
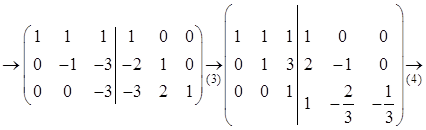
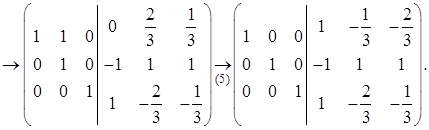
Поясним сделанные преобразования. На первом шаге ко второй строке прибавили первую, умноженную на (-2), а к третьей — первую (умноженную на единицу).
На втором шаге к третьей строке прибавили вторую, умноженную на 2.
На третьем шаге вторую строку разделили на (-1), а третью на (-3).
На четвертом шаге к первой строке прибавили третью, умноженную на (-1), а ко второй — третью, умноженную на (-3).
Наконец, на заключительном, пятом шаге к первой строке прибавили вторую, умноженную на (-1). В результате получили
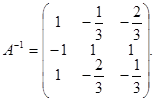
Замечание. Если в результате указанных элементарных преобразований в некоторой строке все элементы левее вертикальной черты окажутся равными нулю, то это означает, что 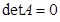 и, следовательно, обратная матрица
и, следовательно, обратная матрица 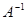 не существует.
не существует.
1.11. Собственные числа и собственные векторы
Пусть 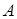 — квадратная матрица размера n ´ n,
— квадратная матрица размера n ´ n, 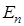 — единичная матрица того же порядка.
— единичная матрица того же порядка.
Число 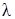 называется собственным числом матрицы A, если найдётся такой ненулевой столбец
называется собственным числом матрицы A, если найдётся такой ненулевой столбец 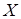 , что
, что 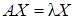 . В этом случае столбец
. В этом случае столбец 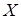 называется собственным вектором матрицы A, соответствующим собственному числу
называется собственным вектором матрицы A, соответствующим собственному числу 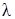 .
.
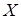 — собственный вектор матрицы
— собственный вектор матрицы 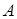 , соответствующий собственному числу
, соответствующий собственному числу 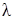 ; тогда для любого вещественного числа
; тогда для любого вещественного числа 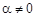 столбец
столбец 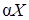 также является собственным вектором матрицы
также является собственным вектором матрицы 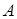 , соответствующим этому же собственному числу. Действительно, по свойствам матричных операций
, соответствующим этому же собственному числу. Действительно, по свойствам матричных операций
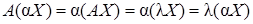 .
.
Если 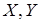 — собственные векторы матрицы
— собственные векторы матрицы 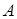 , соответствующие собственному числу
, соответствующие собственному числу 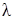 , то столбец
, то столбец 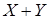 также является собственным вектором матрицы
также является собственным вектором матрицы 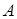 , соответствующим этому же собственному числу. Действительно, по свойствам матричных операций
, соответствующим этому же собственному числу. Действительно, по свойствам матричных операций
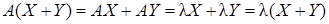 .
.
Рассмотрим систему уравнений, равносильную матричному равенству 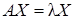 :
:
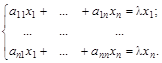
или, перенося свободные члены влево,
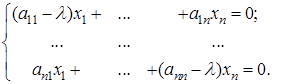 (3)
(3)
Система (3) заведомо имеет, по меньшей мере, одно — нулевое — решение:  . Для того чтобы она имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен 0.
. Для того чтобы она имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен 0.
Таким образом, получаем уравнение для нахождения собственных чисел
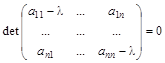 , (4)
, (4)
или в матричных обозначениях
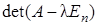 .
.
Уравнение (1.2) называется характеристическим уравнением матрицы 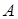 . Для нахождения собственных векторов надо значения l, найденные при решении характеристического уравнения (4), подставить в систему (3) и решить её методом Гаусса.
. Для нахождения собственных векторов надо значения l, найденные при решении характеристического уравнения (4), подставить в систему (3) и решить её методом Гаусса.
ВЕКТОРНАЯ АЛГЕБРА
2.1. Основные понятия
Величины, которые полностью характеризуются одним числом, называются скалярными величинами, или просто скалярами. Примерами скалярных величин могут служить масса судна с грузом, водоизмещение судна, температура воздуха, угол между направлением движения судна и направлением на север.
Наряду со скалярами рассматривают величины, для полной характеристики которых одного числа недостаточно, требуется указать ещё их направление. Примерами таких величин служат скорость судна, сила удара при швартовке и т.д. Такие величины называются векторными.
 |
Рис. 1
Вектором называется направленный отрезок. Направление задаётся указанием, какая из двух граничных точек отрезка считается начальной, а какая, соответственно, конечной.
Если точка 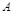 является начальной, а
является начальной, а 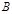 конечной, то вектор направлен от
конечной, то вектор направлен от 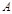 к
к 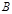 (рис. 1). Обозначения вектора;
(рис. 1). Обозначения вектора; 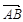 ,
, 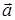 .
.
Модулем вектора 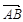 называется длина отрезка
называется длина отрезка 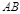 . Обозначения:
. Обозначения: 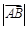 ,
, 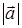 .
.
Нулевой вектор 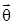 —это вектор, начало и конец которого совпадают; его модуль равен нулю, а направление не определено.
—это вектор, начало и конец которого совпадают; его модуль равен нулю, а направление не определено.
Два вектора в пространстве или плоскости называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Два вектора называются равными, если они коллинеарны, имеют одинаковое направление и их модули равны.
Вектор 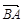 называется противоположным вектору
называется противоположным вектору 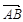 и обозначается
и обозначается 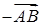 .
.
Единичным вектором (или ортом), называется вектор, модуль которого равен единице. Единичный вектор 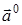 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 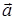 , называется ортом этого направления.
, называется ортом этого направления.
2.2. Линейные операции с векторами
Сумма 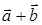 векторов
векторов 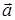 и
и 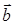 определяется по правилу треугольника или параллелограмма (рис. 9.2 и 9.3).
определяется по правилу треугольника или параллелограмма (рис. 9.2 и 9.3).
Сумма двух неколлинеарных векторов может быть также найдена по правилу параллелограмма (рис. 9.3).
Для сложения векторов справедливы следующие свойства:
1)  — коммутативность сложения;
— коммутативность сложения;
2) 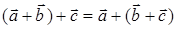 — ассоциативность сложения;
— ассоциативность сложения;
3) 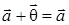 ;
;
4) 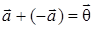 .
.
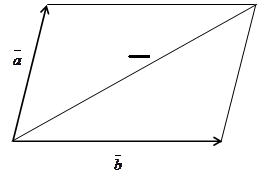 |
Рис. 2.


Рис.3.
Разностью 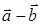 векторов
векторов 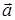 и
и 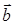 называется вектор
называется вектор 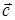 , для которого
, для которого 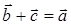 . При этом
. При этом 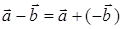 (рис. 4).
(рис. 4).
|
|
|

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!