На практике мы наиболее часто сталкиваемся с геометрическим воздействием на течение жидкости, когда имеет место только изменение площади проходного сечения канала по длине. Это прежде всего сопла и диффузоры реактивных двигателей, компрессоров и турбин. Изучение этих течений как одномерных при условии отсутствия других воздействий является наиболее простым для анализа.
При движении несжимаемой жидкости в канале переменного сечения скорость потока изменяется обратно пропорционально площади. Это следует из уравнения неразрывности (1.26)[1]. В случае движения газа по изменению площади сечения еще нельзя судить об изменении скорости, если заранее неизвестно, как меняется плотность. Лишь только при малых скоростях, когда изменение плотности невелико, можно сделать приближенную качественную оценку по аналогии с несжимаемой жидкостью.
Рассмотрим связь между скоростью потока и площадью поперечного сечения для энергоизолированного изоэнтропного течения.
Из условия постоянства массового расхода по длине потока для изолированного одномерного течения (для элементарной струйки) уравнение неразрывности (уравнение расхода)
m =ρ wF = Const,
где m – массовый расход, ρ – плотность, w – скорость жидкости, а F – площадь проходного сечения канала.
Продифференцировав уравнение неразрывности (расхода)
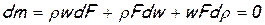
и разделив почленно на m =ρ wF, получим дифференциальное уравнение неразрывности
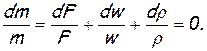
Исключим из этого уравнения член, учитывающий изменение плотности. С этой целью преобразуем уравнение Бернулли для изолированного течения (для элементарной струйки): 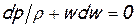 , с учетом выражения для скорости звука a2=dp/dρ:
, с учетом выражения для скорости звука a2=dp/dρ:
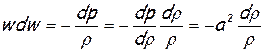 или
или 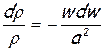 .
.
Подставив последнее выражение для плотности в дифференциальное уравнение неразрывности, получим частный случай уравнения обращения воздействия для случая геометрического воздействия на течение жидкости – уравнение Гюгонио:
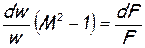 ,
,
которое показывает, что дозвуковой поток (при M <1) ускоряется (d w >0) в сужающихся каналах (dF<0) и тормозится (d w <0) в расширяющихся каналах (dF>0), а сверхзвуковой поток (при M>1) наоборот - ускоряется (d w >0) в расширяющихся каналах (dF>0) и тормозится (d w <0) в сужающихся каналах (dF<0).
Очевидно также, что если площадь канала остается постоянной (dF=0), то и в дозвуковом и в сверхзвуковом потоке скорость должна сохраняться неизменной по длине канала (d w =0).
Для того, чтобы разогнать дозвуковой поток до сверхзвуковой скорости в трубе переменного сечения, необходимо сначала суживать трубу, а затем расширять. Переход через скорость звука (M=1) может произойти только в минимальном сечении трубы, так как при M=1 только при dF=0 скорость w может иметь конечное значение (не становится бесконечно большой). Такие трубы или каналы называются соплами Лаваля (по имени шведского инженера X. Y. Лаваля впервые применившего сопла в паровых турбинах для получения сверхзвуковых скоростей).
Еще один вариант!
«Из уравнения расхода путем логарифмирования и дифференцирования получаем
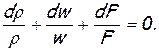 (2.76)
(2.76)
Здесь, чтобы исключить плотность, нужно сделать следующие преобразования. Поделив числитель и знаменатель первого слагаемого на dр, заменим 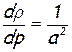 согласно (2.34), а
согласно (2.34), а 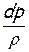 выразим из уравнения Бернулли для данного вида течения (2.24), а именно:
выразим из уравнения Бернулли для данного вида течения (2.24), а именно:
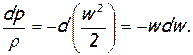
Тогда
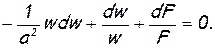
После небольших преобразований получим
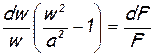
и окончательно
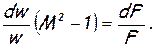 (2.77)
(2.77)
Эта зависимость называется уравнением Гюгонио.
Анализ этого уравнения производится так. Задавая число М (М<1 или М>1) и изменение площади (увеличение dF>0 или уменьшение dF<0), исследуют, при каком знаке — положительном или отрицательном — у dw обе части уравнения (2.77) будут находиться в соответствии, т.е. будут иметь одинаковые знаки. Если dw>0, то скорость нарастает, если dw<0, то она падает. Канал, в котором поток движется с увеличением скорости, называют конфузором или соплом, а при движении потока с уменьшением скорости – диффузором [2].
Анализ уравнения (2.77) дает четыре вида течения:
1. М<1 dF < 0 dw > 0 конфузор;
2. М<1 dF > 0 dw < 0 диффузор;
3. М>1 dF < 0 dw < 0 диффузор;
4. М>1 dF > 0 dw > 0 конфузор.
Если дозвуковой поток необходимо перевести в сверхзвуковой или, наоборот, сверхзвуковой перевести непрерывным путем в дозвуковой, то канал должен иметь более сложную форму. Его входная часть должна быть суживающейся, а выходная — расширяющейся. В том месте, где скорость потока переходит через скорость звука, т.е. М=1, dF=0, следовательно, площадь поперечного сечения проходит через минимум и канал образует горло. Таким образом, в энергоизолированном изоэнтропном потоке критическое сечение (w=а) совпадает с горлом канала.
Каналы с суживающейся входной и расширяющейся выходной частью широко применяются в технике. Если они предназначаются для преобразования дозвукового потока в сверх звуковой, то называются соплами Лаваля, при обратном действии — преобразовании сверхзвукового потока в дозвуковой — сверхзвуковыми диффузорами.
& (Виноградов) с.65 … 67



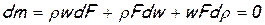
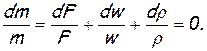
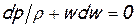 , с учетом выражения для скорости звука a2=dp/dρ:
, с учетом выражения для скорости звука a2=dp/dρ: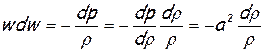 или
или 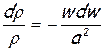 .
.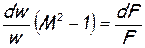 ,
,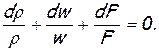 (2.76)
(2.76)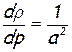 согласно (2.34), а
согласно (2.34), а 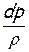 выразим из уравнения Бернулли для данного вида течения (2.24), а именно:
выразим из уравнения Бернулли для данного вида течения (2.24), а именно: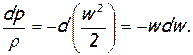
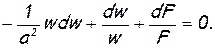
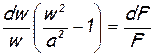
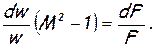 (2.77)
(2.77)

