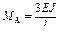Пигунов, В. В.
П32 Строительная механика стержневых вагонных конструкций: учеб.-метод. пособие для студентов всех форм обучения специальности 1-37 02 02 «Подвижной состав железнодорожного транспорта» / В. В. Пигунов, А. В. Пигунов; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. – Гомель: БелГУТ, 2012. – 125 с..
ISBN 978-985-468-898-5
Рассмотрены расчетные модели вагонных конструкций и общие методы расчета статически неопределимых стержневых несущих систем вагонов.
Предназначено для студентов всех форм обучения специальности «Подвижной состав железнодорожного транспорта».
УДК 62 4. 04:629.4
ББК 3 8. 112
ISBN 978-985-468-898-5 © Пигунов В. В., Пигунов А. В., 2012
© Оформление. УО «БелГУТ», 2012
ОГЛАВЛЕНИЕ
| Введение ……….……………………………………………………………………………….
| 4
|
| 1 Расчетные модели вагонных конструкций …...………….....
| 6
|
| 1.1 Классификация вагонных конструкций и действующих на них нагрузок …..…….…
| 6
|
| 1.2 Реальные вагонные конструкции и их расчетные схемы …………………………..….
| 9
|
| 1.3 Методы оценки несущей способности вагонных конструкций …………………...….
| 16
|
| 2 Кинематический анализ стержневых систем …………………………………………..
| 189
|
| 2.1 Общие сведения о стержневых системах ………………………………………………
| 18
|
| 2.2 Анализ геометрической неизменяемости стержневых систем …..………………...….
| 20
|
| 3 Расчет статически неопределимых стержневых систем методом сил..……..……….
| 31
|
| 3.1 Статически неопределимые системы и особенности их расчета …….…………….…
| 31
|
| 3.2 Установление степени статической неопределимости ……………………………..….
| 32
|
| .3.3 Выбор основной системы ………..……………………………………………………...
| 40
|
| 3.4 Канонические уравнения метода сил …………………………………………………...
| 42
|
| 3.5 Определение коэффициентов и свободных членов. Решение канонических
|
|
| уравнений ……………………………………………………………………………..…..
| 43
|
| 3.6 Построение окончательных эпюр внутренних сил для заданной системы …………..
| 47
|
| 3.7 Выбор рациональной основной системы.…………………………………………..….
| 52
|
| 3.8 Способы упрощения расчета симметричных статически неопределимых
| 55
|
| стержневых систем …………………………………………………………………..…..
|
|
| 3.8.1 Выбор симметричной основной системы …………….…………………….…….
| 55
|
| 3.8.2 Преобразование нагрузки ………………………………………………………….
| 57
|
| 3.8.3 Группировка неизвестных ……………………………..………………………….
| 60
|
| 3.8.4 Введение жестких консолей ……………………………………………………….
| 62
|
| 3.9 Общий алгоритм расчета статически неопределимых систем методом сил ….…..….
| 64
|
| 3.10 Определение перемещений от внешней нагрузки в статически неопределимых
|
|
| стержневых системах ……..……………………….………………………………..….
| 70
|
| 3.11 Расчет плоских статически неопределимых стержневых
|
|
| вагонных конструкций …………………………………………………………………
| 74
|
| 3.11.1 Расчет боковой рамы тележки грузового вагона на вертикальные силы ……
| 74
|
| 3.11.2 Расчет рамы платформы на продольные силы ………………………………..
| 87
|
| 3.12 Расчет пространственных и плоскопространственных статически неопределимых
|
|
| стержневых вагонных конструкций …………………………………………………..
| 90
|
| 4 Расчет статически неопределимых стержневых систем методом перемещений ….
| 99
|
| 4.1 Установление степени кинематической неопределимости ………....……………..….
| 99
|
| 4.2 Выбор основной системы …………………………………………………………....….
| 102
|
| 4.3 Составление канонических уравнений …………………………………………………
| 106
|
| 4.4 Определение коэффициентов и свободных членов. Решение канонических
|
|
| уравнений ……………………………………………………………………………..…..
| 107
|
| 4.5 Построение окончательных эпюр внутренних сил для заданной системы …………..
| 109
|
| 4.6 Пример расчета статически неопределимой системы методом перемещений …..…
| 110
|
| Список литературы ………………………………..…………………………………………
| 124
|
ВВЕДЕНИЕ
Строительная механика – наука о принципах и методах расчета конструкций на прочность, жесткость и устойчивость при статических и динамических воздействиях.
Она рассматривает те же вопросы, что и сопротивление материалов, только объектом исследования является не отдельный элемент конструкции, а совокупность многих элементов, образующих конструкцию.
Особенностью строительной механики вагонов является то, что здесь эти вопросы рассматриваются применительно к вагонным конструкциям, к которым относятся кузова вагонов, а также отдельные части кузовов, тележек и др.
Любая проектируемая конструкция, в том числе и конструкция вагона, должна удовлетворять требованиям прочности, жесткости, устойчивости и экономичности.
Достаточная прочность и жесткость позволяют вагону воспринимать действующие на него эксплуатационные нагрузки без повреждений и недопустимых изменений формы.
При этом прочность вагонной конструкции должна обеспечиваться при возможно меньшей затрате металла, то есть конструкция должна удовлетворять требованиям экономичности. В связи с этим весьма важное значение имеет совершенствование методов расчета.
По мере совершенствование методов расчета на прочность конструкции проектируются все более легкими и гибкими. Вследствие этого появляется необходимость проверки их на жесткость и устойчивость.
Рассчитывают конструкцию исходя из внешних воздействий на нее и ее сопротивления этим воздействиям. Внешние воздействия разделяют на силовые, температурные и дислокационные (задаваемые перемещения из-за неточности изготовления). Сопротивление представляет собой основную функцию несущей конструкции. Оно определяется физическими характеристиками и геометрическими параметрами элементов и их соединений.
Строительная механика является теоретической базой для создания надежных, прочных и экономичных конструкций.
Предлагаемое учебно-методическое пособие является первой частью курса «Строительная механика вагонов».
Стержневые системы, которые рассматриваются в данном пособии, находят достаточно широкое применение в несущих конструкциях вагонов.
В то же время специалисту в своей практической деятельности приходится иметь дело с более сложными системами, в состав которых помимо стержней входят элементы и других типов – пластины и оболочки и др..
Как известно, при расчете таких сложных систем широко применяется метод конечных элементов.
В связи с этим при изложении методов расчета стержневых систем существенное внимание уделено вопросам, которые играют фундаментальную роль и в расчетах более сложных, нестержневых конструкций. Речь идет о методе перемещений, который является базой для метода конечных элементов.
Пособие предназначено для студентов всех форм обучения, но может быть использовано также и инженерно-техническими работниками в их практической деятельности.
РАСЧЕТНЫЕ МОДЕЛИ
ВАГОННЫХ Конструкций
Выбор основной системы
Следующий этап расчета статически неопределимых систем по методу сил – выбор так называемой основной системы.
Основная система используется для раскрытия статической неопределимости.
Основная система – это статически определимая и геометрически неизменяемая система.
Она получается из заданной системы в два этапа:
1) устранением всех лишних связей;
2) введением взамен удаленных связей их реакций 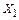 , …,
, …, 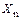 .
.
П р и м е ч а н и я
1 Это два условия эквивалентности заданной и основной систем.
2 Реакции связей – это неизвестные усилия, приложенные по направлению отброшенных связей.
3 Количество лишних связей равно степени статической неопределимости системы.
Для любой статически неопределимой системы всегда имеется множество вариантов основной системы. Трудоемкость расчета зависит от выбора рационального варианта основной системы.
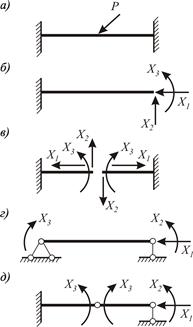
Основные способы получения основных систем, т.е. способы устранения лишних связей, рассмотрим на примере простейшей статически неопределимой системы – балки с жесткими заделками по концам, которая имеет три лишних связи (рисунок 3.11, а).
1 Удаление лишних внешних (опорных) связей (рисунок 3.11, б).
2 Удаление лишних внутренних связей путем рассечения стержня (рисунок 3.11, в).
3 Переход к другим видам опорных связей (рисунок 3.11, г).
4 Удаление лишних внутренних связей посредством введения шарниров, (рисунок 3.11, д).
5 Комбинированный – сочетание указанных выше способов (см. рисунок 3.11, д).
Поясним эти способы.
Первый способ реализуется удалением правой заделки, которая эквивалентна трем кинематическим связям, препятствующим двум линейным перемещениям и повороту опорного сечения стержня. Удаленные связи заменены их реакциями: продольной силой Х 1, поперечной силой Х 2 и изгибающим моментом Х 3. В результате получена статически определимая система – консоль (балка, защемленная одним концом).
Второй способ предполагает рассечение стержня. Разрезая стержень, мы удаляем три внутренних связи, так как позволяем смежным сечениям поворачиваться и смещаться в двух направлениях относительно друг друга. Поэтому действие отброшенных связей заменяем их реакциями Х 1, Х 2 и Х 3.
|
| Рисунок 3.11 – Основные способы получения основных систем:
а – исходная система; б - д – варианты основных систем
|
Отметим, что для внутренних связей силы (реакции) Х 1, Х 2 и Х 3 являются взаимными (групповыми). К смежным сечениям прикладываются равные и противоположные друг другу пары сил Х 1, Х 2 и Х 3. Основная система представляет собой две статически определимые консоли.
Третий способ характеризуется тем, что жесткие заделки заменены на шарнирно-неподвижную и шарнирно-подвижную опоры. При переходе к шарнирно-подвижной опоре снимается две связи – появляется возможность линейного смещения и поворота, при переходе к шарнирно-неподвижной опоре устраняется одна связь – становится возможным угловое смещение. Соответственно этим смещениям вводятся реакции. Полученная основная система представляет собой статически определимую двухопорную балку.
Четвертый способ основан на включении шарнира, который устраняет связь, препятствующую повороту смежных сечений, и понижает степень статической неопределимости на единицу. Введенный шарнир устранил только одну связь, поэтому для снятия еще двух связей правую заделку заменяем шарнирно-подвижной опорой. Поскольку введенные шарниры частично устраняют внутренние связи, то данный способ применяют, как правило, в сочетании с другими.
П р и м е ч а н и я
1. При разрезании плоского стержня (контура) удаляются три связи: две связи, препятствующие взаимным линейным перемещениям; одна связь, препятствующая взаимному угловому перемещению сечений контура в месте разреза.
2. При удалении шарнира удаляются две внутренние линейные связи.
3. При врезании в стержень (контур) шарнира удаляется одна связь (угловая).
При удалении связей системы необходимо следить за тем, чтобы получаемая конструкция была геометрически неизменяемая. Следовательно, не всякая система с удаленными связями может быть принята как основная.
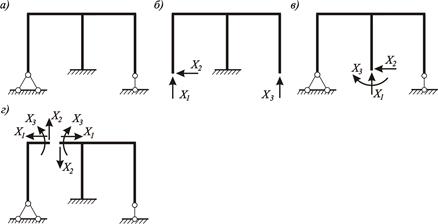
На рисунках 3.12, а – г приведены рама, которая имеет три лишних связи, и несколько возможных вариантов основных систем для нее. Последний вариант – пример неправильного выбора основной системы. В этом варианте рама расчленена на две системы: левая – имеет две опорные связи и поэтому является геометрически изменяемой, правая – четыре опорных связи, т.е. статически неопределима.
| Рисунок 3.12 – К выбору основных систем:
а – исходная система; б-г – варианты основных систем
| |
Устранение лишних связей не изменяет внутренних усилий, возникающих в системе, и ее деформаций, так как к ней прикладываются реакции отброшенных связей. Поэтому обе эти системы будут эквивалентными в статическом и кинематическом отношениях.
Таким образом, расчет статически неопределимых систем методом сил сводится искусственным путем к расчету равноценной по возникающим усилиям и перемещениям статически определимой основной системы.
Группировка неизвестных
При расчете многопролетных симметричных рам не всегда удается разместить все неизвестные в сечениях по оси симметрии.
В этом случае для получения симметричных и кососимметричных эпюр целесообразно принимать групповые неизвестные, расположив их в различных симметрично расположенных точках.
Проиллюстрируем данный способ для двухпролетной рамы, приведенной на рисунке 3.27, а.
При традиционном способе решения основная система и единичные эпюры показаны на рисунках 3.27, б–г.
При использовании традиционного способа все побочные коэффициенты 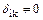 .
.
При использовании способа группировки неизвестных упрощение расчета обеспечивается тем, что в качестве лишних неизвестных принимают не отдельные силы, а группы сил.

Рисунок 3.27 – Традиционный способ решения системы:
а – исходная система; б – основная система; в, г – единичные эпюры моментов
П р и м е ч а н и е – Групповые неизвестные подбирают так, чтобы получающиеся от их действия эпюры были ортогональными (симметричными и кососимметричными).
Для рамы, изображенной на рисунке 3.27, а, реакции удаленных связей, которые обозначим как 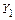 и
и 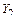 , заменим эквивалентными им новыми неизвестными – парами симметричных
, заменим эквивалентными им новыми неизвестными – парами симметричных 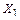 и кососимметричных
и кососимметричных  сил. Реакцию левой опоры
сил. Реакцию левой опоры 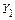 представим суммой сил
представим суммой сил 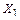 и
и  , а реакция правой опоры
, а реакция правой опоры  – разностью этих сил (рисунок 3.28, а), т.е.
– разностью этих сил (рисунок 3.28, а), т.е.
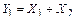 ;
; 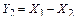 .
.
П р и м е ч а н и е – Неизвестное 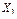 представляет собой две симметрично расположенные силы, а
представляет собой две симметрично расположенные силы, а 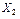 – две кососимметричные силы.
– две кососимметричные силы.
Эпюры моментов от единичных групповых силовых факторов показаны на рисунках 3.28, б, в.
В результате перемножения эпюр 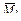 и
и 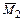 получаем
получаем  . Это следует также из правила 1.
. Это следует также из правила 1.
В результате получаем канонические уравнения с полностью разделенными неизвестными, каждое из которых содержит только по одному лишнему неизвестному
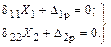
Использование групповых неизвестных значительно упрощает расчет симметричных рам с большим числом лишних неизвестных.
П р и м е ч а н и е – Сущность способа группировки неизвестных состоит в том, что в качестве неизвестных принимают не отдельные силы, а группы сил, составленные так, чтобы получающиеся от их действия эпюры были ортогональными.

Рисунок 3.28 – Упрощение расчета рамы с помощью способа группировки
неизвестных:
а – основная система; б, в – единичные эпюры моментов
Введение жестких консолей
Этот способ применяется для рам, имеющих замкнутый контур (см. рисунки 3.1, в и 3.2, в), и позволяет получать системы канонических уравнений с полностью разделенными неизвестными
Рассмотрим систему, показанную на рисунке 3.1, в.
В случае выбора традиционной симметричной основной системы (рисунок 3.29, а) для нее будет справедлива система уравнений (3.25), в которой 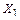 – кососимметричный силовой фактор,
– кососимметричный силовой фактор, 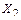 ,
, 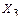 – симметричные силовые факторы.
– симметричные силовые факторы.
Тогда, побочные коэффициенты  и
и 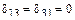 .
.
В полученных уравнениях все побочные коэффициенты, кроме коэффициентов  и
и 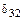 равны нулю, т.е.
равны нулю, т.е. 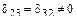 .
.
Для получения системы уравнений с полностью разделенными неизвестными необходимо также обратить в нуль и коэффициенты 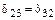 с индексами, принадлежащими симметричным факторам.
с индексами, принадлежащими симметричным факторам.
Коэффициенты 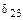 и
и  являются результатом перемножения единичных эпюр
являются результатом перемножения единичных эпюр 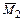 и
и 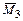 .
.
Для ортогонализации (обращения в нуль) этих эпюр необходимо перенести неизвестные в точку C, называемую упругим центром, с помощью жестких консолей.
П р и м е ч а н и е – При наличии у рамы одной оси симметрии упругий центр будет лежать на этой оси и надо будет определить только одну его координату zо.
Для рамы, имеющей две оси симметрии, упругий центр будет находиться на пересечении этих осей.

Рисунок 3.29 – Упрощение расчета рамы введением жестких консолей:
а – симметричная основная система; б – основная система с введенными жесткими консолями; в, г – единичные эпюры моментов
На рисунках 3.29, б-г приведены основная система, полученная с помощью введения абсолютно жестких консолей и перемещения неизвестных силовых факторов в упругий центр, а также единичные эпюры моментов 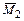 и
и 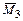 .
.
Коэффициент 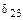 , определяемый как результат перемножения этих эпюр, будет равен
, определяемый как результат перемножения этих эпюр, будет равен
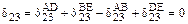 ,
,
где 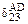 ,
,  – результат перемножения эпюр
– результат перемножения эпюр 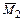 и
и 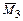 соответственно на участках AD и BE;
соответственно на участках AD и BE;
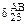 ,
,  – то же на участках AB и DE.
– то же на участках AB и DE.
Проанализируем результат перемножения эпюр по всем участкам рамы.
На участках AD и BE коэффициент  будет равен нулю (
будет равен нулю (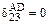 и
и 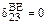 ), поскольку здесь перемножаются симметричные эпюры
), поскольку здесь перемножаются симметричные эпюры 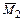 и кососимметричные
и кососимметричные 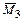 .
.
На участках AB и DE эпюры 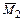 и
и  одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем
одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем 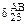 и
и  одинаковые по величине, но с разными знаками. При суммировании они дают нуль.
одинаковые по величине, но с разными знаками. При суммировании они дают нуль.
Таким образом, в рассматриваемом случае эпюры 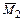 и
и 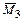 являются ортогональными.
являются ортогональными.
Тогда канонические уравнения примут вид
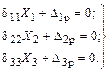
Таким образом, при переносе неизвестных в упругий центр обращается в нуль единственное оставшееся побочное перемещение 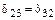 и вместо системы уравнений получается 3 независимых уравнения.
и вместо системы уравнений получается 3 независимых уравнения.
Методом сил
Рассмотрим алгоритм расчета статически неопределимых систем на примере рамы, показанной на рисунке 3.30, а. В качестве примера выбрана достаточно простая система, позволяющая не перегружать расчет арифметическими выкладками, но в то же время показать особенности расчета, характерные и для более сложных систем.
Установление степени статической неопределимости. Для рассматриваемой системы степень статической неопределимости n = 3.
Выбор основной системы. Для выбора основной системы необходимо в заданной системе удалить три лишних связи. При этом получаемая основная система должна быть статически определимой и геометрически неизменяемой.
Заданная система является симметричной конструкцией, на которую действует симметричная нагрузка. Поэтому целесообразно выбирать симметричную основную систему.
Рассматриваемая система три раза статически неопределима, но условия симметрии конструкции и загружения позволяют сократить число лишних неизвестных до двух (правило 3).
Основную систему получаем рассечением стержня по оси симметрии и введением в местах разреза реакций удаленных связей – симметричных силовых факторов Х 1 и Х 2 (рисунок 3.30, б). Кососимметричный силовой фактор Х 3 (поперечная сила) в плоскости симметрии будет равен нулю.
П р и м е ч а н и е – Направление действия реакций отброшенных связей принимают произвольно.
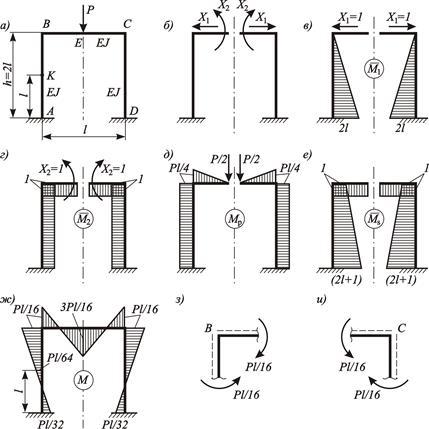
Рисунок 3.30 – К расчету статически неопределимой системы:
а – исходная система; б – основная система; в, г – единичные эпюры моментов;
д – грузовая эпюра моментов; е – суммарная единичная эпюра моментов;
ж – окончательная эпюра моментов; з, и – вырезанные узлы
Составление канонических уравнений. Для двух неизвестных система канонических уравнений будет иметь вид:
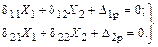
Определение коэффициентов и свободных членов канонических уравнений. Для вычисления коэффициента 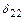 и свободного члена
и свободного члена 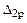 :
:
1) строим эпюры изгибающих моментов: единичные 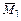 ,
, 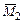 (от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую
(от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую 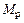 (от внешней нагрузки Р);
(от внешней нагрузки Р);
2) перемножаем эпюры по формулам, приведенным в п. 3.5.
П р и м е ч а н и е – Для упрощения расчета ограничимся рассмотрением только эпюр изгибающих моментов.
При построении эпюр основную систему поочередно нагружаем усилиями Х 1 = 1, Х 2 = 1 и внешней нагрузкой Р. Построенные эпюры моментов 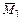 ,
, 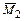 и
и 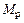 приведены на рисунках 3.30, в–д.
приведены на рисунках 3.30, в–д.
Тогда:
коэффициент 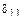 (результат перемножения эпюры
(результат перемножения эпюры 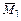 саму на себя)
саму на себя)
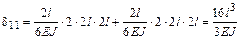 ;
;
коэффициент 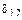 (результат перемножения эпюр
(результат перемножения эпюр 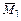 и
и 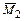 )
)
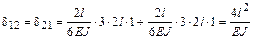 ;
;
коэффициент 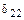 (результат перемножения эпюры
(результат перемножения эпюры 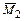 саму на себя)
саму на себя)
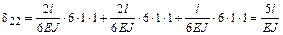 ;
;
свободный член 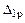 (результат перемножения эпюр
(результат перемножения эпюр 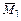 и
и 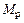 )
)
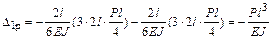 ;
;
свободный член 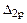 (результат перемножения эпюр
(результат перемножения эпюр 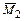 и
и 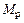 )
)
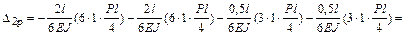
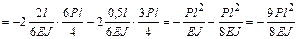 .
.
Для контроля правильности определения коэффициентов и свободных членов строим суммарную единичную эпюру 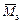 (рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).
(рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).
Перемножаем суммарную эпюру саму на себя (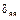 ) и на грузовую (
) и на грузовую (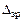 ):
):
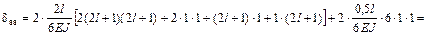
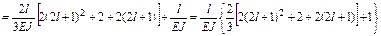 ;
;
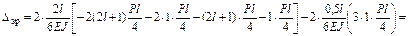
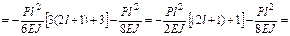
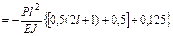 .
.
Проверку коэффициентов и свободных членов выполним для l = 1 м.
Тогда
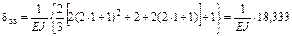 ;
;
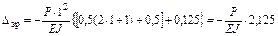 .
.
Определяем:
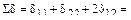
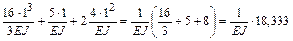 .
.
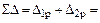
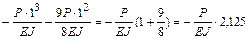 .
.
Поскольку 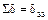 и
и 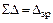 , коэффициенты и свободные члены определены правильно.
, коэффициенты и свободные члены определены правильно.
Решение канонических уравнений. Система канонических уравнений имеет вид:
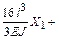
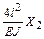
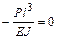 ;
;
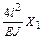
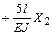
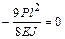 .
.
Умножая все уравнения на EJ, получим коэффициенты и свободные члены окончательной системы канонических уравнений:
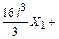
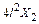
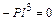 ;
;
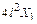
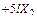
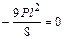 .
.
Решая канонические уравнения, находим значения неизвестных: 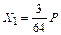 ,
, 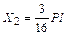 .
.
Для проверки правильности вычисления неизвестных подставляем найденные значения Х 1 и Х 2 в канонические уравнения:
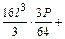
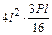
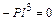 ;
;
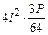
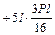
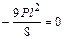 .
.
Построение окончательной эпюры моментов для заданной системы. Ординаты окончательной эпюры изгибающих моментов определяем по формуле (3.18).
Для построения окончательной эпюры изгибающих моментов ординаты единичных эпюр 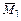 и
и 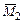 умножаем на соответствующие значения лишних неизвестных
умножаем на соответствующие значения лишних неизвестных 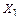 и
и 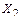 и складываем с ординатами грузовой эпюры
и складываем с ординатами грузовой эпюры 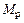 . Суммирование ординат производим по характерным точкам (А, В, С, D, Е) рамы:
. Суммирование ординат производим по характерным точкам (А, В, С, D, Е) рамы:
стержень (стойка) АВ –
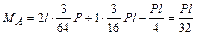 ;
;
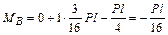 ;
;
стержень (ригель) ВС –
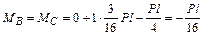 ;
;
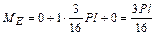 ;
;
стержень (стойка) С D –
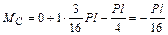 ;
;
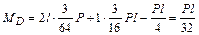 .
.
П р и м е ч а н и е – При вычислении ординат окончательной эпюры 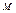 необходимо учитывать знаки силовых факторов
необходимо учитывать знаки силовых факторов 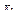 и
и 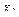 и моментов
и моментов 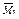 ,
, 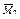 и
и 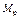 . Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
. Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
Окончательная эпюра изгибающих моментов показана на рисунке 3.30, ж).

 Производим проверку правильности построения окончательной эпюры М – статическую и кинематическую.
Производим проверку правильности построения окончательной эпюры М – статическую и кинематическую.
Для выполнения статической проверки вырезаем жесткие узлы рамы (кроме опорных), прикладываем все действующеие в них моменты и проверяем условие равновесия узла 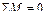 .
.
В рассматриваем случае вырезаем узлы В и С (рисунки 3.30, з, и):
узел В: 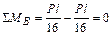 ;
;
узел С: 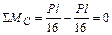 .
.
П р и м е ч а н и е – Знак ординаты эпюры М определяется стрелкой дуги окружности около узла, направленной так, чтобы вызвать растяжение в элементе со стороны ординат эпюры моментов.
Выполнение условия равновесия узлов является необходимым, но недостаточным.
Достаточным условием правильности построения окончательной эпюры М является кинематическая проверка по условию (3.19).
Для этого перемножим окончательную М и суммарную единичную 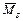 эпюры:
эпюры:
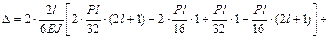
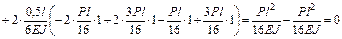 .
.
Поскольку 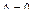 , условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.
, условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.
Вагонных конструкций
Особенность расчета: в сечениях плоской стержневой системы возникают 3 внутренних силовых фактора, действующих в ее плоскости (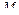 ,
, 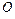 , N).
, N).
В качестве примера рассмотрим расчеты боковой рамы тележки грузового вагона на вертикальные силы и рамы платформы на продольные силы.
Выбор основной системы
Основная система метода перемещений должна быть кинематически определимой. Чтобы выполнить это требование узлы рамы закрепляют от поворотов и линейных смещений введением дополнительных связей.
Основную систему получают из заданной (см. рисунок 4.1):
1) введением дополнительных (фиктивных) связей, устраняющих угловые и линейные перемещения узлов (рисунок 4.6, а);
2) заданием введенным связям соответствующих угловых и линейных перемещений 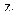 (рисунок 4.6, б).
(рисунок 4.6, б).
П р и м е ч а н и е – Общее число введенных в основную систему связей равно, естественно, числу неизвестных метода перемещений.

Рисунок 4.6 – К выбору основной системы метода перемещений:
а – рама с введенными дополнительными связями; б – основная система
В качестве дополнительных вводятся следующие связи:
угловая связь («плавающая заделка») – вводится во все жесткие узлы для устранения их поворотов (угловых перемещений);
линейная связь – вводится в необходимые места заданной системы для устранения линейных перемещений узлов (об этом информирует шарнирная система).
В рассматриваемом случае две угловые связи («плавающие заделки») с номерами 1 и 2 вводятся для устранения поворота жестких узлов В и С, линейная связь (номер 3) – для устранения линейных перемещений этих же узлов.
П р и м е ч а н и е – Заделка называется «плавающей», поскольку такая связь оказывает препятствие лишь повороту узла, но не лишает его линейной подвижности.
Кинематическая эквивалентность основной и заданной систем достигается тем, что связям одновременно с их введением задают соответствующие угловые и линейные перемещения 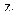 .
.
На рисунке 4.6 через 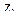 ,
,  и
и  обозначены заданные перемещения введенных связей (показаны стрелками на основной системе).
обозначены заданные перемещения введенных связей (показаны стрелками на основной системе).
П р и м е ч а н и е:
1 Заданные перемещения 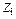 введенных связей имеют такой же индекс, как и номер фиктивной связи. В рассматриваемом случае
введенных связей имеют такой же индекс, как и номер фиктивной связи. В рассматриваемом случае 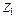 ,
,  – угловые перемещения узлов В и С, устраняемые заделками 1 и 2;
– угловые перемещения узлов В и С, устраняемые заделками 1 и 2; 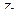 – линейное перемещение узлов В и С, устраняемое стержнем 3.
– линейное перемещение узлов В и С, устраняемое стержнем 3.
2 Углы поворота введенных связей (в нашем случае 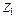 и
и 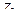 ) условно задаются по часовой стрелке, линейные перемещения (в нашем случае
) условно задаются по часовой стрелке, линейные перемещения (в нашем случае 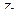 ) – слева – направо.
) – слева – направо.
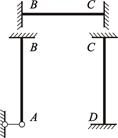
|
| Рисунок 4.7 – Представление основной системы совокупностью статически неопределимых балок
|
Таким образом, расчету подлежит не заданная система, а преобразованная (основная) система, которая должна быть эквивалентна ей в статическом и кинематическом отношениях.
Введенные связи расчленяют получаемую основную систему на отдельные простейшие статически неопределимые балки – конечные элементы (рисунок 4.7). Каждая из этих балок хорошо изучена и результаты их расчета на стандартные воздействия приводятся в справочных данных (таблица 4.1).
Таблица 4.1 – Результаты расчета эпюр изгибающих моментов однопролетных статически неопределимых балок



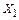 , …,
, …, 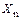 .
.

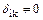 .
.
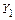 и
и 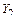 , заменим эквивалентными им новыми неизвестными – парами симметричных
, заменим эквивалентными им новыми неизвестными – парами симметричных 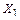 и кососимметричных
и кососимметричных  сил. Реакцию левой опоры
сил. Реакцию левой опоры 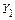 представим суммой сил
представим суммой сил 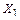 и
и  , а реакция правой опоры
, а реакция правой опоры  – разностью этих сил (рисунок 3.28, а), т.е.
– разностью этих сил (рисунок 3.28, а), т.е.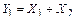 ;
; 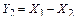 .
.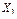 представляет собой две симметрично расположенные силы, а
представляет собой две симметрично расположенные силы, а 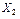 – две кососимметричные силы.
– две кососимметричные силы.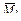 и
и 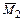 получаем
получаем  . Это следует также из правила 1.
. Это следует также из правила 1.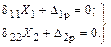

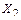 ,
, 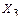 – симметричные силовые факторы.
– симметричные силовые факторы. и
и 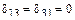 .
. и
и 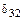 равны нулю, т.е.
равны нулю, т.е. 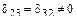 .
.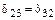 с индексами, принадлежащими симметричным факторам.
с индексами, принадлежащими симметричным факторам.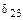 и
и  являются результатом перемножения единичных эпюр
являются результатом перемножения единичных эпюр 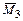 .
.
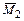 и
и 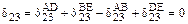 ,
, 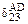 ,
,  – результат перемножения эпюр
– результат перемножения эпюр 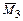 соответственно на участках AD и BE;
соответственно на участках AD и BE;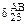 ,
,  – то же на участках AB и DE.
– то же на участках AB и DE. будет равен нулю (
будет равен нулю (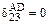 и
и 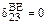 ), поскольку здесь перемножаются симметричные эпюры
), поскольку здесь перемножаются симметричные эпюры 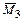 .
. одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем
одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем 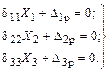

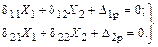
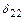 и свободного члена
и свободного члена 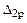 :
: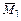 ,
, 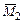 (от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую
(от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую 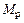 (от внешней нагрузки Р);
(от внешней нагрузки Р);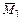 ,
, 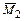 и
и 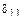 (результат перемножения эпюры
(результат перемножения эпюры 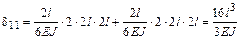 ;
;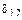 (результат перемножения эпюр
(результат перемножения эпюр 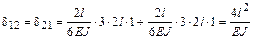 ;
;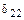 (результат перемножения эпюры
(результат перемножения эпюры 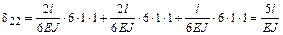 ;
;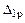 (результат перемножения эпюр
(результат перемножения эпюр 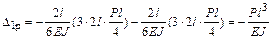 ;
;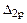 (результат перемножения эпюр
(результат перемножения эпюр 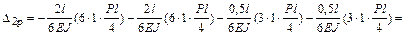
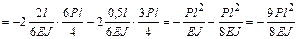 .
.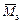 (рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).
(рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).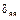 ) и на грузовую (
) и на грузовую (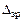 ):
):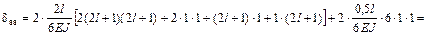
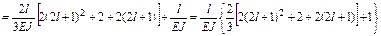 ;
;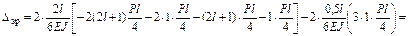
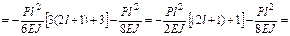
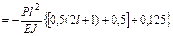 .
.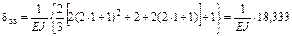 ;
;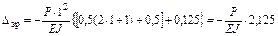 .
.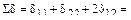
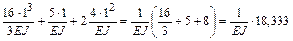 .
.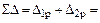
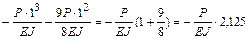 .
.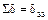 и
и 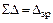 , коэффициенты и свободные члены определены правильно.
, коэффициенты и свободные члены определены правильно.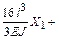
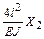
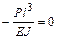 ;
;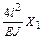
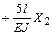
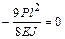 .
.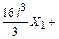
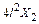
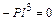 ;
;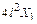
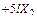
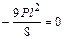 .
.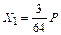 ,
, 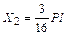 .
.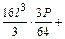
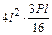
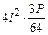
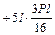
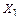 и
и 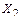 и складываем с ординатами грузовой эпюры
и складываем с ординатами грузовой эпюры 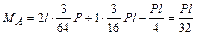 ;
;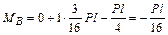 ;
;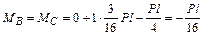 ;
;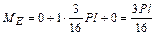 ;
;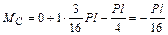 ;
;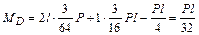 .
.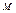 необходимо учитывать знаки силовых факторов
необходимо учитывать знаки силовых факторов 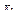 и
и 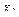 и моментов
и моментов 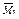 ,
, 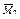 и
и 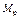 . Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
. Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
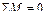 .
.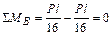 ;
;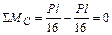 .
.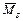 эпюры:
эпюры: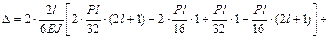
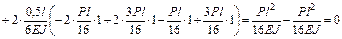 .
.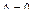 , условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.
, условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.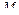 ,
, 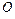 , N).
, N).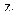 (рисунок 4.6, б).
(рисунок 4.6, б).
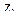 ,
,  и
и 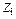 введенных связей имеют такой же индекс, как и номер фиктивной связи. В рассматриваемом случае
введенных связей имеют такой же индекс, как и номер фиктивной связи. В рассматриваемом случае 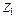 ,
,  – угловые перемещения узлов В и С, устраняемые заделками 1 и 2;
– угловые перемещения узлов В и С, устраняемые заделками 1 и 2; 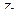 – линейное перемещение узлов В и С, устраняемое стержнем 3.
– линейное перемещение узлов В и С, устраняемое стержнем 3. ) условно задаются по часовой стрелке, линейные перемещения (в нашем случае
) условно задаются по часовой стрелке, линейные перемещения (в нашем случае 


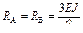 ;
;