Вектор вида 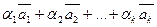 , где
, где  (
(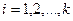 ) – некоторые числа, называется линейной комбинацией данных векторов
) – некоторые числа, называется линейной комбинацией данных векторов 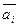 .
.  – коэффициенты линейной комбинации. Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.
– коэффициенты линейной комбинации. Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.
Справедливы следующие теоремы
Т е о р е м а 1. Пусть даны два неколлинеарных вектора 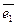 и
и  . Любой компланарный с ними вектор
. Любой компланарный с ними вектор  раскладывается по ним и такое разложение единственно. Т. е.,
раскладывается по ним и такое разложение единственно. Т. е.,  =
=  +
+  , где
, где 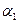 и
и 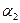 единственные для этого вектора
единственные для этого вектора  вполне определенные числа.
вполне определенные числа.
Т е о р е м а 2. Пусть даны три некомпланарных вектора 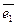 ,
,  и
и  . Любой вектор
. Любой вектор  раскладывается по ним и такое разложение единственно. Т. е.,
раскладывается по ним и такое разложение единственно. Т. е.,  =
=  +
+  +
+ 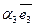 .
.
Базисом в пространстве называются три некомпланарных вектора, взятых в определенном порядке. Базис позволяет однозначно сопоставить вектору упорядоченную тройку чисел 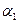 ,
, 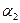 ,
,  - коэффициентов разложения этого вектора по векторам базиса. С другой стороны, каждой упорядоченной тройке чисел при помощи базиса сопоставляется единственный вектор. Если
- коэффициентов разложения этого вектора по векторам базиса. С другой стороны, каждой упорядоченной тройке чисел при помощи базиса сопоставляется единственный вектор. Если 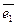 ,
, 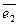 ,
, 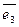 - базис и
- базис и  =
=  +
+  +
+ 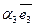 , то числа
, то числа 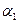 ,
, 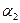 ,
,  называются координатами вектора
называются координатами вектора  в данном базисе, при этом пишут
в данном базисе, при этом пишут  . Аналогично дается определение базиса на плоскости, когда вектор имеет две координаты
. Аналогично дается определение базиса на плоскости, когда вектор имеет две координаты 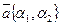 .
.
Действия над векторами, заданными своими координатами:
1.При умножении вектора на число все его координаты умножаются
на это число. Т.е.,  (
( +
+ 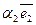 +
+ 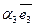 )=
)=  +
+  +
+ 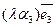 и
и  {
{  ,
, 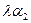 ,
,  }.
}.
2. При сложении векторов складываются их соответствующие координаты. Т. е., если в выбранном базисе 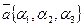 ,
, 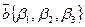 , то
, то  .
.
Аффинные координаты
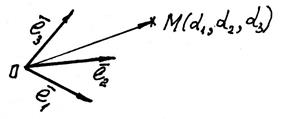
Аффинные координаты в пространстве определяются (рис. 4) заданием базиса
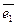
,
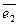
,
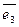
и точки
О – начала координат (
affinis – смежный, соседний).
Рис. 4
Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат: первая – ось абсцисс; вторая – ось ординат; третья – ось аппликат. Плоскости, проходящие через оси координат – координатные плоскости.
Пусть в пространстве задана точка М. 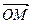 - радиус-вектор точки М. Тогда разложение по векторам базиса
- радиус-вектор точки М. Тогда разложение по векторам базиса 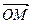 =
= 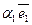 +
+ 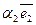 +
+ 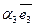 . Аффинными координатами точки М называются координаты - радиус-вектора
. Аффинными координатами точки М называются координаты - радиус-вектора
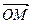 в рассматриваемой системе координат, пишут
в рассматриваемой системе координат, пишут 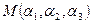 , где
, где 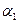 - абсцисса,
- абсцисса, 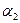 - ордината,
- ордината, 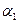 - аппликата точки М. В заданной аффинной системе координат координаты фиксированной точки определяются однозначно. С другой стороны, если задана система координат, то в ней каждой упорядоченной тройке чисел ставится в соответствие единственная точка. Аффинная система координат на плоскости
- аппликата точки М. В заданной аффинной системе координат координаты фиксированной точки определяются однозначно. С другой стороны, если задана система координат, то в ней каждой упорядоченной тройке чисел ставится в соответствие единственная точка. Аффинная система координат на плоскости 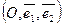 определяет такое же соответствие между точками и упорядоченными парами чисел.
определяет такое же соответствие между точками и упорядоченными парами чисел.
З а д а ч а. Пусть в заданной аффинной системе
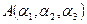
и
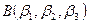
. Требуется найти координаты вектора
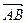
.
Рис. 5
Р е ш е н и е. Из чертежа (рис. 5) видно 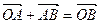 , тогда
, тогда
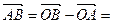
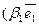 +
+ 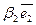 +
+ 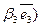
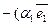 +
+ 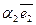 +
+ 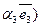 =
=
= 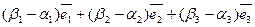 .
.
Таким образом, 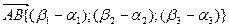 , то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
, то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
Проекция вектора на ось
Ориентированной осью называется прямая, на которой закреплена точка - начало отсчета, выбрана единица длины и направление отсчета.
Рис. 6
Проекцией вектора 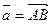 на ось
на ось 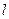
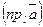 называется величина, численно равная длине отрезка
называется величина, численно равная длине отрезка 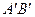 между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от
между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от 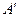 к
к 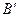 совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.
совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.
Углом между осью и вектором называется угол, 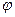 на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что
на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что 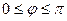 .
.
Свойства проекции вектора на ось.
1.Проекция равна нулю тогда и только тогда, когда вектор перпендикулярен оси (говорят, вектор ортогонален оси).
2. При параллельном переносе вектора его проекция не меняется.
3. Проекция вектора на ось равна произведению длины вектора на
косинус угла между вектором и осью.
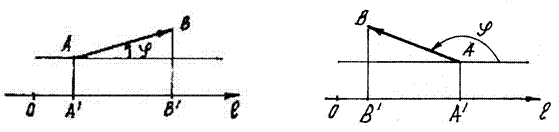
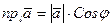 .
.
Рис. 7 Рис. 8
В этой формуле знак проекции регулируется знаком косинуса:
- если 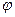 острый угол (рис. 7), то
острый угол (рис. 7), то 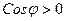 и
и 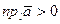 ;
;
- если 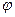 тупой угол (рис. 8), то
тупой угол (рис. 8), то 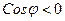 и
и 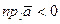 .
.
4. Скалярный множитель можно выносить за знак проекции
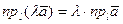 .
.
5. Проекция суммы векторов равна сумме проекций слагаемых
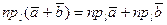 .
.



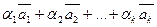 , где
, где  (
(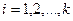 ) – некоторые числа, называется линейной комбинацией данных векторов
) – некоторые числа, называется линейной комбинацией данных векторов 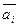 .
. 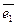 и
и  . Любой компланарный с ними вектор
. Любой компланарный с ними вектор  раскладывается по ним и такое разложение единственно. Т. е.,
раскладывается по ним и такое разложение единственно. Т. е.,  +
+  , где
, где 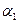 и
и 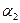 единственные для этого вектора
единственные для этого вектора  вполне определенные числа.
вполне определенные числа. . Любой вектор
. Любой вектор  +
+ 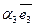 .
. - коэффициентов разложения этого вектора по векторам базиса. С другой стороны, каждой упорядоченной тройке чисел при помощи базиса сопоставляется единственный вектор. Если
- коэффициентов разложения этого вектора по векторам базиса. С другой стороны, каждой упорядоченной тройке чисел при помощи базиса сопоставляется единственный вектор. Если 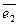 ,
, 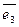 - базис и
- базис и  +
+  . Аналогично дается определение базиса на плоскости, когда вектор имеет две координаты
. Аналогично дается определение базиса на плоскости, когда вектор имеет две координаты 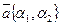 .
. (
( +
+ 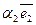 +
+  +
+  +
+ 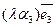 и
и  {
{  ,
, 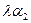 ,
,  }.
}.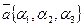 ,
, 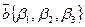 , то
, то  .
.
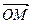 - радиус-вектор точки М. Тогда разложение по векторам базиса
- радиус-вектор точки М. Тогда разложение по векторам базиса 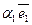 +
+ 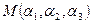 , где
, где 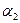 - ордината,
- ордината, 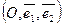 определяет такое же соответствие между точками и упорядоченными парами чисел.
определяет такое же соответствие между точками и упорядоченными парами чисел.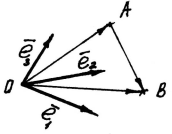
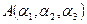 и
и 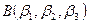 . Требуется найти координаты вектора
. Требуется найти координаты вектора 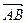 .
.
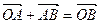 , тогда
, тогда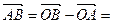
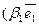 +
+ 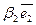 +
+ 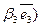
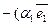 +
+ 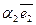 +
+ 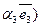 =
=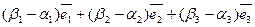 .
.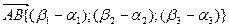 , то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
, то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.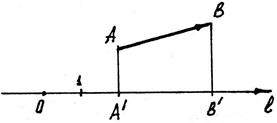
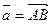 на ось
на ось 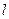
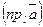 называется величина, численно равная длине отрезка
называется величина, численно равная длине отрезка 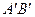 между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от
между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от 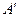 к
к 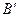 совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.
совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.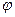 на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что
на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что 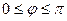 .
.
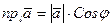 .
.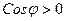 и
и 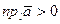 ;
;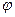 тупой угол (рис. 8), то
тупой угол (рис. 8), то 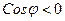 и
и 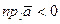 .
.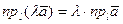 .
.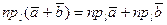 .
.


