Суть методического подхода заключается в поэтапном преобразовании исходных математических моделей движения КА. На первом этапе используется формализм принципа максимума Понтрягина [54]. Составляются гамильтониан и дифференциальные уравнения сопряженных переменных. Далее, путем использования оригинальных преобразований, основывающихся на введении допущений, заменах переменных, алгоритмах понижения порядка систем уравнений, разрабатываются упрощенные модели движения КА и сопряженных переменных. На их основе составляются аналитические зависимости для определения законов оптимального управления и новых соотношений связи. В результате формируются общие условия оптимальности, справедливые для практически любых вариационных задач, относящихся к классу Майера. При этом окончательные решения задач оптимального управления определяются с учетом конкретных исходных данных, граничных условий, ограничений и критериев оптимальности.
Итак, основываясь на формализме принципа максимума Понтрягина [54] запишем гамильтониан:
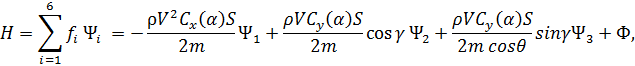
где
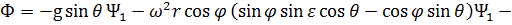
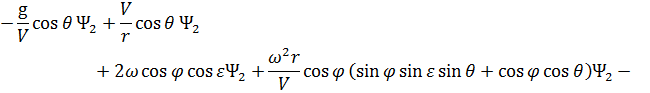
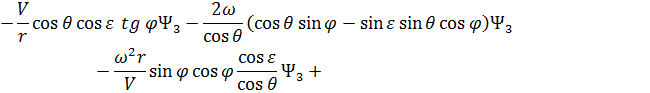
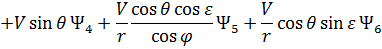
- функция, не зависящая в явном виде от управляющих параметров 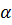 и
и 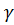 .
.
Сопряженные переменные при движении КА внутри области допустимых значений имеют вид:
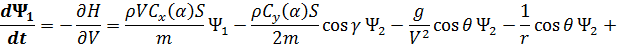
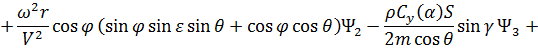
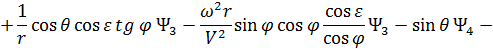
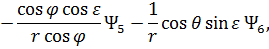
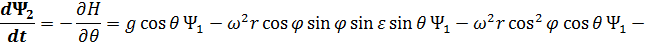
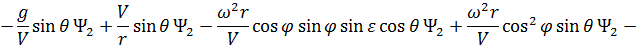
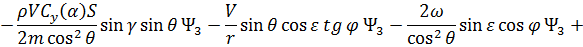
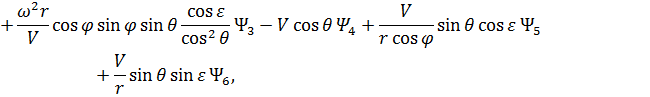


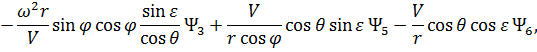
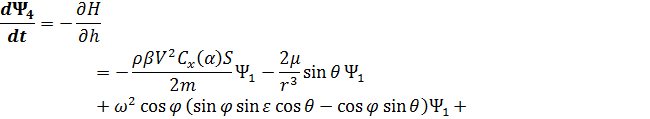
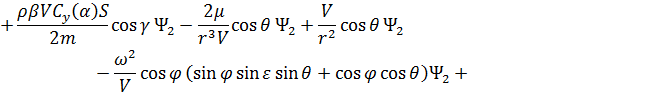

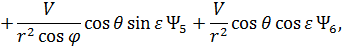

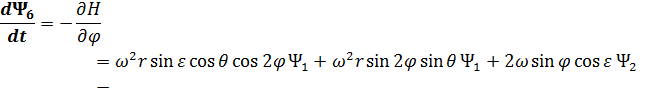
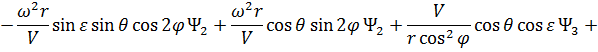
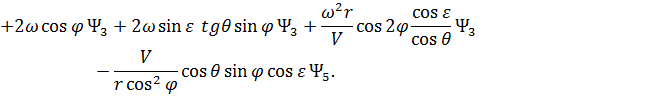
При полете КА по границам допустимой области фазового пространства сопряженные переменные 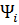 (
(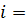 1, 2, …, 6) имеют следующий общий вид [5, 43, 58, 77]:
1, 2, …, 6) имеют следующий общий вид [5, 43, 58, 77]:
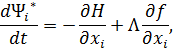
где
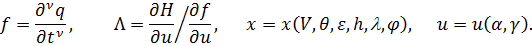
В момент выхода КА на ограничения 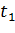 должно быть выполнено условие касания границ области допустимых значений фазового пространства:
должно быть выполнено условие касания границ области допустимых значений фазового пространства:

Сопряженные переменные 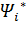 в момент
в момент 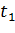 скачком меняют свои значения:
скачком меняют свои значения:
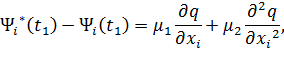
где 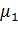 и
и 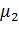 – постоянные.
– постоянные.
Значения 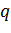 , ν,
, ν, 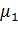 ,
, 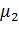 формируются в зависимости от конкретных условий исследуемых вариационных задач.
формируются в зависимости от конкретных условий исследуемых вариационных задач.
Из условия максимума гамильтониана 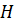 получим формулы для определения законов оптимального управления углами крена и атаки:
получим формулы для определения законов оптимального управления углами крена и атаки:
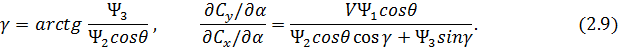
С учетом условия трансверсальности определим значения сопряженных переменных и гамильтониана в конечной точке траектории [43, 58]
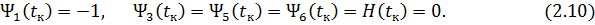
Учитывая, что в правых частях дифференциальных уравнений (2.1) не содержится в явном виде переменная 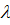 , получим соотношение:
, получим соотношение:
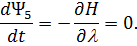
Сопоставляя это соотношение с условием равенства нулю сопряженной переменной 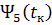 , приходим к выводу о том, что
, приходим к выводу о том, что 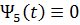 на всем участке полета КА, включая граничные точки траектории:
на всем участке полета КА, включая граничные точки траектории:
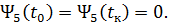
Далее, из условия 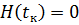 составим дополнительное уравнение, связывающее неизвестные параметры в конечной точке траектории:
составим дополнительное уравнение, связывающее неизвестные параметры в конечной точке траектории:
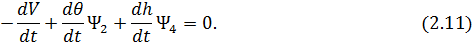
В результате задача определения оптимального управления, обеспечивающего минимум конечной скорости КА, сводится к решению пятипараметрической краевой задачи для дифференциальных уравнений (2.1), (2.7), краевых условий (2.4), (2.5), (2.10), (2.11) и ограничений (2.6).
Как было отмечено выше, решение такого типа задач классическими методами сопряжено со значительными трудностями, в первую очередь, в связи со сложностями определения первого приближения значений сопряженных переменных в граничных точках траектории. Для упрощения поиска структуры оптимального управления КА и расчета траекторий движения аппарата разработан аналитический метод, базирующийся на введении ряда оригинальных преобразований.
При его разработке использовались общеизвестные допущения, обоснованные в ряде работ [26, 58, 79, 81, 84, 85]
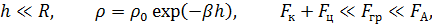
где 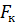 ,
, 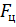 ,
, 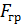 ,
, 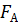 - кориолисова, центробежная, гравитационная и аэродинамическая силы соответственно,
- кориолисова, центробежная, гравитационная и аэродинамическая силы соответственно, 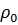 – плотность атмосферы на поверхности планеты,
– плотность атмосферы на поверхности планеты, 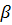 – логарифмический коэффициент изменения плотности атмосферы от высоты.
– логарифмический коэффициент изменения плотности атмосферы от высоты.
В результате система (2.1) перепишется в виде:
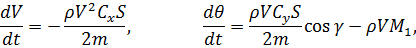
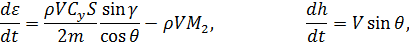
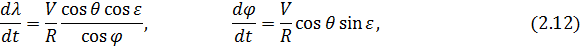

Следуя [26, 58, 63], будем считать 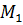 и
и 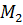 – кусочно-постоянными функциями.
– кусочно-постоянными функциями.
Введем замены переменных
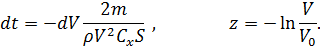
Это позволит упростить анализ уравнений движения КА и сопряженных переменных и определить структуру оптимального управления.
В результате получим систему, не содержащую в явном виде аргумент 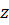 :
:
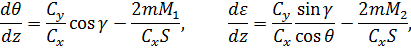
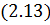
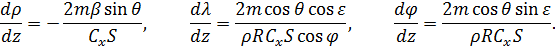
Отметим, что при движении КА в атмосфере аргумент 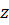 возрастает.
возрастает.
Для определения оптимальных законов управления параметрами 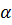 и
и 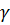 также воспользуемся принципом максимума Понтрягина [54]. При
также воспользуемся принципом максимума Понтрягина [54]. При 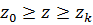 гамильтониан и система уравнений сопряженных переменных при движении КА внутри допустимой области фазовых координат запишутся следующим образом:
гамильтониан и система уравнений сопряженных переменных при движении КА внутри допустимой области фазовых координат запишутся следующим образом:
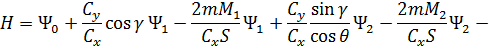
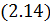
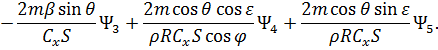
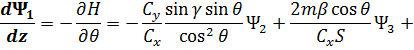
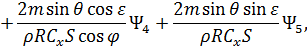
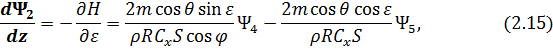
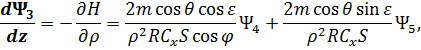
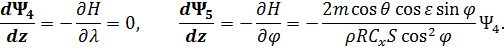
Сопряженные переменные при анализе оптимальных траекторий, проходящих по границам области фазовых координат 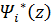 (
(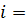 1, 2, …, 5), а также законы управления при полете КА по изоучасткам определяются в зависимости от вида заданных ограничений и будут рассмотрены при исследовании конкретных вариационных задач.
1, 2, …, 5), а также законы управления при полете КА по изоучасткам определяются в зависимости от вида заданных ограничений и будут рассмотрены при исследовании конкретных вариационных задач.
При использовании в качестве аргумента параметра 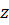 , согласно [43], в систему (2.13) вводится дополнительное дифференциальное уравнение
, согласно [43], в систему (2.13) вводится дополнительное дифференциальное уравнение 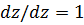 . В связи с тем, что правые части этой системы не содержат в явном виде аргумент
. В связи с тем, что правые части этой системы не содержат в явном виде аргумент 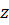 , соответствующее уравнение для сопряженной переменной
, соответствующее уравнение для сопряженной переменной 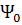 определяется формулой
определяется формулой 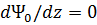 .
.
Согласно сделанному предположению, в уравнения (2.13)-(2.15) входят кусочно-постоянные разрывные функции 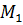 ,
, 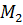 . Однако в силу теоремы Вейерштрасса-Эрдмана [43] наличие разрывов в правых частях уравнений не нарушает непрерывности гамильтониана и сопряженных переменных:
. Однако в силу теоремы Вейерштрасса-Эрдмана [43] наличие разрывов в правых частях уравнений не нарушает непрерывности гамильтониана и сопряженных переменных:

где 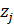 – значение аргумента, соответствующее j -му моменту разрыва функций
– значение аргумента, соответствующее j -му моменту разрыва функций 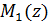 или
или 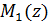 ,
, 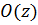 – величина меньшего порядка, чем
– величина меньшего порядка, чем 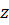 .
.
Законы изменения 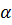 и
и 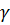 при оптимальном управлении определяются в результате решения уравнений
при оптимальном управлении определяются в результате решения уравнений 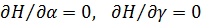 и их можно записать в виде
и их можно записать в виде
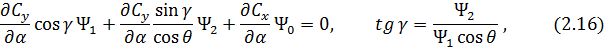
Граничные условия для сопряженных переменных 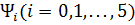 при
при 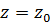 и
и 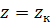 получим из условия трансверсальности [43]
получим из условия трансверсальности [43]
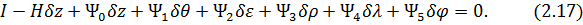
Таким образом, для определения оптимальных законов изменения управляющих параметров 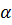 и
и 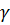 необходимо решить уравнения (2.16) с учетом дифференциальных связей (2.13)-(2.15) и краевых условий (2.17).
необходимо решить уравнения (2.16) с учетом дифференциальных связей (2.13)-(2.15) и краевых условий (2.17).
В рамках предложенного метода применительно к исследуемым задачам оптимального управления КА в атмосфере можно записать общие формулы для определения сопряженных переменных 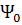 и
и 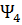 :
:

В связи с тем, что гамильтониан 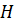 в явном виде не зависит от аргумента
в явном виде не зависит от аргумента 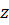 , справедливо соотношение
, справедливо соотношение
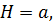
что позволяет записать дополнительное уравнение связи между неизвестными параметрами движения КА и сопряженными переменными:
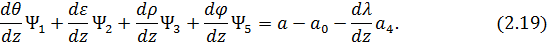
Разработанные соотношения (2.16), (2.18), (2.19) являются универсальными и представляют собой теоретическую основу для исследования практически любых задач оптимального управления, относящихся к классу Майера. Вместе с тем, этих соотношений недостаточно для окончательного расчета оптимальных траекторий. Для этого необходимо получение всех (в том числе и не определяемых по разработанным универсальным соотношениям) граничных значений фазовых координат и сопряженных переменных. Эти неизвестные параметры, в том числе переменные 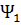 и
и 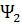 , в явном виде влияющие на законы оптимального управления КА (2.16), определяются в зависимости от условий конкретных вариационных задач. Окончательные решенияконкретных вариационных задач будут представлены в последующих разделах.
, в явном виде влияющие на законы оптимального управления КА (2.16), определяются в зависимости от условий конкретных вариационных задач. Окончательные решенияконкретных вариационных задач будут представлены в последующих разделах.



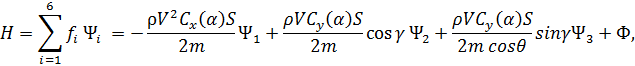
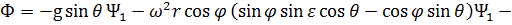
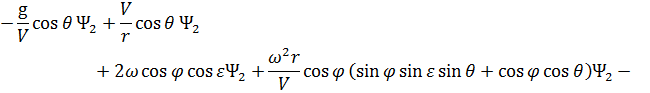
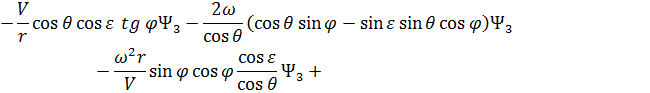
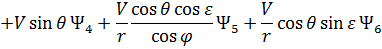
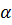 и
и 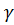 .
.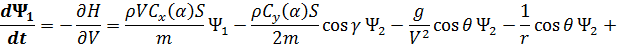
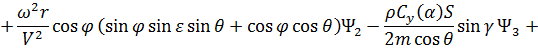
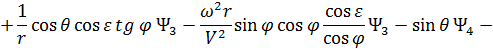
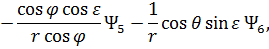
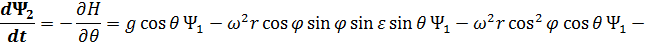
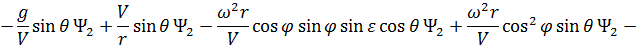
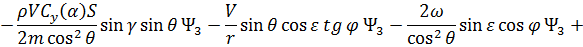
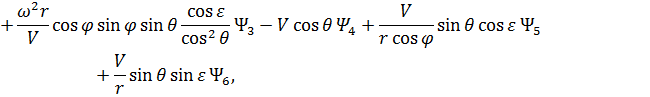


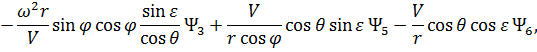
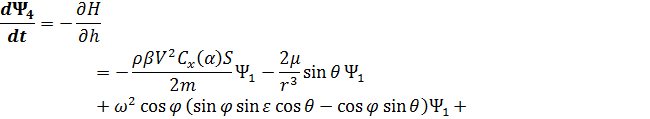
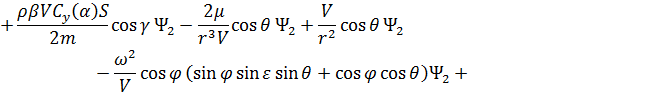

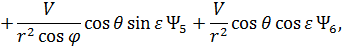

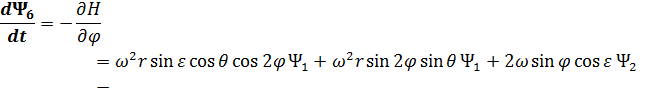
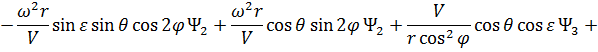
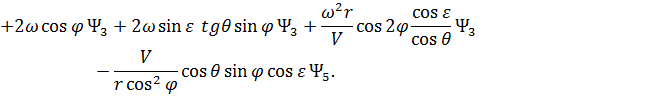
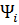 (
(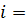 1, 2, …, 6) имеют следующий общий вид [5, 43, 58, 77]:
1, 2, …, 6) имеют следующий общий вид [5, 43, 58, 77]: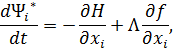
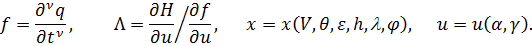
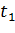 должно быть выполнено условие касания границ области допустимых значений фазового пространства:
должно быть выполнено условие касания границ области допустимых значений фазового пространства:
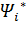 в момент
в момент 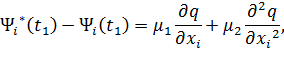
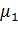 и
и 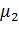 – постоянные.
– постоянные.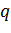 , ν,
, ν, 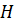 получим формулы для определения законов оптимального управления углами крена и атаки:
получим формулы для определения законов оптимального управления углами крена и атаки: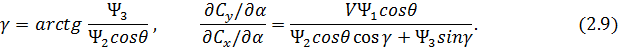
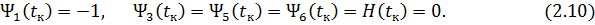
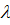 , получим соотношение:
, получим соотношение: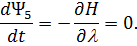
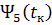 , приходим к выводу о том, что
, приходим к выводу о том, что 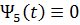 на всем участке полета КА, включая граничные точки траектории:
на всем участке полета КА, включая граничные точки траектории: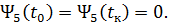
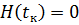 составим дополнительное уравнение, связывающее неизвестные параметры в конечной точке траектории:
составим дополнительное уравнение, связывающее неизвестные параметры в конечной точке траектории: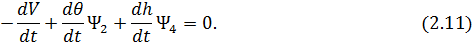
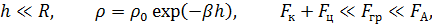
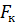 ,
, 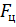 ,
, 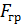 ,
, 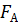 - кориолисова, центробежная, гравитационная и аэродинамическая силы соответственно,
- кориолисова, центробежная, гравитационная и аэродинамическая силы соответственно, 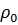 – плотность атмосферы на поверхности планеты,
– плотность атмосферы на поверхности планеты, 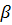 – логарифмический коэффициент изменения плотности атмосферы от высоты.
– логарифмический коэффициент изменения плотности атмосферы от высоты.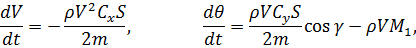
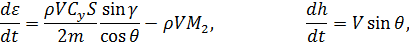
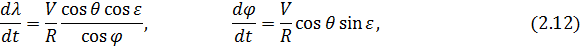

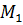 и
и 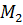 – кусочно-постоянными функциями.
– кусочно-постоянными функциями.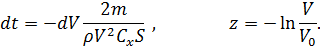
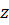 :
: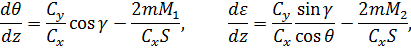
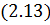
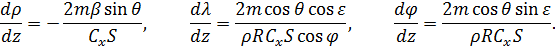
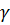 также воспользуемся принципом максимума Понтрягина [54]. При
также воспользуемся принципом максимума Понтрягина [54]. При 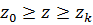 гамильтониан и система уравнений сопряженных переменных при движении КА внутри допустимой области фазовых координат запишутся следующим образом:
гамильтониан и система уравнений сопряженных переменных при движении КА внутри допустимой области фазовых координат запишутся следующим образом: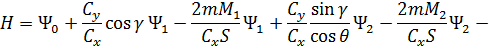
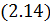
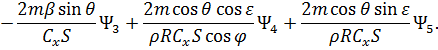
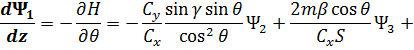
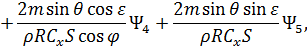
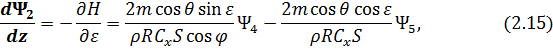
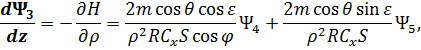
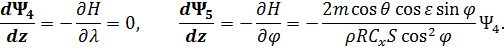
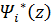 (
(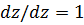 . В связи с тем, что правые части этой системы не содержат в явном виде аргумент
. В связи с тем, что правые части этой системы не содержат в явном виде аргумент 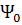 определяется формулой
определяется формулой 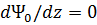 .
.
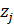 – значение аргумента, соответствующее j -му моменту разрыва функций
– значение аргумента, соответствующее j -му моменту разрыва функций 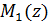 или
или 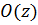 – величина меньшего порядка, чем
– величина меньшего порядка, чем 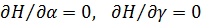 и их можно записать в виде
и их можно записать в виде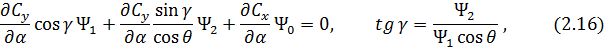
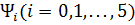 при
при 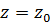 и
и 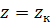 получим из условия трансверсальности [43]
получим из условия трансверсальности [43]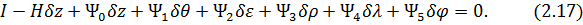
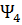 :
:
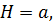
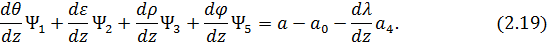
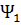 и
и 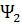 , в явном виде влияющие на законы оптимального управления КА (2.16), определяются в зависимости от условий конкретных вариационных задач. Окончательные решенияконкретных вариационных задач будут представлены в последующих разделах.
, в явном виде влияющие на законы оптимального управления КА (2.16), определяются в зависимости от условий конкретных вариационных задач. Окончательные решенияконкретных вариационных задач будут представлены в последующих разделах.


