Линейная парная регрессионная модель имеет вид: 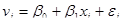 , i=1, 2,…,n. Основные предпосылки регрессионного анализа состоя в следующем:
, i=1, 2,…,n. Основные предпосылки регрессионного анализа состоя в следующем:
· зависимая переменная 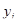 (возмущение
(возмущение 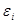 ) является случайной величиной, а объясняющая переменная
) является случайной величиной, а объясняющая переменная 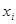 — неслучайной;
— неслучайной;
· математическое ожидание возмущения 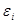 равно нулю
равно нулю 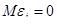 ;
;
· дисперсия зависимой переменной 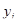 (возмущения
(возмущения 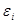 ) постоянна (для всех i) и равна
) постоянна (для всех i) и равна 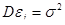 ;
;
· переменные  и
и 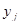 (возмущения
(возмущения 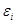 и
и 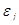 ) не коррелированы
) не коррелированы  ;
;
· зависимая переменная 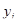 (возмущение
(возмущение 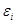 ) является нормально распределенной случайной величиной.
) является нормально распределенной случайной величиной.
Оценка параметров двумерной регрессионной модели
Предположим, что для оценки неизвестных параметров 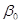 и
и 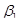 , уравнения регрессии
, уравнения регрессии 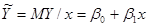 из двумерной генеральной совокупности взята выборка объемом n, где (
из двумерной генеральной совокупности взята выборка объемом n, где (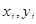 ) — результат i-го наблюдения
) — результат i-го наблюдения 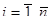 .
.
Согласно методу наименьших квадратов, в качестве оценок неизвестных параметров 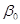 и
и 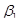 , следует брать такие значения выборочных характеристик
, следует брать такие значения выборочных характеристик 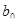 и
и 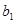 , которые минимизируют сумму квадратов отклонений наблюдаемых значений зависимой переменной от оцененных значений, т. е.
, которые минимизируют сумму квадратов отклонений наблюдаемых значений зависимой переменной от оцененных значений, т. е. 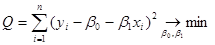 .
.
Дифференцируя Q по 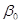 и
и 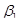 , и приравнивая производные нулю,
, и приравнивая производные нулю, 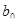 и
и 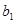 , получаем систему нормальных уравнений, решая которую относительно получаем:
, получаем систему нормальных уравнений, решая которую относительно получаем:
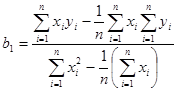 ; (2.90)
; (2.90)
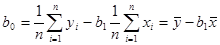 . (2.91)
. (2.91)
Если перейти к центрированным величинам 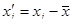 , для которых
, для которых 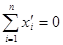 , то выражения для коэффициентов уравнения регрессии существенно упрощаются:
, то выражения для коэффициентов уравнения регрессии существенно упрощаются:
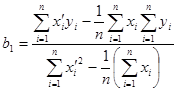 ;
; 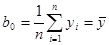 . (2.92)
. (2.92)
Коэффициент 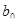 определяет точку пересечения линии регрессии с осью OY и представляет собой среднее значение зависимой переменной в точке х=0. Коэффициент
определяет точку пересечения линии регрессии с осью OY и представляет собой среднее значение зависимой переменной в точке х=0. Коэффициент 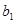 характеризует угол наклона линии регрессии к оси ОХ и показывает среднюю величину изменения зависимой переменной при увеличении объясняющей переменной на единицу своего измерения.
характеризует угол наклона линии регрессии к оси ОХ и показывает среднюю величину изменения зависимой переменной при увеличении объясняющей переменной на единицу своего измерения.
Размерность коэффициента 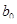 совпадает с размерностью объясняемой переменной. Размерность коэффициента
совпадает с размерностью объясняемой переменной. Размерность коэффициента 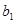 равна отношению размерностей зависимой и объясняющей переменных.
равна отношению размерностей зависимой и объясняющей переменных.

На основе оцененного уравнения регрессии можно получить расчетные значения 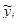 , т. е. значения
, т. е. значения 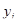 при заданной величине объясняющей переменной, в предположении, что последняя является единственной причиной изменения зависимой переменной, а ошибка оценки равна нулю. Разброс
при заданной величине объясняющей переменной, в предположении, что последняя является единственной причиной изменения зависимой переменной, а ошибка оценки равна нулю. Разброс  вокруг
вокруг 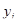 обусловлен воздействием случайных факторов. Количественная оценка величины ошибки определяется на основе остатка
обусловлен воздействием случайных факторов. Количественная оценка величины ошибки определяется на основе остатка 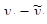 .
.
Для полной спецификации линейной парной регрессионной модели необходимо построить оценки не только коэффициентов регрессии, но и дисперсии  .
.
Оценка остаточной дисперсии имеет вид:
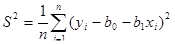 , (2.93)
, (2.93)
а несмещенная оценка остаточной дисперсии:
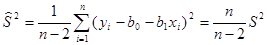 . (2.94)
. (2.94)
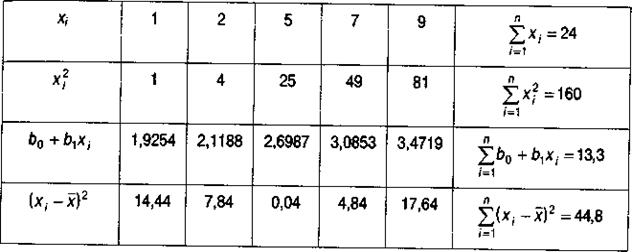
Пример 13.1. Измерение некоторой величины Y зависимости от значения аргумента Х дали результаты, приведенные в таблице:

Считая, что генеральное уравнение регрессии – линейное  , требуется определить:
, требуется определить:
а) точечные оценки 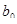 и
и 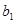 параметров уравнения;
параметров уравнения;
б) оценку остаточной дисперсии 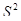 ;
;
в) оценки дисперсий  выборочных характеристик
выборочных характеристик 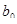 и
и 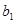 ;
;
г) точечную оценку при 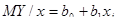 х=6.
х=6.
Решение.
А. В регрессионном анализе в случае рассмотрения линейного уравнения регрессии оценка параметров уравнения осуществляется по формулам:
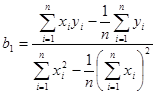 ,
,  .
.
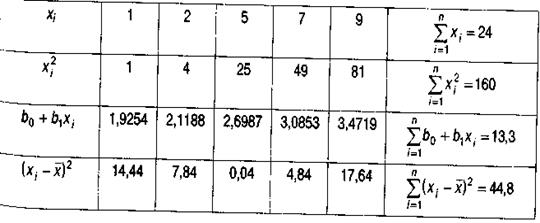
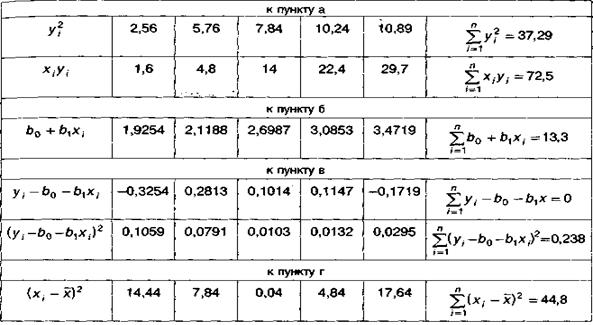
Для получения точечных оценок составим вспомогательную таблицу:
На основе данных таблицы:
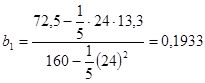 ,
,  .
.
Б. Оценка  остаточной дисперсии
остаточной дисперсии  относительно линии регрессии имеет вид:
относительно линии регрессии имеет вид:
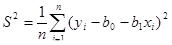 .
.
Воспользовавшись оценками параметров уравнения, найденных в пункте а), и результатами расчетов, представленных во вспомогательной таблице, получим:
 .
.
В. Оценки дисперсии 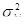 выборочных характеристик
выборочных характеристик 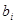 i=0,1 рассчитываются как:
i=0,1 рассчитываются как:
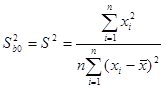 ;
; 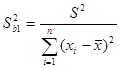 , где
, где 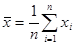 .
.
На основе данных вспомогательной таблицы и результатов остаточной дисперсии  , полученной в пункте б) получим:
, полученной в пункте б) получим:
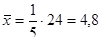
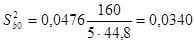 ;
;  .
.
Г. Воспользовавшись результатами расчетов пункта а) запишем оценку уравнения регрессии: 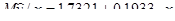 . Тогда оценка условного математического ожидания y при x=6 составит:
. Тогда оценка условного математического ожидания y при x=6 составит:
 .
.
Пример 13.2. Измерение некоторой величины Y в зависимости от значения аргумента Х дали результаты, приведенные в таблице:
Считая, что генеральное уравнение регрессии имеет вид гиперболической функции 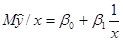 требуется определить точечные оценки
требуется определить точечные оценки 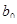 и
и 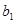 параметров уравнения.
параметров уравнения.
Решение.
В случае, когда вид предполагаемого уравнения регрессии отличается от линейного, на первом этапе регрессионного анализа осуществляют преобразование исходного уравнения, сводящее его к линейному. В случае гиперболической зависимости вида 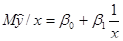 преобразование состоит в замене переменных
преобразование состоит в замене переменных 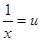 .
.
Построим вспомогательную таблицу:
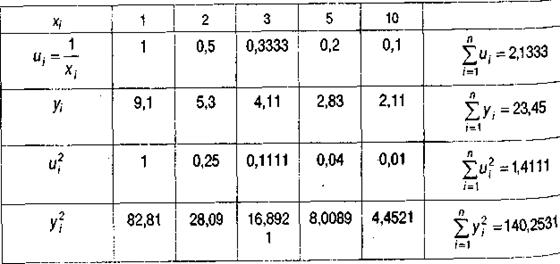
На основе данных таблицы параметров уравнения имеет вид:
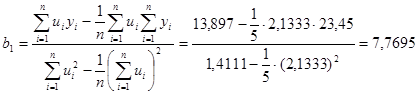 ;
;
 .
.
В итоге оценка уравнения регрессии: 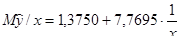 .
.
Проверка значимости уравнения регрессии
Так как выборочные характеристики являются случайными величинами, то в регрессионном анализе решаются задачи проверки значимости уравнения регрессии и интервального оценивания параметров 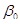 ,
,  ,
, 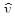 и
и  .
.
Для проверки значимости уравнения регрессии, т. е. гипотезы  :
: 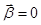 , используют критерий, основанный на статистике
, используют критерий, основанный на статистике
 , (2.95)
, (2.95)
которая при истинности гипотезы Н0 имеет F-распределение с числом степеней свободы v1=1 — числителя и v2=n-2 — знаменателя, где QR и Qост — суммы квадратов отклонений, обусловленных соответственно регрессией и остаточными, не включенными в модель факторами, — определяются в соответствии с формулами:
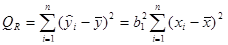 ; (2.96)
; (2.96)
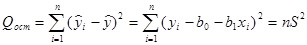 . (2.97)
. (2.97)
Гипотеза  :
: 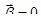 отвергается и уравнение регрессии считается значимым, если наблюдаемое значение статистики оказывается больше критического значения Fнабл>Fкр, найденного для уровня значимости
отвергается и уравнение регрессии считается значимым, если наблюдаемое значение статистики оказывается больше критического значения Fнабл>Fкр, найденного для уровня значимости  и числа степеней свободы v1=1 — числителя и v2=n-2 — знаменателя: Fкр(
и числа степеней свободы v1=1 — числителя и v2=n-2 — знаменателя: Fкр( ; v1В противном случае гипотеза не отвергается.
; v1В противном случае гипотеза не отвергается.
В случае значимого уравнения регрессии необходимо проверить значимость отдельных его коэффициентов.
Проверка значимости отдельных коэффициентов регрессии
Проверка значимости коэффициента регрессии  сводится к проверке гипотезы
сводится к проверке гипотезы 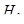 :
:  . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики
 , (2.98)
, (2.98)
которая при истинности гипотезы 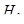 имеет t-распределение с числом степеней свободы v2=n-2.
имеет t-распределение с числом степеней свободы v2=n-2.
Несмещенная оценка среднего квадратического отклонения равна:
 ,
,
где 
откуда  (2.99)
(2.99)
Гипотеза 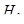 :
: 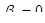 отвергается и коэффициент регрессии считается значимым, если наблюдаемое значение статистики по модулю оказывается больше критического значения
отвергается и коэффициент регрессии считается значимым, если наблюдаемое значение статистики по модулю оказывается больше критического значения 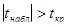 , найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St(
, найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St( ;v). В противном случае гипотеза не отвергается.
;v). В противном случае гипотеза не отвергается.
Проверка значимости коэффициента регрессии 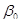 сводится к проверке гипотезы
сводится к проверке гипотезы 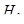 :
:  . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики
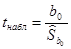 , (2.100)
, (2.100)
которая при истинности гипотезы 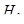 имеет t-распределение с числом степеней свободы v=n-2.
имеет t-распределение с числом степеней свободы v=n-2.
Несмещенная оценка среднего квадратического отклонения равна:
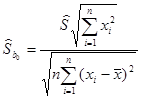 ,
,
откуда 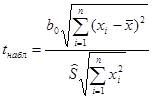 (2.101)
(2.101)
Гипотеза 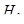 :
:  отвергается, если наблюдаемое значение статистики по модулю оказывается больше критического значения
отвергается, если наблюдаемое значение статистики по модулю оказывается больше критического значения  , найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St(
, найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St( ;v). В противном случае гипотеза не отвергается.
;v). В противном случае гипотеза не отвергается.
Пример 13.3. При анализе зависимости некоторой величины у от значения аргумента х, принимающей значения 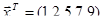 были получены точечные оценки
были получены точечные оценки 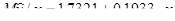 и S2=0?0476. Требуется:
и S2=0?0476. Требуется:
а) на уровне значимости 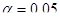 проверить значимость уравнения регрессии;
проверить значимость уравнения регрессии;
б) проверить значимость коэффициента регрессии  при
при 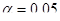 ;
;
в) проверить значимость коэффициента регрессии 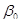 при
при 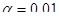 .
.
Решение.
А. Проверка значимости уравнения регрессии сводится к проверке гипотезы  :
:  . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики 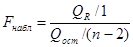 .
.
Рассчитываем наблюдаемое значение статистики:
В случае, когда вид уравнения регрессии отличается от линейного, расчеты должны производиться для преобразованной переменной (например, в случае гиперболического уравнения для 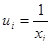 ).
).
На основании расчетов, представленных в таблице:
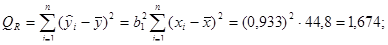 ;
;
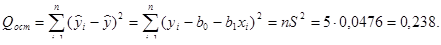 .
.
Таким образом, 
По таблицам F-распределения найдем критическое значение F-статистики для уровня значимости 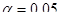 и числа степеней свободы v1=1 – числителя и v2=5-2=3 –знаменателя:
и числа степеней свободы v1=1 – числителя и v2=5-2=3 –знаменателя: 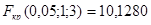 . Так как наблюдаемое значение F-статистики больше критического значения, то гипотеза о незначимости уравнения регрессии отвергается с вероятностью ошибки, равной 0,05. Следовательно, уравнение регрессии значимо.
. Так как наблюдаемое значение F-статистики больше критического значения, то гипотеза о незначимости уравнения регрессии отвергается с вероятностью ошибки, равной 0,05. Следовательно, уравнение регрессии значимо.
Б. Проверка значимости коэффициента регрессии  сводится к проверке гипотезы
сводится к проверке гипотезы  :
: 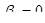 . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики 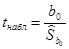 , которая при истинности гипотезы
, которая при истинности гипотезы  имеет t-распределение с числом степеней свободы v=n-2. Несмещенная оценка среднего квадратического отклонения равна:
имеет t-распределение с числом степеней свободы v=n-2. Несмещенная оценка среднего квадратического отклонения равна:
 ,
,
откуда 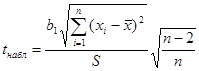 .
.
Для расчета наблюдаемого значения статистики воспользуемся результатами расчетов, представленных в таблице пункта а):  .
.
По таблицам t-распределения найдем критическое значение t-статистики для уровня значимости 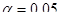 и числа степеней свободы v=5-2=3:
и числа степеней свободы v=5-2=3: 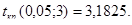 Так как наблюдаемое значение t-статистики больше критического значения, то гипотеза о равенстве коэффициента регрессии
Так как наблюдаемое значение t-статистики больше критического значения, то гипотеза о равенстве коэффициента регрессии  нулю отвергается с вероятностью ошибки, равной 0,05.
нулю отвергается с вероятностью ошибки, равной 0,05.
В. Проверка значимости коэффициента регрессии  сводится к проверке гипотезы
сводится к проверке гипотезы 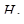 :
: 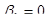 . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики  , которая при истинности гипотезы
, которая при истинности гипотезы  имеет t-распределение с числом степеней свободы v=n-2. Несмещенная оценка среднего квадратического отклонения равна
имеет t-распределение с числом степеней свободы v=n-2. Несмещенная оценка среднего квадратического отклонения равна
 , откуда
, откуда 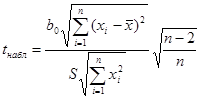 .
.
Для расчета наблюдаемого значения статистики воспользуемся результатами расчетов, представленных в таблице пункта а):  .
.
По таблицам t-распределения найдем критическое значение t-статистики для уровня значимости  и числа степеней свободы v=5-2=3:
и числа степеней свободы v=5-2=3:  . Так как наблюдаемое значение t-статистики по модулю больше критического значения, то гипотеза о равенстве коэффициента регрессии
. Так как наблюдаемое значение t-статистики по модулю больше критического значения, то гипотеза о равенстве коэффициента регрессии  нулю отвергается с вероятностью ошибки, равной 0,01.
нулю отвергается с вероятностью ошибки, равной 0,01.
Интервальные оценки параметров регрессии
Если гипотеза 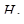 :
: 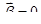 отвергается, то представляет интерес определение с надежностью
отвергается, то представляет интерес определение с надежностью  интервальных оценок параметров регрессии. При построении доверительных интервалов исходят из распределения соответствующих статистик. Интервальные оценки имеют вид:
интервальных оценок параметров регрессии. При построении доверительных интервалов исходят из распределения соответствующих статистик. Интервальные оценки имеют вид:
· коэффициента регрессии 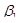 :
:
 ; (2.102)
; (2.102)
· свободного члена уравнения регрессии  :
:
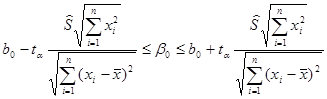 ; (2.103)
; (2.103)
· условного математического ожидания при х=х0:
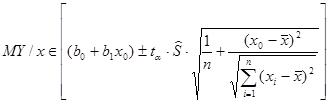 ; (2.104)
; (2.104)
· интервала предсказания в точке х=хn+1:
 . (2.105)
. (2.105)
В формулах (2.102-2.105):
 – выборочная оценка несмещенного остаточного среднего квадратического отклонения;
– выборочная оценка несмещенного остаточного среднего квадратического отклонения;
 определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы v=n-2. При больших объемах выборки (по крайней мере, n>30) можно пользоваться табл. 1 Приложений нормального закона распределения.
и числа степеней свободы v=n-2. При больших объемах выборки (по крайней мере, n>30) можно пользоваться табл. 1 Приложений нормального закона распределения.
Пример 13.4. По данным примера 13.3. требуется:
а) найти длину доверительного интервала генерального коэффициента регрессии  с надежностью
с надежностью 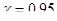 ;
;
б) найти нижнюю границу интервальной оценки для генерального коэффициента регрессии 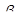 с надежностью
с надежностью 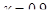 ;
;
в) с надежностью 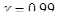 построить интервальную оценку условного математического ожидания My|x при х0=6;
построить интервальную оценку условного математического ожидания My|x при х0=6;
г) с надежностью 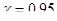 определить верхнюю границу интервала предсказания при х0=10.
определить верхнюю границу интервала предсказания при х0=10.
Решение.
А. При построении интервальной оценки коэффициента регрессии  исходят из того, что статистика
исходят из того, что статистика 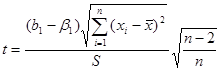 имеет t-распределение с числом степеней свободы v=n-2. Из этого следует, что генеральный коэффициент регрессии
имеет t-распределение с числом степеней свободы v=n-2. Из этого следует, что генеральный коэффициент регрессии  с надежностью
с надежностью 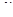 будет находиться внутри интервала, определяемого формулой:
будет находиться внутри интервала, определяемого формулой:
 ,
,
где  определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы v=n-2. Длина доверительного интервала составит:
и числа степеней свободы v=n-2. Длина доверительного интервала составит:
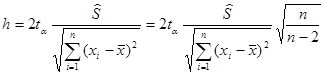 .
.
По таблицам распределения Стьюдента 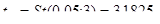 Воспользовавшись данными вспомогательной таблицы, получим:
Воспользовавшись данными вспомогательной таблицы, получим: 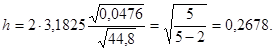
Б. Нижнюю границу интервальной оценки для коэффициента регрессии 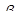 определим по формуле
определим по формуле
 ,
,
где  определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости 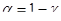 и числа степеней свободы v=n-2.
и числа степеней свободы v=n-2.
По таблицам распределения Стьюдента 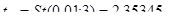 На основе расчетов, представленных во вспомогательной таблице, получим:
На основе расчетов, представленных во вспомогательной таблице, получим:
 .
.
В. Интервальная оценкаусловного математического ожидания 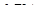 равна
равна
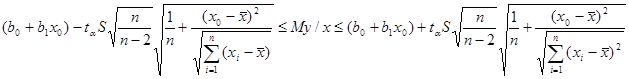 где
где  определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости 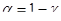 и числа степеней свободы v=n-2.
и числа степеней свободы v=n-2.
По таблицам распределения Стьюдента 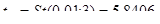 Воспользовавшись данными вспомогательной таблицы при х0=6, получим:
Воспользовавшись данными вспомогательной таблицы при х0=6, получим:
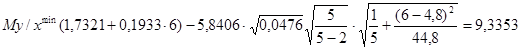 ;
;
 .
.
Таким образом, с надежностью 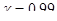 условное математическое ожидание My|х=6 будет лежать в пределах:
условное математическое ожидание My|х=6 будет лежать в пределах: 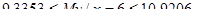
Г. Верхнюю границу интервала предсказания при х0=10 определим по формуле:
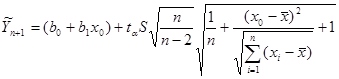 ,
,
где  определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости 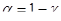 и числа степеней свободы v=n-2.
и числа степеней свободы v=n-2.
По таблицам распределения Стьюдента 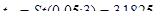 На основе расчетов, представленных во вспомогательной таблице, при х0=10, получим:
На основе расчетов, представленных во вспомогательной таблице, при х0=10, получим:

Основные формулы, используемые при проверке значимости в регрессионном анализе 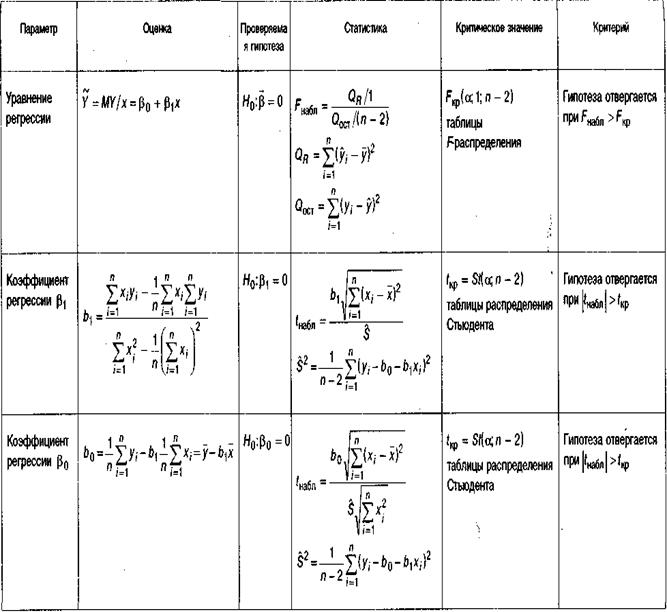



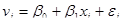 , i=1, 2,…,n. Основные предпосылки регрессионного анализа состоя в следующем:
, i=1, 2,…,n. Основные предпосылки регрессионного анализа состоя в следующем: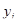 (возмущение
(возмущение 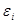 ) является случайной величиной, а объясняющая переменная
) является случайной величиной, а объясняющая переменная 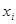 — неслучайной;
— неслучайной;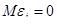 ;
;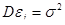 ;
; и
и 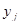 (возмущения
(возмущения 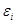 и
и 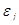 ) не коррелированы
) не коррелированы  ;
;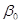 и
и 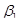 , уравнения регрессии
, уравнения регрессии 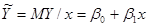 из двумерной генеральной совокупности взята выборка объемом n, где (
из двумерной генеральной совокупности взята выборка объемом n, где (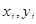 ) — результат i-го наблюдения
) — результат i-го наблюдения 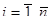 .
.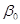 и
и 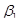 , следует брать такие значения выборочных характеристик
, следует брать такие значения выборочных характеристик 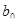 и
и 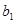 , которые минимизируют сумму квадратов отклонений наблюдаемых значений зависимой переменной от оцененных значений, т. е.
, которые минимизируют сумму квадратов отклонений наблюдаемых значений зависимой переменной от оцененных значений, т. е. 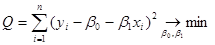 .
.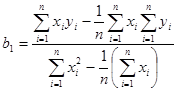 ; (2.90)
; (2.90)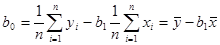 . (2.91)
. (2.91)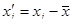 , для которых
, для которых 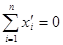 , то выражения для коэффициентов уравнения регрессии существенно упрощаются:
, то выражения для коэффициентов уравнения регрессии существенно упрощаются: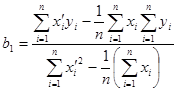 ;
; 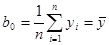 . (2.92)
. (2.92)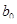 совпадает с размерностью объясняемой переменной. Размерность коэффициента
совпадает с размерностью объясняемой переменной. Размерность коэффициента 
 , т. е. значения
, т. е. значения  вокруг
вокруг 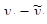 .
. .
.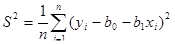 , (2.93)
, (2.93)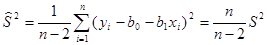 . (2.94)
. (2.94)
 , требуется определить:
, требуется определить: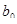 и
и 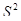 ;
; выборочных характеристик
выборочных характеристик 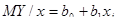 х=6.
х=6.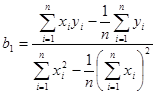 ,
,  .
.

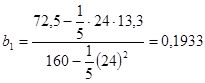 ,
,  .
. остаточной дисперсии
остаточной дисперсии  относительно линии регрессии имеет вид:
относительно линии регрессии имеет вид: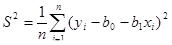 .
. .
.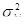 выборочных характеристик
выборочных характеристик 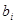 i=0,1 рассчитываются как:
i=0,1 рассчитываются как: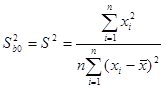 ;
; 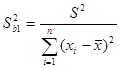 , где
, где 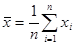 .
.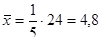
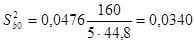 ;
;  .
.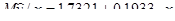 . Тогда оценка условного математического ожидания y при x=6 составит:
. Тогда оценка условного математического ожидания y при x=6 составит: .
.
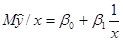 требуется определить точечные оценки
требуется определить точечные оценки 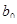 и
и 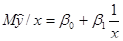 преобразование состоит в замене переменных
преобразование состоит в замене переменных 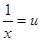 .
.

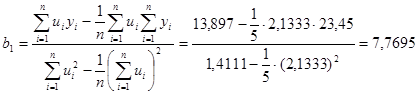 ;
; .
.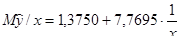 .
.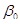 ,
,  ,
, 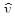 и
и  .
. :
: 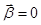 , используют критерий, основанный на статистике
, используют критерий, основанный на статистике , (2.95)
, (2.95)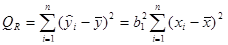 ; (2.96)
; (2.96)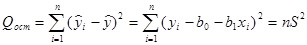 . (2.97)
. (2.97)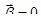 отвергается и уравнение регрессии считается значимым, если наблюдаемое значение статистики оказывается больше критического значения Fнабл>Fкр, найденного для уровня значимости
отвергается и уравнение регрессии считается значимым, если наблюдаемое значение статистики оказывается больше критического значения Fнабл>Fкр, найденного для уровня значимости  и числа степеней свободы v1=1 — числителя и v2=n-2 — знаменателя: Fкр(
и числа степеней свободы v1=1 — числителя и v2=n-2 — знаменателя: Fкр(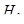 :
:  . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики , (2.98)
, (2.98) ,
,
 (2.99)
(2.99)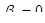 отвергается и коэффициент регрессии считается значимым, если наблюдаемое значение статистики по модулю оказывается больше критического значения
отвергается и коэффициент регрессии считается значимым, если наблюдаемое значение статистики по модулю оказывается больше критического значения 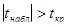 , найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St(
, найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St(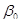 сводится к проверке гипотезы
сводится к проверке гипотезы 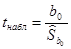 , (2.100)
, (2.100)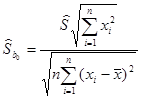 ,
,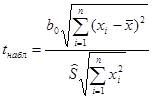 (2.101)
(2.101) , найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St(
, найденного для уровня значимости а и числа степеней свободы v2=n-2:tкр=St(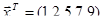 были получены точечные оценки
были получены точечные оценки 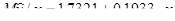 и S2=0?0476. Требуется:
и S2=0?0476. Требуется: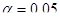 проверить значимость уравнения регрессии;
проверить значимость уравнения регрессии; при
при 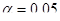 ;
;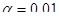 .
. :
:  . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики 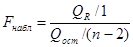 .
.
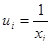 ).
).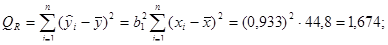 ;
;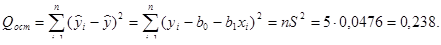 .
.
 и числа степеней свободы v1=1 – числителя и v2=5-2=3 –знаменателя:
и числа степеней свободы v1=1 – числителя и v2=5-2=3 –знаменателя: 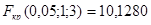 . Так как наблюдаемое значение F-статистики больше критического значения, то гипотеза о незначимости уравнения регрессии отвергается с вероятностью ошибки, равной 0,05. Следовательно, уравнение регрессии значимо.
. Так как наблюдаемое значение F-статистики больше критического значения, то гипотеза о незначимости уравнения регрессии отвергается с вероятностью ошибки, равной 0,05. Следовательно, уравнение регрессии значимо.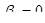 . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики 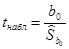 , которая при истинности гипотезы
, которая при истинности гипотезы  ,
,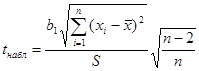 .
. .
.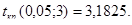 Так как наблюдаемое значение t-статистики больше критического значения, то гипотеза о равенстве коэффициента регрессии
Так как наблюдаемое значение t-статистики больше критического значения, то гипотеза о равенстве коэффициента регрессии  сводится к проверке гипотезы
сводится к проверке гипотезы 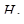 :
: 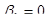 . Проверка осуществляется на основе статистики
. Проверка осуществляется на основе статистики  , которая при истинности гипотезы
, которая при истинности гипотезы  , откуда
, откуда 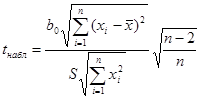 .
. .
. и числа степеней свободы v=5-2=3:
и числа степеней свободы v=5-2=3:  . Так как наблюдаемое значение t-статистики по модулю больше критического значения, то гипотеза о равенстве коэффициента регрессии
. Так как наблюдаемое значение t-статистики по модулю больше критического значения, то гипотеза о равенстве коэффициента регрессии 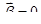 отвергается, то представляет интерес определение с надежностью
отвергается, то представляет интерес определение с надежностью  интервальных оценок параметров регрессии. При построении доверительных интервалов исходят из распределения соответствующих статистик. Интервальные оценки имеют вид:
интервальных оценок параметров регрессии. При построении доверительных интервалов исходят из распределения соответствующих статистик. Интервальные оценки имеют вид: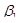 :
: ; (2.102)
; (2.102)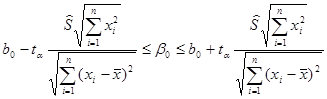 ; (2.103)
; (2.103)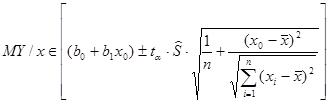 ; (2.104)
; (2.104) . (2.105)
. (2.105) – выборочная оценка несмещенного остаточного среднего квадратического отклонения;
– выборочная оценка несмещенного остаточного среднего квадратического отклонения; определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы v=n-2. При больших объемах выборки (по крайней мере, n>30) можно пользоваться табл. 1 Приложений нормального закона распределения.
и числа степеней свободы v=n-2. При больших объемах выборки (по крайней мере, n>30) можно пользоваться табл. 1 Приложений нормального закона распределения. с надежностью
с надежностью 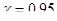 ;
;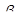 с надежностью
с надежностью 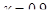 ;
;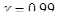 построить интервальную оценку условного математического ожидания My|x при х0=6;
построить интервальную оценку условного математического ожидания My|x при х0=6;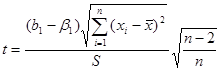 имеет t-распределение с числом степеней свободы v=n-2. Из этого следует, что генеральный коэффициент регрессии
имеет t-распределение с числом степеней свободы v=n-2. Из этого следует, что генеральный коэффициент регрессии  с надежностью
с надежностью  будет находиться внутри интервала, определяемого формулой:
будет находиться внутри интервала, определяемого формулой: ,
, и числа степеней свободы v=n-2. Длина доверительного интервала составит:
и числа степеней свободы v=n-2. Длина доверительного интервала составит: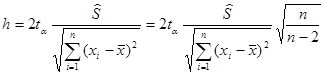 .
.
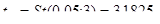 Воспользовавшись данными вспомогательной таблицы, получим:
Воспользовавшись данными вспомогательной таблицы, получим: 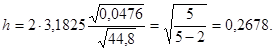
 определим по формуле
определим по формуле ,
, и числа степеней свободы v=n-2.
и числа степеней свободы v=n-2.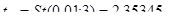 На основе расчетов, представленных во вспомогательной таблице, получим:
На основе расчетов, представленных во вспомогательной таблице, получим: .
.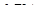 равна
равна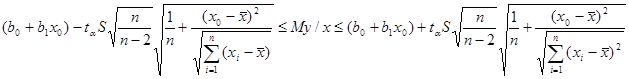 где
где 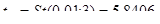 Воспользовавшись данными вспомогательной таблицы при х0=6, получим:
Воспользовавшись данными вспомогательной таблицы при х0=6, получим: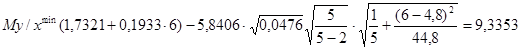 ;
; .
.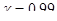 условное математическое ожидание My|х=6 будет лежать в пределах:
условное математическое ожидание My|х=6 будет лежать в пределах: 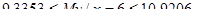
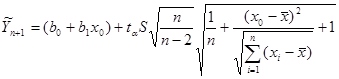 ,
,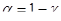 и числа степеней свободы v=n-2.
и числа степеней свободы v=n-2.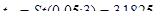 На основе расчетов, представленных во вспомогательной таблице, при х0=10, получим:
На основе расчетов, представленных во вспомогательной таблице, при х0=10, получим:




