Эта модель основана на марковском процессе, протекающем в дискретной системе с непрерывным временем.
Процесс, протекающий в системе, называется марковским (или процессом без последствий), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящее время 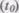 и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПО рассматривается как марковский процесс.
и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПО рассматривается как марковский процесс.
В начальный момент тестирования  в ПО было
в ПО было  ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы
ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы 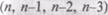 и т.д. соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая еще не обнаружена. Например, в состоянии
и т.д. соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая еще не обнаружена. Например, в состоянии  пятая ошибка уже исправлена, а шестая еще не обнаружена.
пятая ошибка уже исправлена, а шестая еще не обнаружена.
Последовательность состояний 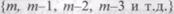 соответствует периодам времени, когда ошибки исправляются. Например, в состоянии
соответствует периодам времени, когда ошибки исправляются. Например, в состоянии  вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью X, а исправляются с интенсивностью
вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью X, а исправляются с интенсивностью  .
.
Статические модели надежности
Статические модели принципиально отличаются от динамических прежде всего тем, что в них не учитывается время появления ошибок в процессе тестирования и не используется никаких предположений о поведении функции риска 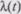 . Эти модели строятся на твердом статистическом фундаменте.
. Эти модели строятся на твердом статистическом фундаменте.
Модель Миллса
Использование этой модели предполагает необходимость перед началом тестирования искусственно вносить в программу ("засорять") некоторое количество известных ошибок. Ошибки вносятся случайным образом и фиксируются в протоколе искусственных ошибок. Специалист, проводящий тестирование, не знает ни количества, ни характера внесенных ошибок до момента оценки показателей надежности по модели Миллса. Предполагается, что все ошибки (как естественные, так и искусственно внесенные) имеют равную вероятность быть найденными в процессе тестирования.
Тестируя программу в течение некоторого времени, собирают статистику об ошибках. В момент оценки надежности но протоколу искусственных ошибок все ошибки делятся на собственные и искусственные. Соотношение

дает возможность оценить N − первоначальное число ошибок в программе. В данном соотношении, которое называется формулой Миллса, S − количество искусственно внесенных ошибок, п − число найденных собственных ошибок, V − число обнаруженных к моменту оценки искусственных ошибок.
Вторая часть модели связана с проверкой гипотезы от N. Предположим, что в программе имеется К собственных ошибок, и внесем в нее еще S ошибок. В процессе тестирования были обнаружены все S внесенных ошибок и п собственных ошибок.
Тогда по формуле Миллса мы предполагаем, что первоначально в программе было N = п ошибок. Вероятность, с которой можно высказать такое предположение, возможно рассчитать по следующему соотношению:

Таким образом, величина С является мерой доверия к модели и показывает вероятность того, насколько правильно найдено значение N. Эти два связанных между собой по смыслу соотношения образуют полезную модель ошибок: первое предсказывает возможное число первоначально имевшихся в программе ошибок, а второе используется для установления доверительного уровня прогноза.
Модель Липова
Липов модифицировал модель Миллса, рассмотрев вероятность обнаружения ошибки при использовании различного числа тестов. Если сделать то же предположение, что и в модели Миллса, т.е. что собственные и искусственные ошибки имеют равную вероятность быть найденными, то вероятность обнаружения п собственных и V внесенных ошибок равна:
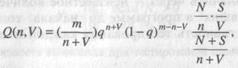
где т − количество тестов, используемых при тестировании;
q − вероятность обнаружения ошибки в каждом из т тестов, рассчитанная по формуле
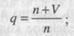
S − общее количество искусственно внесенных ошибок; N − количество собственных ошибок, имеющихся в ПО до начала тестирования.
Для использования модели Липова должны выполняться следующие условия:
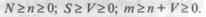
Оценки максимального правдоподобия (наиболее вероятное значение для N)задаются соотношениями

Модель Липова дополняет модель Миллса, давая возможность оценить вероятность обнаружения определенного количества ошибок к моменту оценки.
Простая интуитивная модель
Использование этой модели предполагает проведение тестирования двумя группами программистов (или двумя программистами в зависимости от величины программы) независимо друг от друга, использующими независимые тестовые наборы. В процессе тестирования каждая из групп фиксирует все найденные ею ошибки. При оценке числа оставшихся в программе ошибок результаты тестирования обеих групп собираются и сравниваются.
Получается, что первая группа обнаружила  ошибок, вторая −
ошибок, вторая − 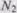 , а
, а  − это ошибки, обнаруженные обеими группами.
− это ошибки, обнаруженные обеими группами.
Если обозначить через N неизвестное количество ошибок, присутствовавших в программе до начала тестирования, то можно эффективность тестирования каждой из групп определить как
Предполагая, что возможность обнаружения всех ошибок одинакова для обеих групп, можно допустить, что если первая группа обнаружила определенное количество всех ошибок, она могла бы определить то же количество любого случайным образом выбранного подмножества. В частности, можно допустить:
Из формулы (18) 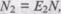 подставив в (19), получим:
подставив в (19), получим:
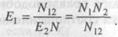
Модель Коркорэна
Модель Коркорэна относится к статическим моделям надежности ПО, так как в ней не используются параметры времени тестирования и учитывается только результат N испытаний, в которых выявлено 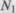 ошибок
ошибок  -го типа. Модель использует изменяющиеся вероятности отказов для различных типов ошибок.
-го типа. Модель использует изменяющиеся вероятности отказов для различных типов ошибок.
В отличие от двух рассмотренных выше статических моделей, по модели Коркорэна оценивается вероятность безотказного выполнения программы на момент оценки:
где  − число безотказных выполнений программы;
− число безотказных выполнений программы;
 − общее число прогонов;
− общее число прогонов;
К − априори известное число типов.


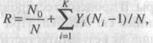

 − вероятность выявления при тестировании ошибки
− вероятность выявления при тестировании ошибки  -го типа.
-го типа.
В этой модели вероятность  должна оцениваться на основе априорной информации или данных предшествующего периода функционирования однотипных программных средств.
должна оцениваться на основе априорной информации или данных предшествующего периода функционирования однотипных программных средств.
Модель Нельсона
Данная модель при расчете надежности ПО учитывает вероятность выбора определенного тестового набора для очередного выполнения программы.
Предполагается, что область данных, необходимых для выполнения тестирования программного обеспечения, разделяется на К взаимоисключающих подобластей 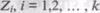 . Пусть
. Пусть 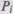 − вероятность того, что набор данных
− вероятность того, что набор данных 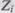 будет выбран для очередного выполнения программы. Предполагая, что к моменту оценки надежности было выполнено
будет выбран для очередного выполнения программы. Предполагая, что к моменту оценки надежности было выполнено 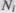 прогонов программы на
прогонов программы на 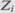 наборе данных и из них
наборе данных и из них  количество прогонов закончилось отказом, надежность ПО в этом случае равна:
количество прогонов закончилось отказом, надежность ПО в этом случае равна:

На практике вероятность выбора очередного набора данных для прогона 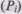 определяется путем разбиения всего множества значений входных данных на подмножества и нахождения вероятностей того, что выбранный для очередного прогона набор данных будет принадлежать конкретному подмножеству. Определение этих вероятностей основано на эмпирической оценке вероятности появления тех или иных входов в реальных условиях функционирования.
определяется путем разбиения всего множества значений входных данных на подмножества и нахождения вероятностей того, что выбранный для очередного прогона набор данных будет принадлежать конкретному подмножеству. Определение этих вероятностей основано на эмпирической оценке вероятности появления тех или иных входов в реальных условиях функционирования.



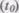 и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПО рассматривается как марковский процесс.
и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПО рассматривается как марковский процесс. в ПО было
в ПО было  ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы
ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы 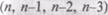 и т.д. соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая еще не обнаружена. Например, в состоянии
и т.д. соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая еще не обнаружена. Например, в состоянии  пятая ошибка уже исправлена, а шестая еще не обнаружена.
пятая ошибка уже исправлена, а шестая еще не обнаружена.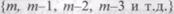 соответствует периодам времени, когда ошибки исправляются. Например, в состоянии
соответствует периодам времени, когда ошибки исправляются. Например, в состоянии  вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью X, а исправляются с интенсивностью
вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью X, а исправляются с интенсивностью  .
.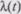 . Эти модели строятся на твердом статистическом фундаменте.
. Эти модели строятся на твердом статистическом фундаменте.

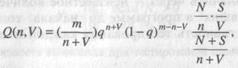
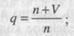
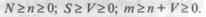

 ошибок, вторая −
ошибок, вторая − 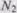 , а
, а  − это ошибки, обнаруженные обеими группами.
− это ошибки, обнаруженные обеими группами.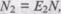 подставив в (19), получим:
подставив в (19), получим: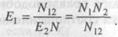
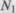 ошибок
ошибок  -го типа. Модель использует изменяющиеся вероятности отказов для различных типов ошибок.
-го типа. Модель использует изменяющиеся вероятности отказов для различных типов ошибок. − число безотказных выполнений программы;
− число безотказных выполнений программы; − общее число прогонов;
− общее число прогонов;

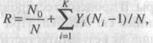

 − вероятность выявления при тестировании ошибки
− вероятность выявления при тестировании ошибки  -го типа.
-го типа. должна оцениваться на основе априорной информации или данных предшествующего периода функционирования однотипных программных средств.
должна оцениваться на основе априорной информации или данных предшествующего периода функционирования однотипных программных средств.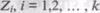 . Пусть
. Пусть 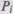 − вероятность того, что набор данных
− вероятность того, что набор данных 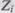 будет выбран для очередного выполнения программы. Предполагая, что к моменту оценки надежности было выполнено
будет выбран для очередного выполнения программы. Предполагая, что к моменту оценки надежности было выполнено 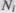 прогонов программы на
прогонов программы на 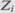 наборе данных и из них
наборе данных и из них  количество прогонов закончилось отказом, надежность ПО в этом случае равна:
количество прогонов закончилось отказом, надежность ПО в этом случае равна:
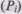 определяется путем разбиения всего множества значений входных данных на подмножества и нахождения вероятностей того, что выбранный для очередного прогона набор данных будет принадлежать конкретному подмножеству. Определение этих вероятностей основано на эмпирической оценке вероятности появления тех или иных входов в реальных условиях функционирования.
определяется путем разбиения всего множества значений входных данных на подмножества и нахождения вероятностей того, что выбранный для очередного прогона набор данных будет принадлежать конкретному подмножеству. Определение этих вероятностей основано на эмпирической оценке вероятности появления тех или иных входов в реальных условиях функционирования.


