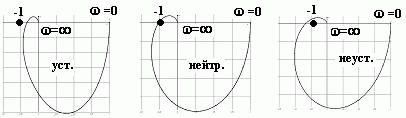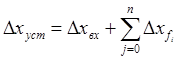РЕФЕРАТ
На тему: применение методов спектрального анализа при решение задач теории автоматического регулирования, частотные методы исследования устойчивости линейных автоматических систем
Выполнил Смирнов Иван Сергеевич гр 3-35
специальность __АТПП____________________
15.03.04
Предмет: «Кибернетика»,
Руководитель: __Невиницин Владимер Юрьевич ______________
Ф.И.О. (полностью), преподаватель ____ (высшей, первой, второй) квалификационной категории
Работа допущена к защите «__»____2019г.
Оценка: ___________________________
Иваново, 2019
СПЕКТРАЛЬНЫЙ АНАЛИЗ
И ЕГО ПРИЛОЖЕНИЯ К ЗАДАЧАМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Г л а в а 1
РЯДЫ И ИНТЕГРАЛ ФУРЬЕ
§ 12.1. Ряды Фурье
А. Гармонический анализ
В теории и практике автоматического управления часто встречаются процессы, которые можно рассматривать как периодические.
Функция называется периодической, если при некотором постоянном числе T > 0 выполняется равенство
| f (t)= f (t + nT),
| (12.1)
|
где T — период функции; n — любое целое число (положи-тельное или отрицательное); t — аргумент, принимает зна-чения из области определения этой функции.
Периодическая функция f (t) с периодом Т характеризу-
ется тем, что интеграл от этой функции, взятый в интервале длиной Т, не меняется при изменении пределов интегриро-вания при условии, что длина интервала интегрирования ос-тается равной T, т. е.
| a + T
| b + T
|
|
|
| ∫
| f (t) dt =∫ f (t) dt
| (12.2)
|
|
| a
| b
|
|
|
| при любых a и b.
|
| 0 < b < T,
|
|
| Действительно, пусть, например, 0 < a < T,
|
|
| тогда
|
|
|
|
3
Часто функцию F (j ω) называют, используя терминологию
спектрального анализа периодических функций, условно ком-плексным амплитудным частотным спектром непериоди-ческой функции f (t), а функцию | F (j ω)| — амплитудным час-
тотным спектром этой функции.Такая терминология можетпривести к неудобству, если приходится сравнивать спектраль-ные представления для периодических и непериодических функций. Следует еще раз подчеркнуть, что амплитудный час-тотный спектр A k периодической функции характеризует рас-
пределение амплитуд гармоник разложения по частотам этих гармоник, а модуль | F (j ω)| спектральной плотности неперио-
дической функции — распределение относительных амплитуд гармоник разложения. Однако термин «спектральная плот-ность» также не является удачным, поскольку его использо-вание тоже может привести к недоразумениям, так как подобная терминология используется в теории случайных процессов для обозначения распределения мощности флюк-туации стационарного случайного процесса по спектру частот.
В § 22.3 (т. 3) указанное распределение мощности называется спектральной плотностью мощности (или просто спектраль-
ной плотностью). Поскольку применительно к случайным процессам название спектральная плотность является обще-употребительным, то мы в дальнейшем будем избегать назы-вать функцию F (j ω) спектральной плотностью, оставляя за ней название спектральная характеристика.
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Свойства преобразования Фурье a. Прямое и обратное преобразования
Выше, в § 12.2, отмечалось, что преобразованию Фурье мо-гут быть подвергнуты функции f (t), удовлетворяющие усло-виям Дирихле и являющиеся абсолютно интегрируемыми на всей оси 0 t.
62
Найдем связь между спектральными характеристиками F t (j ω)и F T (j ω, t).Формулу(13.81)перепишем в сле-дующем виде:
| t
| t − T
|
| F T (j ω, t)=∫ f (t) e − j ω t dt −∫ f (t) e − j ω t dt.
|
| 0
| 0
|
Правая часть этого равенства представляет собой раз-ность двух текущих спектральных характеристик для функ-
| ции f (t). Обозначим эту разность
| через F t (j ω), тогда
|
|
| F (j ω, t)=
| F (j ω),или
| F T (j ω, t)
| =
|
| F t (j ω)
| .
|
|
|
|
|
|
|
| T
| t
| T
|
|
| T
|
|
|
|
|
|
|
|
Если значение Т выбрано достаточно малым, то будет справедлива приближенная формула
| F T (j ω, t)≈ T
| ∂ F t (j ω)
| .
| (13.82)
|
|
| ∂ t
|
|
|
|
|
|
|
Г л а в а 2
ПРИМЕНЕНИЕ МЕТОДОВ СПЕКТРАЛЬНОГО
АНАЛИЗА ПРИ РЕШЕНИИ ЗАДАЧ
ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
§ 14.1. Спектры сигналов в системах автоматического управления. Частотные характеристики
а. Преобразование линейной системой гармонического
Входного сигнала.
Определение установившегося процесса
Рассмотрим линейную автоматическую систему, описы-ваемую дифференциальным уравнением n -го порядка с по-стоянными коэффициентами
| (a
| p n + a p n −1
| +... + a
| n −1
| p + a) x (t)=
|
|
|
| 0
| 1
|
| n
| (14.1)
|
|
| = (b 0 p m + b 1 p m −1... + b m −1 p + b m) g (t),
|
|
|
|
|
107
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
И ЕГО ПРИМЕНЕНИЕ ПРИ АНАЛИЗЕ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Г л а в а 3
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
§ 15.1. Преобразование Лапласа
А. Основные понятия
Операционное исчисление нашло широкое применение в теории автоматического управления, где с его помощью про-изводится анализ переходных и установившихся процессов в автоматических системах. Сущность метода операционного исчисления заключается в следующем. Пусть задана некото-рая функция f (t) действительной переменной t, причем такая, что для нее существует преобразование Лапласа (L-преоб-разование)
∞
L[ f (t)] = F (s) = ∫ f (t) e − st dt,
0
т. е. интеграл в правой части этого равенства является схо-дящимся. Используя L-преобразование, можно каждой пре-образуемой по Лапласу функции f (t) (такие функции со-
ставляют класс функций, называемых оригиналами) поста-вить в соответствие функцию F (s) комплексной переменной s (при этом функция F (t) называется изображением функции f (s)).Преобразование Лапласа имеет ряд замечательныхсвойств. Например, дифференцированию оригинала f (t) по
переменной t соответствует операция умножения на
комплексную переменную s, а интегрированию оригинала
164
Рис. 16.1
Г л а в а 4
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА ДЛЯ ИССЛЕДОВАНИЯ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
§ 16.1. Передаточные функции и частотные характеристики системы
Рассмотрим некоторые вопросы, связанные с применени-ем преобразования Лапласа при исследовании непрерывных систем автоматического управления. Будем полагать, что процессы, происходящие в системе, описываются линейны-ми дифференциальными уравнениями
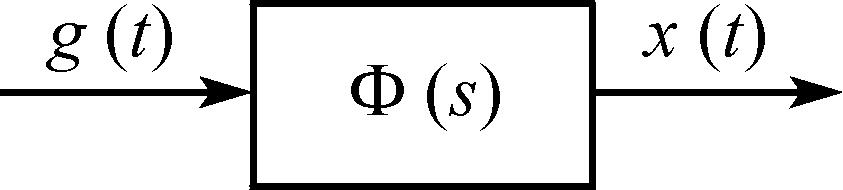
с постоянными коэффициентами. Та-ким образом, мы ограничимся в на-
стоящей главе рассмотрением линей-ных систем с постоянными парамет-
рами, т. е. не зависящими ни от времени, ни от состояния системы.
Пусть дифференциальное уравнение автоматической системы (рис. 16.1) записано в операторной форме (см. § 6.1, т. 1):
| D (p) x (t)= M (p) g (t),
| (16.1)
|
где D (p) и M (p) — многочлены от p:
| D (p)= a p n + a p −1
| +... + a
| n −1
| p + a;
|
|
|
| 0
| 1
|
|
| n
| (16.2)
|
|
| M (p)= b p m + b p m −1+...+ b
|
| p + b
|
|
|
| ,
|
|
| 0
| 1
|
| m −1
| m
|
|
p — оператор дифференцирования; x (t) — выходная коорди-ната системы; g (t) — управляющее воздействие.
Преобразуем уравнение (16.1) по Лапласу, предположив нулевые начальные условия. Введя обозначения X (s) =
= L[ x (t)], G (s) = L [ g (t)], получим
| D (s) X (s) = M (s) G (s),
| (16.3)
|
РАЗНОСТНЫЕ УРАВНЕНИЯ.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. МЕТОДЫ ИССЛЕДОВАНИЯ ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Г л а в а 5
Рис. 17.1
функции, определенные только в равноотстоящих точках t =
= nT,где n —любое целое число,а T — постоянная,называе-мая периодом дискретности. Эти функции принято обозна-
чать f [ nT ] (рис. 17.1).
255
В последнем равенстве w [ n ] — решение однородного
уравнения (17.114) и, следовательно, все слагаемые, стоящие под знаком суммы, обращаются в ноль. Таким образом, уравнение (17.130) обращается в тождество, т. е. дискретная функция x [ n ], определенная по формуле (17.127), является его решением.
Рассмотренный прием позволяет определять общий вид решения неоднородного разностного уравнения общего вида (17.130), часто встречающегося в теории дискретных систем автоматического управления.
Задача решения разностных уравнений с постоянными коэффициентами существенно упрощается при использова-нии дискретного преобразования Лапласа, которое рассмот-рено в гл. 19.
Глава 6
Автоматического управления
Понятие дискретной системы связано с понятием дискрет-ного сигнала, т. е. сигнала, значения которого определены только в дискретные моменты времени t i (i = 1, 2, …, n, …). Возникновение дискретных сигналов в автоматических сис-темах может быть обусловлено различными причинами. Пер-вая причина — это специальная дискретизация сигнала, кото-рая выполняется, например, в целях защиты сигнала от помех при его передаче по каналу связи, или в целях передачи не-скольких сигналов по одному и тому же каналу. В этом случае непрерывный сигнал заменяется последовательностью им-пульсов, один из параметров которых (амплитуда, ширина, частота) содержит информацию о дискретных значениях сиг-
336
Разностное уравнение (18.53) для вектора состояния не-прерывной части теперь примет вид
x 2[(n + 1) T ] = e A 2 T x 2[ nT ] +
| + e A 2 T B ∗ K (C x
| [ nT ] + D ε[ nT ]),
| (18.61)
|
| 2
| и 1 1
| 1
|
|
| | | | |
а вектор выходного сигнала цифровой системы в дискретные моменты времени y [ nT ] определится из равенства:
y [ nT ] = C 2 x 2[ nT ] + D 2 K и(C 1 x 1[ nT ] + D 1 ε [ nT ]). (18.62)
Этот вектор можно определить и в произвольные момен-ты времени с учетом уравнения (18.57), которое для замкну-той цифровой системы можно записать в виде:
y T [ n,ε] = C 2 x 2 T [ n,ε] + D 2 K и(C 1 x 1 T [ n ] + D 1 ε T [ n ]),
где x 2 T [ n, ε ] — вектор состояния непрерывной части систе-мы в произвольные моменты времени, определяемый равен-ством (18.58):
x 2 T [ n,ε] = e A 2ε T x 2 T [ n ] + Т В *(ε) K и(C 1 x 1 T [ n ] + D 1 ε T [ n ]).
Таким образом, линейные разностные уравнения позво-ляют построить математические модели, описывающие ши-рокий класс дискретных автоматических систем, содержа-щих как непрерывные, так и цифровые устройства.
Устойчивость САУ
Понятие устойчивости является важнейшей качественной оценкой динамических свойств САУ. Устойчивость САУ связана с характером её поведения после прекращения внешнего воздействия, которое может быть оценено решением дифференциального уравнения, описывающего работу системы. Общая теория устойчивости разработана А.М. Ляпуновым. Линейная система называется устойчивой, если ее выходная координата остается ограниченной при любых ограниченных по абсолютной величине входных воздействиях. Устойчивость линейной системы определяется ее характеристиками и не зависит от действующих воздействий.
В общем случае решение уравнения имеет вид: y(t)= yB (t) + yn (t)
где yB (t) – решение однородного уравнения (переходная или свободная составляющая); yn (t) – установившееся значение регулируемой величины (вынужденная составляющая) – решение уравнения с правой частью. Устойчивость работы системы определяется переходной составляющей. Если переходная составляющая процесса управления после прекращения внешнего воздействия стремится к нулю, то такая система является устойчивой. Другими словами устойчивость системы – это есть затухание ее переходных процессов.
Если свободная составляющая стремится к конечному значению или имеет вид гармонических колебаний с постоянной амплитудой, то система считается нейтральной. В том случае, если свободная составляющая неограниченно возрастает или имеет вид гармонических колебаний с возрастающей амплитудой, то система считается неустойчивой. Оценка устойчивости производится на основе результатов исследования свободной составляющей, которая представляет собой решение однородного дифференциального уравнения (характеристического уравнения):
D(p) = a0 pn + a1 pn-1 +… + an = 0
Переходная составляющая решения уравнения в общем виде yni (t) = Ai eα i t * sin(βi t + φi), где αi ± jβi – корни характеристического уравнения; Ai,Φi – постоянные.
При этом переходная составляющая с ростом времени стремится к нулю, если вещественные части корней αi отрицательны, в противном случае амплитуда колебаний переходной составляющей возрастает.
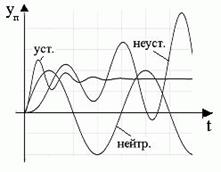
Рис. 2. Графики переходных составляющих
Пара мнимых корней (αi =0) характеристического уравнения позволяет получить переходную составляющую в виде автоколебаний с постоянной амплитудой:
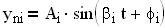
Полученные корни характеристического уравнения могут быть представлены в виде точек на комплексной плоскости.
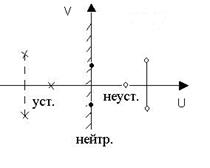
Рис. 3. Расположение корней САУ на комплексной плоскости
Для устойчивых систем необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости корней. Если хотя бы один вещественный корень или пара комплексных сопряженных корней находится справа от мнимый оси, то система является неустойчивой. Если имеется нулевой корень или пара чисто мнимых корней, то система считается нейтральной (находящейся на границе устойчивости и неустойчивости). Таким образом, мнимая ось комплексной плоскости является границей устойчивости.
С целью упрощения анализа устойчивости систем разработаны ряд специальных методов, которые получили название критерии устойчивости. Критерии устойчивости делятся на две разновидности: алгебраические (критерий Гурвица) и частотные (критерии Михайлова и Найквиста).
Алгебраический критерий устойчивости Гурвица находит широкое применение при анализе САУ. Первоначально, из коэффициентов уравнения составляется матрица главного определителя:

По диагонали матрицы от верхнего левого угла записываются по порядку все коэффициенты уравнения, начиная с 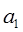 . Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз – уменьшались.
. Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз – уменьшались.
Для устойчивости системы необходимо и достаточно, чтобы при  все угловые определители (миноры) были также положительными.
все угловые определители (миноры) были также положительными.
Последний определитель Гурвица, как видно из приведенной выше матрицы, равен Δn =an *Δn-1. Поэтому его положительность сводится при Δn-1 >0 к условию an >0. Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов 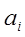 . Если определитель Δn =0, то система находится на границе устойчивости. Из условия Δn-1 =0 можно определить параметры, при которых система находится на границе устойчивости, например, критический коэффициент усиления разомкнутой САУ.
. Если определитель Δn =0, то система находится на границе устойчивости. Из условия Δn-1 =0 можно определить параметры, при которых система находится на границе устойчивости, например, критический коэффициент усиления разомкнутой САУ.
Частотный критерий устойчивости Михайлова предполагает построение годографа на комплексной плоскости. Для построения годографа из характеристического уравнения замкнутой системы путем подстановки p=jω получают аналитическое выражение вектора M(jω):
M(jω)=a0 (jω)n +a1 (jω)n-1 + … +an
Уравнение является комплексным и может быть представлено в виде:

Построение годографа производится по уравнению вектора M(jω) при изменении частоты от 0 до 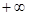 . Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω<
. Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω< 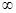 .
.
Тогда для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента годографа M(jω) при изменении от 0 до + 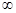 равнялось n.
равнялось n.
Критерий Михайлова формулируется так: система устойчива, если годограф Михайлова M(jω) при изменении от 0 до 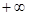 , начинаясь на положительной части действительной оси, обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов и в n-м квадранте уходил в
, начинаясь на положительной части действительной оси, обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов и в n-м квадранте уходил в 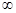 .
.
Если годограф начинается в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной. В этом случае U(ω) = 0 и V(ω) = 0.
Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости (критические значения). На рис. 4 приведены годографы Михайлова для устойчивых и неустойчивых САУ.
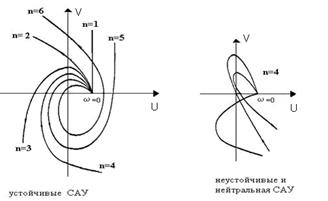
Рис. 4. Годографы Михайлова
Имеется вторая формулировка критерия Михайлова: для устойчивости системы необходимо и достаточно, чтобы корни уравнений U(ω) = 0 и V(ω) = 0 перемежались (чередовались), т.е. годограф последовательно пересекал оси комплексной плоскости. Этой формулировкой удобно пользоваться для исследования устойчивости систем до пятого порядка включительно. По уравнению можно определить количество правых корней в неустойчивых системах.
Частотный критерий устойчивости Найквиста, позволяющий по виду амплитудно-фазовой частотной характеристики разомкнутой системы оценить устойчивость работы замкнутой системы. АФЧХ может быть получена экспериментально или аналитически. Аналитическое построение АФЧХ производится обычными методами. Критерий Найквиста формулируется так:
если разомкнутая система устойчивая, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до 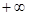 не охватывала точку с координатами -1, j0. Если АФЧХ разомкнутой системы проходит через точку с координатами -1, j0, то система будет нейтральной. На рис. 5 представлены АФЧХ разомкнутых статических систем. Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы.
не охватывала точку с координатами -1, j0. Если АФЧХ разомкнутой системы проходит через точку с координатами -1, j0, то система будет нейтральной. На рис. 5 представлены АФЧХ разомкнутых статических систем. Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы.
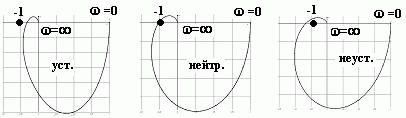
Рис. 5.АФЧХ разомкнутых САУ
Существуют два класса САУ: абсолютно устойчивые и условно устойчивые. В первом классе систем только увеличение коэффициента усиления разомкнутой системы может привести к потере устойчивости, а условно устойчивая система может стать неустойчивой как при увеличении, так и при уменьшении коэффициента усиления.
Для абсолютно устойчивых систем вводится понятие запаса устойчивости по амплитуде (модулю) и запаса устойчивости по фазе. Запасы устойчивости определяют на частоте среза ωср, на которой A(ωср)=1.
Запас устойчивости по амплитуде задается некоторой величиной, которая показывает, во сколько раз можно увеличить коэффициент усиления разомкнутой системы, чтобы САУ оказалась на границе устойчивости.
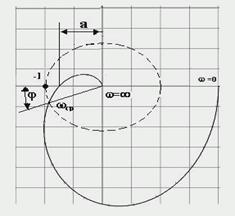
Рис. 6.АФЧХ абсолютно устойчивой системы
Точность линейных САУ
Устойчивость САУ является важной, но не полной характеристикой работы системы. Кроме устойчивости система должна обладать требуемой точностью и требуемым качеством переходных процессов. Установившийся режим может быть статичен и динамичен. Статический режим – это режим, при котором входное воздействие после появления остается неизменным. Динамический установившийся режим – это режим, при котором входное воздействие изменяется по какому-то закону.
С точки зрения точности работы системы они могут быть статическими и астатическими.
Астатические системы могут быть I, II, III и т.д. порядка (определяется количеством интегрирующих звеньев). Что касается установившейся ошибки Δхуст, то в соответствии с принципом суперпозиции равна:
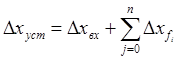
где Δхвх – ошибка входного воздействия,
Δхfj – ошибка от возмущающего воздействия,
n – количество возмущающих воздействий.
Составленные ошибки могут определяться по теории о конечном значении функции, по реакции на типовые воздействия и по коэффициенту ошибок.
С П И С О К Л И Т Е Р А Т У Р Ы
1. Демидович Б.П., Моденов В.П. Дифференциальные уравне-ния. М.: Изд-во «Лань», 2006.
2. Ким Д.П. Теория автоматического управления.В3т.Т. 1.
М.: Физматгиз, 2003.
3. Пискунов Н.С. Дифференциальное и интегральное исчисле-ния. М.: Интегра-Пресс, 2001.
4. Толстов Г.П. Ряды Фурье.М.:Наука, 1980.
5. Фихтенгольц Г.М. Курс дифференциального и интегрально-го исчисления. В 3 т. Т. 3. М.: Физматгиз, 2005.
6. Харкевич А.А. Спектры и анализ.М.:Физматгиз, 1962.
Список источников
https://www.bestreferat.ru/referat-254793.html
http://baumanpress.ru/books/108/108.pdf
О Г Л А В Л Е Н И Е
И ЕГО ПРИЛОЖЕНИЯ К ЗАДАЧАМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ........................ 3
Глава 12. РЯДЫ И ИНТЕГРАЛ ФУРЬЕ.............................................. 3
§ 12.1. Ряды Фурье............................................................................................... 3
а. Гармонический анализ........................................................................ 3
б. Сходимость ряда Фурье.................................................................. 19
в. Разложение в интервале (0, π)..................................................... 30
г. Функции с периодом T...................................................................... 33
д. Комплексная форма ряда Фурье................................................ 37
е. Понятие о спектрах............................................................................ 40
§ 12.2. Интеграл Фурье................................................................................... 45
а. Предельный переход от ряда Фурье
к интегралу Фурье............................................................................... 45
б. Комплексная форма интеграла Фурье.................................... 52
Глава 13. ПРЕОБРАЗОВАНИЕ ФУРЬЕ............................................ 62
§ 13.1. Свойства преобразования Фурье............................................... 62
а. Прямое и обратное преобразования......................................... 62
б. Спектральные характеристики суммы,
производной и интеграла................................................................ 68
в. Спектральная характеристика смещенной функции.
Смещение спектральной характеристики.
Сжатие и растяжение функции..................................................... 72
г. Теорема Парсеваля............................................................................. 77
д. Умножение спектральных характеристик.
Спектральная характеристика произведения
двух функций 81
§ 13.2. Спектральные характеристики некоторых функций...... 87
а. Единичная ступенчатая функция. Дельта-функция......... 87
б. Гармонические колебания............................................................. 97
§ 13.3. Спектральные характеристики, зависящие
от времени 101
Глава 14. ПРИМЕНЕНИЕ МЕТОДОВ СПЕКТРАЛЬНОГО
СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ............................................................................ 235
§ 16.1. Передаточные функции и частотные характеристики
системы................................................................................................... 235
611
§ 16.2. Определение процессов в системах автоматического
управления............................................................................................ 246
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА.
МЕТОДЫ ИССЛЕДОВАНИЯ
ДИСКРЕТНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ..................... 255
Глава 17. ЭЛЕМЕНТЫ ТЕОРИИ РАЗНОСТНЫХ
УРАВНЕНИЙ.............................................................................. 255
§ 17.1. Дискретные функции и действия над ними....................... 255
а. Определение дискретной функции......................................... 255
б. Конечные разности дискретных функций.......................... 257
в. Суммирование дискретных функций..................................... 263
§ 17.2. Разностные уравнения. Основные понятия
и определения...................................................................................... 269
а. Разностное уравнение и его решение.................................... 269
б. Системы разностных уравнений.............................................. 271
в. Нормальная система разностных уравнений.................... 273
§ 17.3. Линейные разностные уравнения............................................ 274
а. Системы линейных разностных уравнений.
Формула Коши................................................................................... 274
б. Однородные системы разностных уравнений.................. 276
в. Неоднородные системы линейных
разностных уравнений.................................................................... 281
г. Линейные разностные уравнения порядка k...................... 286
§ 17.4. Линейные разностные уравнения с постоянными
коэффициентами................................................................................ 302
а. Система однородных разностных уравнений
с постоянными коэффициентами. Случай простых
корней линейных характеристического уравнения....... 302
б. Случай кратных корней характеристического
уравнения............................................................................................... 304
в. Решение неоднородных систем разностных уравнений
с постоянными коэффициентами.............................................. 309
г. Решение линейных разностных уравнений порядка k
с постоянными коэффициентами.............................................. 317
Глава 18. РАЗНОСТНЫЕ УРАВНЕНИЯ
ДИСКРЕТНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ................... 336
§ 18.1. Разностные уравнения линейных
импульсных систем.......................................................................... 336
а. Общие сведения о дискретных системах
автоматического управления...................................................... 336
612
б. Разностные уравнения линейных импульсных систем 346
в. Разностные уравнения многомерных
импульсных систем......................................................................... 360
§ 18.2. Разностные уравнения цифровых систем........................... 363
а. Разностные уравнения управляющих
вычислительных устройств......................................................... 363
б. Разностные уравнения цифровых систем
автоматического управления..................................................... 374
Глава 19. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ
ЛАПЛАСА 378
§ 19.1. Дискретное преобразование Лапласа
и Z -преобразование.......................................................................... 378
а. Определение дискретного преобразования Лапласа
и Z -преобразования.......................................................................... 378
б. Формула обращения....................................................................... 384
§ 19.2. Основные свойства дискретного преобразования
Лапласа и Z -преобразования....................................................... 387
а. Линейность Z -преобразования................................................... 388
б. Смещение в области оригиналов
и в области Z -изображений......................................................... 388
в. Изображения конечных разностей и конечных сумм
дискретных функций....................................................................... 393
г. Свертка оригиналов и изображений....................................... 397
д. Дифференцирование и интегрирование изображений. 400
е. Теоремы о предельных значениях оригиналов
и изображений..................................................................................... 404
ж. Теорема о сумме квадратов значений
дискретной функции....................................................................... 406
§ 19.3. Связь между D -преобразованием и преобразованием
Лапласа. D - и Z -преобразования.............................................. 409
а. Определение D - и Z -преобразований..................................... 409
б. Свойства D -преобразования....................................................... 416
§ 19.4. Дискретное преобразование Фурье.
Дискретный ряд Фурье................................................................... 423
а. Определение и некоторые свойства дискретного
преобразования Фурье................................................................... 423
б. Связь между преобразованием Фурье непрерывных
и дискретных функций. Теорема Котельникова............. 430
в. Дискретный ряд Фурье.................................................................. 435
613
Глава 20. ПРИМЕНЕНИЕ ДИСКРЕТНОГО
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
ДЛЯ ИССЛЕДОВАНИЯ ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ. МЕТОД ПРОСТРАНСТВА СОСТОЯНИЙ............. 440
§ 20.1. Передаточные функции дискретных
автоматических систем.................................................................. 440
а. Способы определения передаточных функций
дискретных автоматических систем..................................... 440
б. Исследование процессов в дискретных автоматических
системах с использованием Z -преобразования................ 453
в. Решение разностных уравнений дискретной системы
с использованием Z -преобразования...................................... 457
§ 20.2. Частотные характеристики дискретных систем............. 466
а. Определение и свойства частотных характеристик
дискретных систем........................................................................... 466
б. Связь между частотными характеристиками
непрерывных и дискретных систем........................................ 470
в. w -преобразование и логарифмические частотные
характеристики дискретных систем....................................... 472
§ 20.3. Метод пространства состояний в теории дискретных
автоматических систем.................................................................. 477
а. Основные понятия............................................................................ 477
б. Определение уравнений состояния для линейных
дискретных систем с одним входом и одним выходом 479
в. Управляемость линейных дискретных автоматических
систем. Критерии управляемости............................................ 499
г. Наблюдаемость линейных дискретных автоматических
систем. Критерии наблюдаемости............................................ 503
д. Двойственность управляемости и наблюдаемости....... 511
е. Синтез модального управления для линейных
дискретных автоматических систем...................................... 512
ж. Уравнения наблюдающих устройств полного
и неполного порядка...................................................................... 518
Глава 21. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ.
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ТЕОРИИ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Том 2
Ющенко Аркадий Семенович
Редактор Н.Е. Овчеренко
Художник Н.Г. Столярова
Компьютерная графика Н.П. Новиковой
Технический редактор Э.А. Кулакова
Корректор Г.С. Беляева
Компьютерная верстка О.В. Беляевой
Оригинал-макет подготовлен
<



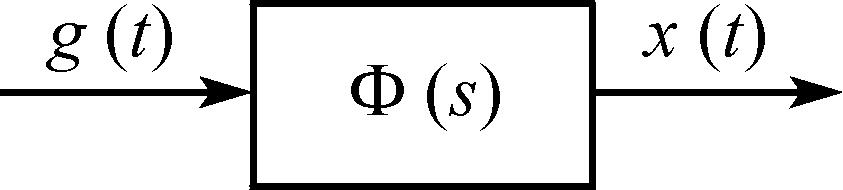

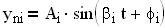


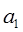 . Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз – уменьшались.
. Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз – уменьшались. все угловые определители (миноры) были также положительными.
все угловые определители (миноры) были также положительными.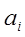 . Если определитель Δn =0, то система находится на границе устойчивости. Из условия Δn-1 =0 можно определить параметры, при которых система находится на границе устойчивости, например, критический коэффициент усиления разомкнутой САУ.
. Если определитель Δn =0, то система находится на границе устойчивости. Из условия Δn-1 =0 можно определить параметры, при которых система находится на границе устойчивости, например, критический коэффициент усиления разомкнутой САУ.
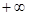 . Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω<
. Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω< 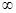 .
.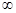 равнялось n.
равнялось n.