Симплекс-метод является универсальным, т.к. позволяет решить практически любую задачу линейного программирования.
Чаще всего, при графическом решении задач линейного программирования ОДР представляет собой замкнутый выпуклый многоугольник. В случае n переменных ОДР будет многомерным многогранником, подобным симплексу. Как правило, оптимальное решение – это координаты какой-либо вершины этого многогранника. Основная идея симплекс-метода заключается в последовательном целенаправленном обходе вершин такого симплекса. При этом в каждой следующей вершине симплекса значение целевой функции, в общем случае, улучшается.
Однако, перед применением симплекс – метода исходную задачу линейного программирования следует записать в канонической форме:

В канонической форме записи все переменные неотрицательны, а ограничениями являются уравнения. Переход от произвольной к канонической форме записи задачи линейного программирования производится с помощью следующих простых действий:
1. Если требуется найти минимум целевой функции L, то, заменяя функцию L на функцию (- L), переходят к задаче максимизации.
2. Если ограничение содержит неравенство со знаком «не более», то от него переходят к равенству, добавляя в левую часть ограничения дополнительную неотрицательную переменную.
3. Если ограничение содержит неравенство со знаком «не менее», то от него переходят к равенству, вычитая из левой части ограничения дополнительную неотрицательную переменную.
4. Если в задаче какая-либо из переменных произвольна по величине, то от нее избавляются, заменяя ее разностью двух других дополнительных неотрицательных переменных.
Задача линейного программирования, записанная в канонической форме, называется основной задачей линейного программирования.
Пусть записана основная задача линейного программирования. Предположим, что все уравнения системы ограничений независимы, т.е. выражают независимые друг от друга условия задачи. Если это не так, то лишние, зависимые от других, уравнения просто исключают. Основную задачу линейного программирования имеет смысл решать только тогда, когда число уравнений системы ограничений меньше числа входящих в них неизвестных, т.е. когда: m < n. В противном случае, если m = n, то система имеет единственное решение и пропадает смысл задачи максимизации, если же m > n, то система переопределена и, в общем случае, не имеет решения.
Итак, если количество линейно независимых уравнений строго меньше количества неизвестных (переменных), то система уравнений ограничений имеет бесконечное множество решений, и, следовательно, среди них можно выбирать оптимальное, т.е. то, которое доставляет максимум целевой функции задачи.
Реализация симплекс-метода включает в себя два крупных этапа:
1. Определение начального решения, удовлетворяющего ограничениям.
2. Последовательное улучшение начального решения и получение оптимального решения задачи.
Пусть система уравнений ограничений содержит ровно m линейно независимых уравнений, и, кроме того, m < n, тогда эту систему можно разрешить относительно m неизвестных, например:  , выразив их через остальные (n – m) неизвестные.
, выразив их через остальные (n – m) неизвестные.
После проведения таких преобразований основная задача линейного программирования оказывается записанной в стандартном виде:
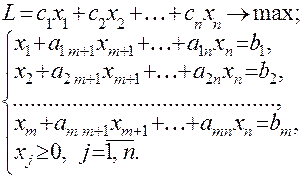
После того, как задача записана в стандартном виде, можно приступать к ее решению с помощью симплекс – метода, пошаговый алгоритм которого заключается в следующем:
Шаг 1. Получение начального решения. Выбираются m переменных, называемых базисными и обладающих следующим свойством: они входят с коэффициентом единица (безразлично, с плюсом или с минусом) только в одно уравнение системы ограничений, и с коэффициентом нуль (т.е. не входят) – в остальные уравнения системы ограничений.
Остальные (n – m) переменных называются свободными. При этом все свободные переменные полагают равными нулю, но тогда базисные переменные будут равны свободным членам уравнений системы ограничений.
Если m базисных переменных это:  (если это не так, то переменные всегда можно перенумеровать), тогда начальное решение будет иметь вид:
(если это не так, то переменные всегда можно перенумеровать), тогда начальное решение будет иметь вид:

Если все  , то начальное решение является допустимым, и можно переходить к шагу 2. В противном случае повторяют алгоритм поиска начального решения, т.е. преобразованиями уравнений системы ограничений добиваются выполнения условия
, то начальное решение является допустимым, и можно переходить к шагу 2. В противном случае повторяют алгоритм поиска начального решения, т.е. преобразованиями уравнений системы ограничений добиваются выполнения условия  .
.
Шаг 2. Выражение целевой функции только через свободные переменные. На этом шаге убеждаются в том, что целевая функция выражена только через свободные переменные. Если это не так, пользуясь соответствующими уравнениями системы ограничений, выражают целевую функцию только через свободные переменные, т.е. приводят ее к виду:  . Далее переходят к шагу 3.
. Далее переходят к шагу 3.
Шаг 3. Проверка решения на оптимальность. Составляется начальная симплекс–таблица. В левой колонке этой таблицы помещают базисные переменные, а в крайней правой колонке – свободные члены соответствующих уравнений системы ограничений. На пересечении i -ой строки и j -го столбца размещают коэффициент при j -ой переменной в i -ом ограничении. В последней отчеркнутой строке (L – строке) размещают коэффициент при j -ой переменной в целевой функции, взятый с противоположным знаком. В последнем столбце L –строки (т.е. в правом нижнем углу таблицы) помещают значение свободного члена целевой функции со своим знаком. Чаще всего этим значением оказывается нуль. Пример начальной симплекс–таблицы:
Для проверки решения на оптимальность просматривается последняя L – строка таблицы. Если коэффициенты, стоящие при свободных переменных неотрицательны, то полученное решение оптимально. Полученное решение единственно, если все эти коэффициенты строго положительны. Если среди неотрицательных коэффициентов при свободных переменных встречается хотя бы один нулевой, то задача имеет бесконечное множество решений. Если же в последней строке таблицы есть хотя бы один отрицательный коэффициент (при свободных переменных), а в соответствующем этому коэффициенту столбце нет ни одного положительного элемента, то целевая функция не ограничена на ОДР.
Наконец, если хотя бы один из коэффициентов, стоящих при свободных переменных, отрицательный и в соответствующем ему столбце есть хотя бы один положительный элемент, то полученное решение может быть улучшено. И можно переходить к шагу 4.
Шаг 4. Получение нового решения. Этот шаг условно может быть разделен на три более мелких шага.
Шаг 4.1. Выбор переменной, вводимой в список базисных переменных. Просматривается последняя строка симплекс – таблицы. Среди элементов этой строки выбирается максимальный по модулю отрицательный элемент. Столбец, в котором стоит этот элемент, называется разрешающим. Если, например, это p -ый столбец, то переменная 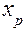 вводится в список базисных переменных.
вводится в список базисных переменных.
Шаг 4.2. Выбор переменной, выводимой из списка базисных переменных. Находят отношения элементов столбца свободных членов к элементам разрешающего столбца. При этом при делении на отрицательный, или нулевой элемент разрешающего столбца результат деления полагают равным +¥. Среди всех этих отношений находят минимальное. Строка, соответствующая минимальному отношению, называется разрешающей. Пусть, например, это q -ая строка, тогда базисная переменная  выводится из списка базисных переменных. Элемент симплекс – таблицы, стоящий на пересечении разрешающих строки и столбца называется разрешающим, в рассмотренном случае это будет элемент
выводится из списка базисных переменных. Элемент симплекс – таблицы, стоящий на пересечении разрешающих строки и столбца называется разрешающим, в рассмотренном случае это будет элемент  .
.
Шаг. 4.3. Выполнение симплекс – преобразования и переход к новой симплекс – таблице. Элемент  новой симплекс-таблицы вычисляется с помощью следующего симплекс – преобразования:
новой симплекс-таблицы вычисляется с помощью следующего симплекс – преобразования:

При проведении симплекс–преобразования весьма удобно пользоваться правилом треугольника:
Для получения элемента новой симплекс–таблицы надо от элемента предыдущей симплекс–таблицы, стоящего на том же месте, отнять следующее выражение: произведение элемента разрешающей строки, стоящего в одном столбце с данным элементом, на элемент данной строки, стоящий в одном столбце с разрешающим элементом, деленное на разрешающий элемент.
Таким образом, при переходе к новой симплекс–таблице все элементы разрешающей строки делятся на разрешающий элемент; все элементы разрешающего столбца, кроме разрешающего элемента, старой таблицы в новой таблице обнуляются, а все остальные элементы старой симплекс–таблицы, включая коэффициенты целевой функции и свободные члены, пересчитываются по соответствующей формуле с использованием правила треугольника.
Новое решение имеет следующую структуру: все свободные переменные в нем полагаются равными нулю, а все базисные переменные – свободным членам, стоящим в одной строке с ними. После построения новой симплекс–таблицы следует вернуться к выполнению шага 3.
ПРИМЕР: Найти оптимальное решение задачи линейного программирования заданной математической моделью вида:

Для решения этой задачи симплекс–методом необходимо привести ее к каноническому виду, добавив в левые части неравенств ограничений по одной дополнительной неотрицательной переменной:

Убедившись, что полученный вид модели является стандартным, приступаем к реализации алгоритма решения задачи симплекс– методом.
Шаг 1. Базисные переменные:  , а свободные:
, а свободные:  . При этом начальное решение имеет вид:
. При этом начальное решение имеет вид:  при этом
при этом 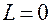 .
.
Шаг 2. Целевая функция уже выражена через свободные переменные.
Шаг 3. Составим начальную симплекс–таблицу (верхняя в каскаде таблиц):
| БП
| 
| 
| 
| 
| СЧ
|

| 1
| 0
| 1
| 0
| 4
|

| 0
| 1
| 0
| 1
| 2
|
| L
| -1
| -1
| 0
| 0
| 0
|

| 1
| 0
| 1
| 0
| 4
|

| 0
| 1
| 0
| 1
| 2
|
| L
| 0
| -1
| 1
| 0
| 4
|

| 1
| 0
| 1
| 0
| 4
|

| 0
| 1
| 0
| 1
| 2
|
| L
| 0
| 0
| 1
| 1
| 6
|
Просмотрев последнюю строку начальной таблицы, заключаем, что начальное решение не оптимально, т.к. L – строка этой таблицы содержит отрицательные числа в столбцах, соответствующих свободным переменным. Поэтому переходим к шагу 4.
Шаг 4. Поскольку L – строка начальной таблицы содержит два одинаковых отрицательных числа, то безразлично, какое из них выбирать. Выберем для определенности первое из этих чисел, тогда первый столбец будет разрешающим, а переменная  будет введена в список базисных.
будет введена в список базисных.
Подсчитав отношения:  , заключаем, что разрешающей становится первая строка, элемент
, заключаем, что разрешающей становится первая строка, элемент 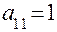 становится разрешающим элементом (он выделен в начальной таблице жирным шрифтом и подчеркнут), а переменная
становится разрешающим элементом (он выделен в начальной таблице жирным шрифтом и подчеркнут), а переменная  выводится из состава базисных переменных.
выводится из состава базисных переменных.
Составим теперь новую симплекс – таблицу, которая помещена ниже предыдущей, начальной таблицы, под общей «шапкой».
Замечание. На практике обычно для экономии места все симплекс – таблицы располагают ниспадающим каскадом, одна под другой, под общей верхней «шапкой».
Возвращаемся к шагу 3. Новое решение имеет вид:  , при этом
, при этом  , т.е. значение целевой функции возросло. Но это решение не оптимально, т.к. в столбце L – строки, соответствующем свободной переменной
, т.е. значение целевой функции возросло. Но это решение не оптимально, т.к. в столбце L – строки, соответствующем свободной переменной 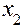 , имеется отрицательный элемент. При этом, не все остальные элементы этого столбца отрицательные, или нулевые, поэтому это решение может быть улучшено, и мы переходим к шагу 4.
, имеется отрицательный элемент. При этом, не все остальные элементы этого столбца отрицательные, или нулевые, поэтому это решение может быть улучшено, и мы переходим к шагу 4.
Разрешающим в этом случае будет второй столбец. Поскольку  , вторая строка будет разрешающей, а ее элемент
, вторая строка будет разрешающей, а ее элемент  разрешающим элементом (аналогично выделен во второй таблице). Учитывая эти результаты, составим новую, третью симплекс – таблицу и возвратимся к шагу 3.
разрешающим элементом (аналогично выделен во второй таблице). Учитывая эти результаты, составим новую, третью симплекс – таблицу и возвратимся к шагу 3.
Последнее решение имеет вид:  при этом
при этом  .
.
Это решение оптимально, т.к. все числа, стоящие в L –строке в столбцах свободных переменных неотрицательны. Это решение единственно, т.к. они строго положительны.
Итак, получено оптимальное решение задачи линейного программирования в виде:  .
.




 , выразив их через остальные (n – m) неизвестные.
, выразив их через остальные (n – m) неизвестные.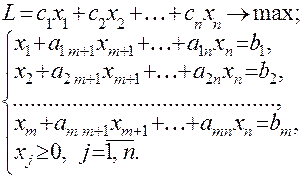
 (если это не так, то переменные всегда можно перенумеровать), тогда начальное решение будет иметь вид:
(если это не так, то переменные всегда можно перенумеровать), тогда начальное решение будет иметь вид:
 , то начальное решение является допустимым, и можно переходить к шагу 2. В противном случае повторяют алгоритм поиска начального решения, т.е. преобразованиями уравнений системы ограничений добиваются выполнения условия
, то начальное решение является допустимым, и можно переходить к шагу 2. В противном случае повторяют алгоритм поиска начального решения, т.е. преобразованиями уравнений системы ограничений добиваются выполнения условия  .
. . Далее переходят к шагу 3.
. Далее переходят к шагу 3.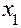




 …
…


 …
…
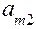

 …
…


 …
…




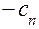
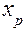 вводится в список базисных переменных.
вводится в список базисных переменных. выводится из списка базисных переменных. Элемент симплекс – таблицы, стоящий на пересечении разрешающих строки и столбца называется разрешающим, в рассмотренном случае это будет элемент
выводится из списка базисных переменных. Элемент симплекс – таблицы, стоящий на пересечении разрешающих строки и столбца называется разрешающим, в рассмотренном случае это будет элемент  .
. новой симплекс-таблицы вычисляется с помощью следующего симплекс – преобразования:
новой симплекс-таблицы вычисляется с помощью следующего симплекс – преобразования:


 , а свободные:
, а свободные:  . При этом начальное решение имеет вид:
. При этом начальное решение имеет вид:  при этом
при этом 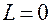 .
.



 будет введена в список базисных.
будет введена в список базисных. , заключаем, что разрешающей становится первая строка, элемент
, заключаем, что разрешающей становится первая строка, элемент 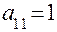 становится разрешающим элементом (он выделен в начальной таблице жирным шрифтом и подчеркнут), а переменная
становится разрешающим элементом (он выделен в начальной таблице жирным шрифтом и подчеркнут), а переменная  , при этом
, при этом  , т.е. значение целевой функции возросло. Но это решение не оптимально, т.к. в столбце L – строки, соответствующем свободной переменной
, т.е. значение целевой функции возросло. Но это решение не оптимально, т.к. в столбце L – строки, соответствующем свободной переменной 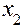 , имеется отрицательный элемент. При этом, не все остальные элементы этого столбца отрицательные, или нулевые, поэтому это решение может быть улучшено, и мы переходим к шагу 4.
, имеется отрицательный элемент. При этом, не все остальные элементы этого столбца отрицательные, или нулевые, поэтому это решение может быть улучшено, и мы переходим к шагу 4. , вторая строка будет разрешающей, а ее элемент
, вторая строка будет разрешающей, а ее элемент  разрешающим элементом (аналогично выделен во второй таблице). Учитывая эти результаты, составим новую, третью симплекс – таблицу и возвратимся к шагу 3.
разрешающим элементом (аналогично выделен во второй таблице). Учитывая эти результаты, составим новую, третью симплекс – таблицу и возвратимся к шагу 3. при этом
при этом  .
. .
.

