Теорема. Пусть заданные на одном и том же множестве функции  и
и  непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции 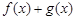 ,
,  ,
,  и
и  также непрерывны в точке
также непрерывны в точке  (частное при условии
(частное при условии  ).
).
Доказательство. Поскольку  и
и 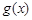 непрерывны в точке
непрерывны в точке  , то
, то  и
и  . Используя теорему о пределах функций, получим:
. Используя теорему о пределах функций, получим:
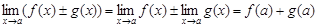 ,
,
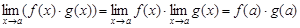 ,
,
 .
.
Следовательно, согласно определению 1, функции  ,
,  ,
, 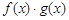 и
и  непрерывны в точке
непрерывны в точке  (частное при условии
(частное при условии  ).
).
Сложная функция и ее непрерывность
Последовательное применение двух или нескольких функций называется суперпозицией этих функций.
Функции, образованные в результате суперпозиции двух или нескольких функций будем называть сложными функциями. Например, сложная функция  образована в результате суперпозиции функций
образована в результате суперпозиции функций  и
и  . Достаточно определить сложную функцию, образованную в результате суперпозиции двух функций. Определение. Пусть функция
. Достаточно определить сложную функцию, образованную в результате суперпозиции двух функций. Определение. Пусть функция  определена на некотором множестве
определена на некотором множестве  и пусть
и пусть  - множество значений этой функции. Если на указанном множестве
- множество значений этой функции. Если на указанном множестве  определена другая функция
определена другая функция  , то говорят, что на множестве
, то говорят, что на множестве  задана сложная функция переменной
задана сложная функция переменной 
 .
.
Теорема. Если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция 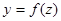 непрерывна в точке
непрерывна в точке  , соответствующей точке
, соответствующей точке  , то сложная функция
, то сложная функция 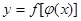 непрерывна в точке
непрерывна в точке  .
.
Доказательство. В силу непрерывности функции  в точке
в точке 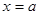 имеем:
имеем:  , то есть при
, то есть при  имеем
имеем  . Поэтому вследствии непрерывности функции
. Поэтому вследствии непрерывности функции  в точке
в точке  получаем
получаем  , то есть
, то есть  . Следовательно, предел функции
. Следовательно, предел функции  в точке
в точке  равен ее значению в этой точке
равен ее значению в этой точке  , что и доказывает непрерывность сложной функции
, что и доказывает непрерывность сложной функции 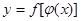 в точке
в точке  .
.
Обратная функция и ее непрерывность.
Определение. Функция  называется неубывающей (невозрастающей) на множестве
называется неубывающей (невозрастающей) на множестве  , если для любых
, если для любых  и
и  из этого множества, удовлетворяющих условию
из этого множества, удовлетворяющих условию  , справедливо неравенство
, справедливо неравенство  (
( ). Неубывающие и невозрастающие функции называются монотонными.
). Неубывающие и невозрастающие функции называются монотонными.
Определение. Функция  называется возрастающей (убывающей) на множестве
называется возрастающей (убывающей) на множестве  , если для любых
, если для любых  и
и  из этого множества, удовлетворяющих условию
из этого множества, удовлетворяющих условию  , справедливо неравенство
, справедливо неравенство  (
( ). Убывающие и возрастающие функции называются строго монотонными.
). Убывающие и возрастающие функции называются строго монотонными.
Определение. Пусть функция  задана на отрезке
задана на отрезке  , и пусть множеством значений этой функции является отрезок
, и пусть множеством значений этой функции является отрезок  . Пусть каждому значению
. Пусть каждому значению  из отрезка
из отрезка  ставится в соответствие по некоторому закону единственное значение
ставится в соответствие по некоторому закону единственное значение  из отрезка
из отрезка  , для которого
, для которого  . Тогда на отрезке
. Тогда на отрезке  можно определить функцию
можно определить функцию  , ставя в соответствие каждому
, ставя в соответствие каждому  из отрезка
из отрезка  , то значение
, то значение  из отрезка
из отрезка  , для которого
, для которого 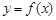 . Функция
. Функция  называется обратной для функции
называется обратной для функции  .
.
В этом определении вместо отрезков  и
и  можно рассматривать интервалы
можно рассматривать интервалы  и
и  или считать, что один или оба интервала превращаются в бесконечную прямую
или считать, что один или оба интервала превращаются в бесконечную прямую  или в открытую полупрямую
или в открытую полупрямую 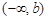 ,
,  .
.
Заметим, что если  - обратная функция для функции
- обратная функция для функции  , то функция
, то функция  - обратная функция для функции
- обратная функция для функции  . Функции
. Функции  и
и  называются взаимно обратными.
называются взаимно обратными.
Взаимно обратные функции обладают следующими очевидными свойствами:
 ,
,
 .
.
Пример. Рассмотрим на полупрямой  функцию
функцию  . Областью значений этой функции является полупрямая
. Областью значений этой функции является полупрямая  . каждому
. каждому 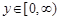 поставим в соответствие по формуле
поставим в соответствие по формуле  единственное значение
единственное значение  . Тогда
. Тогда  . Следовательно,
. Следовательно,  является обратной для функции
является обратной для функции  .
.
Пример. Рассмотрим на отрезке  функцию
функцию  . Областью значений этой функции является отрезок
. Областью значений этой функции является отрезок  . Обозначим через
. Обозначим через  угол, принадлежащий отрезку
угол, принадлежащий отрезку  , синус которого равен
, синус которого равен  . Тогда функция
. Тогда функция  будет обратной к данной. Действительно,
будет обратной к данной. Действительно,  .
.
Заметим, что при записи обратной функции независимую переменную нередко обозначают  , а значение функции
, а значение функции  , то есть пишут
, то есть пишут  . Например,
. Например,  - функция обратная для функции
- функция обратная для функции  . Функция
. Функция  - функция обратная для функции
- функция обратная для функции  .
.
Теорема. Пусть на отрезке  задана возрастающая (убывающая) непрерывная функция
задана возрастающая (убывающая) непрерывная функция  , и пусть
, и пусть  и
и  . Тогда эта функция имеет на отрезке
. Тогда эта функция имеет на отрезке  (
( ) возрастающую (убывающую) непрерывную обратную функцию
) возрастающую (убывающую) непрерывную обратную функцию  .
.



 и
и  непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции 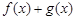 ,
,  ,
,  и
и  также непрерывны в точке
также непрерывны в точке  ).
). и
и 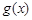 непрерывны в точке
непрерывны в точке  , то
, то  и
и  . Используя теорему о пределах функций, получим:
. Используя теорему о пределах функций, получим: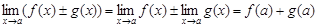 ,
,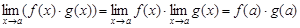 ,
, .
. ,
, 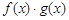 и
и  непрерывны в точке
непрерывны в точке  образована в результате суперпозиции функций
образована в результате суперпозиции функций  и
и  . Достаточно определить сложную функцию, образованную в результате суперпозиции двух функций. Определение. Пусть функция
. Достаточно определить сложную функцию, образованную в результате суперпозиции двух функций. Определение. Пусть функция  определена на некотором множестве
определена на некотором множестве  и пусть
и пусть  - множество значений этой функции. Если на указанном множестве
- множество значений этой функции. Если на указанном множестве  определена другая функция
определена другая функция  , то говорят, что на множестве
, то говорят, что на множестве 
 .
. непрерывна в точке
непрерывна в точке  , а функция
, а функция 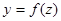 непрерывна в точке
непрерывна в точке  , соответствующей точке
, соответствующей точке  , то сложная функция
, то сложная функция 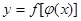 непрерывна в точке
непрерывна в точке  .
. в точке
в точке 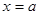 имеем:
имеем:  , то есть при
, то есть при  имеем
имеем  . Поэтому вследствии непрерывности функции
. Поэтому вследствии непрерывности функции  получаем
получаем  , то есть
, то есть  . Следовательно, предел функции
. Следовательно, предел функции  в точке
в точке  равен ее значению в этой точке
равен ее значению в этой точке  , что и доказывает непрерывность сложной функции
, что и доказывает непрерывность сложной функции 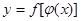 в точке
в точке  , если для любых
, если для любых  и
и  из этого множества, удовлетворяющих условию
из этого множества, удовлетворяющих условию  , справедливо неравенство
, справедливо неравенство  (
( ). Неубывающие и невозрастающие функции называются монотонными.
). Неубывающие и невозрастающие функции называются монотонными. называется возрастающей (убывающей) на множестве
называется возрастающей (убывающей) на множестве  (
( ). Убывающие и возрастающие функции называются строго монотонными.
). Убывающие и возрастающие функции называются строго монотонными. задана на отрезке
задана на отрезке  , и пусть множеством значений этой функции является отрезок
, и пусть множеством значений этой функции является отрезок  . Пусть каждому значению
. Пусть каждому значению  из отрезка
из отрезка  ставится в соответствие по некоторому закону единственное значение
ставится в соответствие по некоторому закону единственное значение  из отрезка
из отрезка  , для которого
, для которого  . Тогда на отрезке
. Тогда на отрезке  можно определить функцию
можно определить функцию  , ставя в соответствие каждому
, ставя в соответствие каждому  из отрезка
из отрезка  , то значение
, то значение  из отрезка
из отрезка 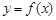 . Функция
. Функция  называется обратной для функции
называется обратной для функции  и
и  или считать, что один или оба интервала превращаются в бесконечную прямую
или считать, что один или оба интервала превращаются в бесконечную прямую  или в открытую полупрямую
или в открытую полупрямую 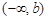 ,
,  .
. - обратная функция для функции
- обратная функция для функции  , то функция
, то функция  и
и  ,
, .
. функцию
функцию  . Областью значений этой функции является полупрямая
. Областью значений этой функции является полупрямая  . каждому
. каждому 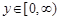 поставим в соответствие по формуле
поставим в соответствие по формуле  единственное значение
единственное значение  . Тогда
. Тогда  . Следовательно,
. Следовательно,  .
. функцию
функцию  . Областью значений этой функции является отрезок
. Областью значений этой функции является отрезок  . Обозначим через
. Обозначим через  угол, принадлежащий отрезку
угол, принадлежащий отрезку  , синус которого равен
, синус которого равен  . Тогда функция
. Тогда функция  будет обратной к данной. Действительно,
будет обратной к данной. Действительно,  .
. , а значение функции
, а значение функции  . Например,
. Например,  - функция обратная для функции
- функция обратная для функции  . Функция
. Функция  - функция обратная для функции
- функция обратная для функции  .
. задана возрастающая (убывающая) непрерывная функция
задана возрастающая (убывающая) непрерывная функция  , и пусть
, и пусть  и
и  . Тогда эта функция имеет на отрезке
. Тогда эта функция имеет на отрезке  (
( ) возрастающую (убывающую) непрерывную обратную функцию
) возрастающую (убывающую) непрерывную обратную функцию  .
.

