

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В процессе счета сначала возникает так называемый натуральный ряд чисел  Множество этих чисел называется множеством натуральных чисел и обозначается
Множество этих чисел называется множеством натуральных чисел и обозначается 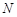 ={
={  }. Далее в арифметике вводятся операции сложения, вычитания, умножения и деления. Однако в результате вычитания или деления не всегда получаются натуральные числа, и возникает необходимость расширить класс рассматриваемых чисел.
}. Далее в арифметике вводятся операции сложения, вычитания, умножения и деления. Однако в результате вычитания или деления не всегда получаются натуральные числа, и возникает необходимость расширить класс рассматриваемых чисел.
Вводятся число 0 и отрицательные числа - 1, - 2, …,- n, … Натуральные числа, число 0 и указанные отрицательные числа образуют множество целых чисел 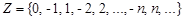 . Очевидно, что множество натуральных чисел является подмножеством целых чисел, то есть
. Очевидно, что множество натуральных чисел является подмножеством целых чисел, то есть  .
.
При делении целых чисел появляются рациональные числа вида 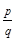 , где
, где 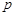 и
и  - целые числа, причем
- целые числа, причем  . Множество рациональных чисел обозначают буквой
. Множество рациональных чисел обозначают буквой  . Его можно записать в виде
. Его можно записать в виде  . Рациональное число
. Рациональное число 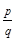 , вообще говоря, можно записать не единственным образом. Например,
, вообще говоря, можно записать не единственным образом. Например,  Чтобы избежать этой неопределенности говорят, что рациональное число - это несократимая обыкновенная дробь. При этом предполагают, что если числитель и знаменатель имеют общие множители, то дробь следует сократить. Заметим также, что целые числа также представимы в виде
Чтобы избежать этой неопределенности говорят, что рациональное число - это несократимая обыкновенная дробь. При этом предполагают, что если числитель и знаменатель имеют общие множители, то дробь следует сократить. Заметим также, что целые числа также представимы в виде 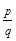 , если положить
, если положить  . Следовательно,
. Следовательно,  .
.
В процессе измерения геометрических величин выяснилось, что длина отрезка не всегда может быть задана рациональным числом. Таким примером может служить длина гипотенузы прямоугольного треугольника с катетами, равными 1. Как следует из теоремы Пифагора, длина гипотенузы в данном треугольнике равна 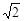 . Предположим, что
. Предположим, что 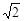 - рациональное число, то есть может быть представлено в виде
- рациональное число, то есть может быть представлено в виде 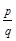 . Причем
. Причем 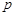 и
и  не имеют общих множителей. После возведения в квадрат равенства
не имеют общих множителей. После возведения в квадрат равенства 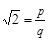 получим
получим  или
или
|
|
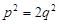 . (1)
. (1)
Последнее равенство означает, что  - четное число. Тогда
- четное число. Тогда  также является четным и может быть записано в виде
также является четным и может быть записано в виде  .
.  Подставляя
Подставляя 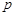 в (1) получим
в (1) получим  . Отсюда следует, что
. Отсюда следует, что  - тоже четное число. Но в этом случае
- тоже четное число. Но в этом случае 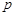 и
и  имеют общий множитель, равный двум, а мы предположили, что
имеют общий множитель, равный двум, а мы предположили, что 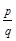 - несократимая дробь. Следовательно, наше предположение оказалось неверным, и
- несократимая дробь. Следовательно, наше предположение оказалось неверным, и  не является рациональным числом. Итак, извлечение корня, вычисление логарифмов, значений тригонометрических функций и прочие операции привели к появлению иррациональных чисел. Все рациональные и иррациональные числа образуют множество вещественных (действительных) чисел. Множество вещественных чисел обозначают
не является рациональным числом. Итак, извлечение корня, вычисление логарифмов, значений тригонометрических функций и прочие операции привели к появлению иррациональных чисел. Все рациональные и иррациональные числа образуют множество вещественных (действительных) чисел. Множество вещественных чисел обозначают  . Очевидно, справедливо соотношение
. Очевидно, справедливо соотношение  .
.
Любое вещественное число может быть представлено бесконечной десятичной дробью. При этом рациональные числа можно представить в виде:
) бесконечной десятичной периодической дроби, то есть дроби, у которой, начиная с некоторого знака, одна или несколько последующих цифр периодически повторяются, например,  (эти повторяющиеся цифры записывают в круглых скобках).
(эти повторяющиеся цифры записывают в круглых скобках).
) либо в виде конечной десятичной дроби. Отметим также, что рациональные числа, имеющие вид конечной десятичной дроби 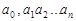 , допускают двоякое представление в виде бесконечной десятичной дроби. Во-первых, такую дробь можно считать бесконечной, у которой все знаки с номерами большими
, допускают двоякое представление в виде бесконечной десятичной дроби. Во-первых, такую дробь можно считать бесконечной, у которой все знаки с номерами большими  равны нулю, то есть представить ее в виде
равны нулю, то есть представить ее в виде  . Так
. Так  можно записать как 0,5000…=0,5 (0), а 1= 1.000. =1. (0). Или такую конечную десятичную дробь
можно записать как 0,5000…=0,5 (0), а 1= 1.000. =1. (0). Или такую конечную десятичную дробь 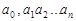 можно записать в виде
можно записать в виде
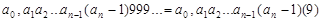 .
.
И тогда  а 1 = 1.000. =1. (0) =0,999…=0, (9).
а 1 = 1.000. =1. (0) =0,999…=0, (9).
Далее мы всегда будем использовать вторую форму записи.
Иррациональные числа всегда представляются бесконечной десятичной непериодической дробью.
Очевидно, что имеет место следующее включение множеств  .
.
Числовые последовательности
Определение. Если каждому натуральному числу 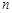 ставится в соответствие по определенному закону некоторое вещественное число
ставится в соответствие по определенному закону некоторое вещественное число 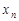 , то совокупность занумерованных чисел
, то совокупность занумерованных чисел 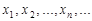 называют числовой последовательностью или просто последовательностью.
называют числовой последовательностью или просто последовательностью.
|
|
Числа 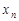 называются элементами или членами последовательности. По своему определению последовательность содержит бесконечное множество элементов. Последовательность с элементами
называются элементами или членами последовательности. По своему определению последовательность содержит бесконечное множество элементов. Последовательность с элементами 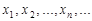 обозначают также {
обозначают также { 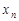 }.
}.
Например, 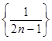 - это последовательность
- это последовательность 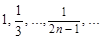 ,
,
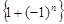 - это последовательность 0, 2, 0, 2, …
- это последовательность 0, 2, 0, 2, …
Последовательность может быть задана с помощью формулы 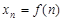 , которая называется формулой общего члена последовательности. Например, формула
, которая называется формулой общего члена последовательности. Например, формула  задает последовательность
задает последовательность 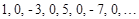
Суммой (разностью) двух последовательностей 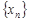 и
и 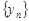 называется последовательность
называется последовательность 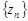 , все элементы которой равны сумме (разности)
, все элементы которой равны сумме (разности) 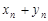 (
(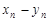 ).
).
Произведением двух последовательностей 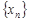 и
и 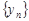 называется последовательность
называется последовательность 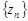 =
= 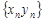 , частным - последовательность
, частным - последовательность 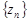 =
= 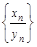 , причем при определении частного нужно потребовать, чтобы все элементы последовательности
, причем при определении частного нужно потребовать, чтобы все элементы последовательности 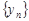 были отличны от нуля.
были отличны от нуля.
Ограниченные и неограниченные последовательности
Определение. Последовательность 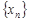 называется ограниченной сверху (снизу), если найдется такое вещественное число
называется ограниченной сверху (снизу), если найдется такое вещественное число 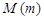 , что для всех членов последовательности справедливо неравенство
, что для всех членов последовательности справедливо неравенство 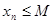 (
(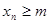 ).
).
Последовательность 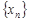 называется ограниченной, если она ограничена и сверху и снизу, т.е. если найдутся такие вещественные числа
называется ограниченной, если она ограничена и сверху и снизу, т.е. если найдутся такие вещественные числа 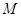 и
и 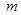 , что для всех членов последовательности справедливо неравенство
, что для всех членов последовательности справедливо неравенство 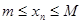 .
.
Это определение можно сформулировать по другому:
Последовательность 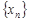 называется ограниченной, если найдется положительное число
называется ограниченной, если найдется положительное число 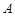 такое, что для всех членов последовательности справедливо неравенство
такое, что для всех членов последовательности справедливо неравенство 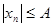 . (Здесь
. (Здесь 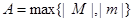 ).
).
Последовательность 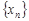 называется неограниченной, если для любого положительного числа
называется неограниченной, если для любого положительного числа 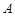 найдется хотя бы один элемент последовательности, удовлетворяющий неравенству
найдется хотя бы один элемент последовательности, удовлетворяющий неравенству 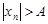 .
.
Примеры.1. 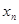 =
= 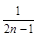 - ограниченная последовательность, так как
- ограниченная последовательность, так как 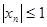 .
.
. 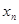 =
= 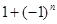 - ограниченная последовательность, так как
- ограниченная последовательность, так как 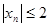 .
.
. 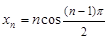 - неограниченная последовательность {
- неограниченная последовательность { 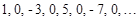 }, так как для любого положительного числа
}, так как для любого положительного числа 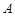 найдется хотя бы один элемент последовательности, удовлетворяющий неравенству
найдется хотя бы один элемент последовательности, удовлетворяющий неравенству 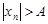 .
.
Бесконечно большие и бесконечно малые последовательности
Определение. Последовательность 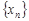 называется бесконечно большой, если для любого положительного числа
называется бесконечно большой, если для любого положительного числа 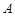 найдется номер
найдется номер 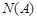 , зависящий от
, зависящий от 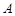 , такой, что для всех номеров
, такой, что для всех номеров 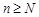 справедливо неравенство
справедливо неравенство 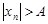 .
.
|
|
Пример. Последовательность 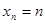 , то есть последовательность натуральных чисел {
, то есть последовательность натуральных чисел { 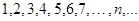 } является бесконечно большой, так как для любого положительного числа
} является бесконечно большой, так как для любого положительного числа 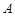 найдется номер
найдется номер 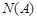 , такой, что для всех номеров
, такой, что для всех номеров 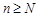 справедливо неравенство
справедливо неравенство 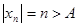 .
.
Очевидно, что любая бесконечно большая последовательность является неограниченной. Действительно, для того, чтобы последовательность была неограниченной необходимо, чтобы для любого положительного числа 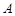 неравенство
неравенство 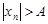 выполнялось, хотя бы для одного элемента последовательности, но из определения бесконечно большой последовательности следует, что такими элементами являются все элементы последовательности, начиная с некоторого номера
выполнялось, хотя бы для одного элемента последовательности, но из определения бесконечно большой последовательности следует, что такими элементами являются все элементы последовательности, начиная с некоторого номера 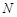 .
.
Обратное утверждение неверно, то есть неограниченная последовательность не всегда является бесконечно большой.
Пример. Рассмотрим последовательность 0, 2, 0, 4, …, у которой все члены с нечетными номерами равны нулю, а члены с четными номерами 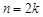
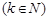 равны
равны 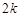 . Поскольку для любого положительного числа
. Поскольку для любого положительного числа 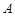 найдется натуральное число
найдется натуральное число 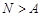 , то для четных номеров
, то для четных номеров 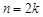 больших
больших 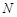 справедливо неравенство
справедливо неравенство 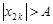 . Следовательно, данная последовательность является неограниченной. Однако она не является бесконечно большой, так как, какой бы большой номер
. Следовательно, данная последовательность является неограниченной. Однако она не является бесконечно большой, так как, какой бы большой номер 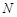 мы не взяли, имеются члены с нечетными номерами
мы не взяли, имеются члены с нечетными номерами 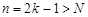 , равные нулю, для которых неравенство
, равные нулю, для которых неравенство 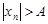 не имеет места.
не имеет места.
Определение. Последовательность 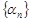 называется бесконечно малой, если для любого положительного числа
называется бесконечно малой, если для любого положительного числа 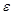 найдется номер
найдется номер 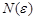 , зависящий от
, зависящий от 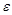 , такой, что при
, такой, что при 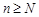 все элементы
все элементы 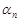 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству 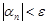 .
.
Пример. Показать, что последовательность 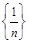 является бесконечно малой.
является бесконечно малой.
Пусть 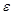 - произвольное положительное число. Тогда
- произвольное положительное число. Тогда 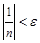 при всех
при всех 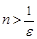 , то есть за номер
, то есть за номер 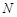 можно принять натуральное число
можно принять натуральное число 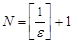 , где
, где 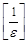 - целая часть числа
- целая часть числа 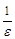 . Поскольку для произвольного числа
. Поскольку для произвольного числа 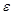 мы смогли определить номер
мы смогли определить номер 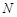 такой, что при всех
такой, что при всех 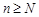 справедливо неравенство
справедливо неравенство 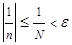 , то последовательность
, то последовательность 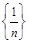 - бесконечно малая.
- бесконечно малая.
Пример. Показать, что последовательность 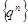 является бесконечно большой, если
является бесконечно большой, если 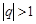 , и бесконечно малой, если
, и бесконечно малой, если 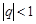 .
.
) Пусть 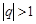 . Возьмем произвольное положительное число
. Возьмем произвольное положительное число 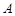 . Тогда
. Тогда 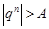 , при всех
, при всех 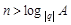 . Возьмем
. Возьмем 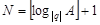 . Тогда для всех
. Тогда для всех 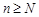 справедлива цепочка неравенств
справедлива цепочка неравенств 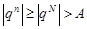 . Следовательно, последовательность
. Следовательно, последовательность 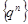 является бесконечно большой.
является бесконечно большой.
|
|
) Если 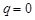 , то для любого положительного числа
, то для любого положительного числа 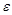 и любого номера
и любого номера 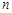 выполняется неравенство
выполняется неравенство 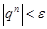 , и последовательность
, и последовательность 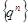 - бесконечно малая. Рассмотрим случай
- бесконечно малая. Рассмотрим случай 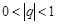 . В этом случае
. В этом случае 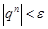 , при всех
, при всех 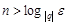 . Возьмем
. Возьмем 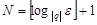 . Тогда при всех
. Тогда при всех 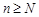
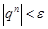 . Следовательно, если
. Следовательно, если 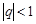 , то последовательность
, то последовательность 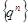 является бесконечно малой.
является бесконечно малой.
Предел числовой последовательности. Сходящиеся последовательности
Определение 1. Число 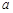 называется пределом последовательности
называется пределом последовательности 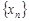 , если для любого положительного числа
, если для любого положительного числа 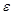 найдется такой номер
найдется такой номер 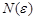 , зависящий от
, зависящий от 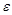 , что при
, что при 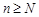 все элементы
все элементы 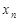 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству
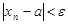 . (1)
. (1)
Символически это записывают так
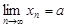 , или
, или 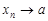 при
при 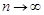 .
.
Неравенство (1) означает, что, начиная с номера 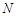 , все элементы последовательности находятся внутри интервала
, все элементы последовательности находятся внутри интервала 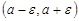 , который называют
, который называют 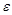 -окрестностью числа
-окрестностью числа 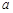 .
.
Согласно данному определению бесконечно малая последовательность 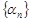 имеет своим пределом нуль, то есть
имеет своим пределом нуль, то есть 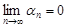 .
.
Если последовательность 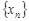 является бесконечно большой, то пишут
является бесконечно большой, то пишут 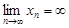 . В случае бесконечно большой последовательности, все члены которой, начиная с некоторого номера положительны, говорят, что ее предел равен
. В случае бесконечно большой последовательности, все члены которой, начиная с некоторого номера положительны, говорят, что ее предел равен 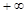 и пишут
и пишут 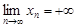 . Если же все члены бесконечно большой последовательности, начиная с некоторого номера отрицательны, то ее предел считают равным
. Если же все члены бесконечно большой последовательности, начиная с некоторого номера отрицательны, то ее предел считают равным 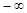 и пишут
и пишут 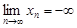 .
.
Определение 2. Число  называется пределом последовательности
называется пределом последовательности 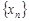 , если в любой
, если в любой 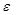 -окрестности числа
-окрестности числа  находятся все элементы данной последовательности, начиная с некоторого номера.
находятся все элементы данной последовательности, начиная с некоторого номера.
Последнее утверждение означает, что, если число  - предел последовательности, то за пределами любой его
- предел последовательности, то за пределами любой его 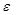 -окрестности находится лишь конечное число элементов данной последовательности.
-окрестности находится лишь конечное число элементов данной последовательности.
Определение. Последовательность 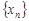 называется сходящейся, если она имеет конечный предел. Если предел не существует или равен
называется сходящейся, если она имеет конечный предел. Если предел не существует или равен 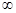 , то последовательность называется расходящейся.
, то последовательность называется расходящейся.
Из определения 2 следует, что последовательность расходится, если для любого числа  найдется его
найдется его 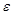 -окрестность, за пределами которой лежит бесконечное число элементов последовательности.
-окрестность, за пределами которой лежит бесконечное число элементов последовательности.
Пример 1. Рассмотрим последовательность 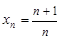 . Покажем, что
. Покажем, что 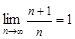 .
.
Пусть 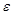 - произвольное положительное число. Тогда неравенство
- произвольное положительное число. Тогда неравенство 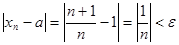 выполняется при всех
выполняется при всех 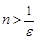 , то есть за номер
, то есть за номер 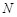 можно принять натуральное число
можно принять натуральное число 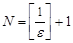 , где
, где 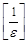 - целая часть числа
- целая часть числа 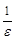 . Поскольку для произвольного числа
. Поскольку для произвольного числа 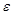 мы смогли определить номер
мы смогли определить номер 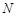 такой, что при всех
такой, что при всех 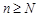 справедливо неравенство
справедливо неравенство 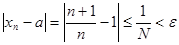 , то последовательность
, то последовательность 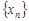 сходится, а ее предел равен единице, то есть
сходится, а ее предел равен единице, то есть 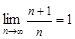 .
.
Пример 2. Последовательность 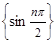 расходится.
расходится.
Действительно, данная последовательность - это последовательность 1, 0, - 1, 0, 1, 0, - 1, … Пусть 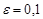 . Если, число
. Если, число  принадлежит интервалу
принадлежит интервалу 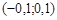 , то в
, то в 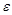 -окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или - 1, окажутся за пределами
-окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или - 1, окажутся за пределами 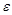 -окрестности. Если число
-окрестности. Если число  принадлежит интервалу (0,9; 1,1) или (-1,1; - 0,9), то за пределами
принадлежит интервалу (0,9; 1,1) или (-1,1; - 0,9), то за пределами 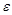 -окрестности заведомо окажутся все нулевые члены последовательности. При всех остальных значениях числа
-окрестности заведомо окажутся все нулевые члены последовательности. При всех остальных значениях числа  в его
в его 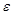 -окрестность не попадет ни одного члена последовательности. Итак какое бы число
-окрестность не попадет ни одного члена последовательности. Итак какое бы число  мы не взяли, для заданного
мы не взяли, для заданного 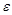 найдется бесконечное число элементов последовательности, не принадлежащих
найдется бесконечное число элементов последовательности, не принадлежащих 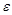 -окрестности числа
-окрестности числа  . Следовательно, рассматриваемая последовательность расходится.
. Следовательно, рассматриваемая последовательность расходится.
|
|
Основные свойства сходящихся последовательностей.
Теорема 1. Сходящаяся последовательность имеет только один предел.
Доказательство. ( Методом от противного). Предположим, что последовательность 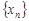 сходится и имеет два разных предела, то есть
сходится и имеет два разных предела, то есть 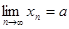 и
и 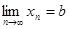 , причем
, причем 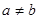 . Возьмем
. Возьмем 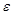 -окрестность числа а, которая не содержит b. Так как а - предел последовательности
-окрестность числа а, которая не содержит b. Так как а - предел последовательности 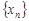 , то по определению 2 за пределами
, то по определению 2 за пределами 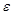 -окрестности находится лишь конечное число элементов данной последовательности и, следовательно, число b не может быть ее пределом.
-окрестности находится лишь конечное число элементов данной последовательности и, следовательно, число b не может быть ее пределом.
Теорема 2. Если все элементы последовательности равны одному и тому же числу 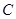 , то и предел такой последовательности также равен числу
, то и предел такой последовательности также равен числу 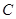 , то есть, если
, то есть, если 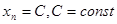 , то и
, то и 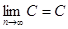 .
.
Доказательство. Рассмотрим последовательность 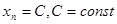 . Покажем, что
. Покажем, что 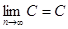 , то есть предел последовательности равен константе
, то есть предел последовательности равен константе 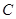 . Рассмотрим любую
. Рассмотрим любую 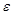 -окрестность числа С. Все члены последовательности попадут в эту окрестность, а за ее пределами не окажется ни одного члена последовательности. Согласно определению 2 это и означает, что число С есть предел данной последовательности.
-окрестность числа С. Все члены последовательности попадут в эту окрестность, а за ее пределами не окажется ни одного члена последовательности. Согласно определению 2 это и означает, что число С есть предел данной последовательности.
Теорема 3. Сумма, разность, произведение и частное двух сходящихся последовательностей 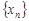 и
и 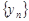 (частное при условии, что предел
(частное при условии, что предел 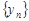 отличен от нуля) есть сходящаяся последовательность, предел которой равен соответственно сумме, разности, произведению и частному пределов последовательностей
отличен от нуля) есть сходящаяся последовательность, предел которой равен соответственно сумме, разности, произведению и частному пределов последовательностей 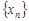 и
и 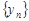 , то есть, если
, то есть, если
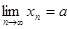 ,
, 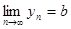 , то
, то
) 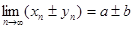 ;
;
) 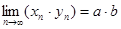 ;
;
) 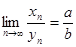 ,
, 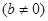 .
.
Доказательство. Докажем свойство 1) для суммы двух сходящихся последовательностей, то есть докажем, что 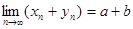 . Возьмем любое положительное число
. Возьмем любое положительное число 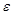 . Поскольку
. Поскольку 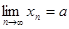 , то для положительного числа
, то для положительного числа 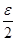 существует номер
существует номер 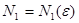 такой, что при всех
такой, что при всех 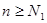 выполняется неравенство
выполняется неравенство 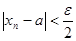 . Аналогично, так как
. Аналогично, так как 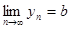 то для положительного числа
то для положительного числа 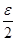 существует номер
существует номер 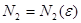 такой, что при всех
такой, что при всех 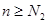 выполняется неравенство
выполняется неравенство 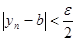 . Обозначим
. Обозначим 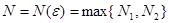 . Тогда при всех
. Тогда при всех 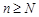 справедливо
справедливо
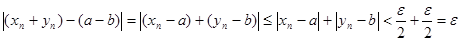 .
.
Это и означает, что 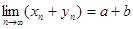 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Постоянный множитель можно выносить за знак предела, то есть
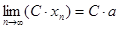 , где
, где 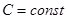 .
.
Теорема 4. Сходящаяся последовательность ограничена.
Теорема 5. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.
То есть, если 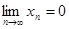 , а последовательность {
, а последовательность { 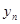 } - ограниченная, то
} - ограниченная, то 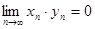 .
.
Доказательство. Пусть { 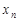 } - бесконечно малая, а {
} - бесконечно малая, а { 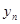 } - ограниченная последовательности. Требуется доказать, что последовательность
} - ограниченная последовательности. Требуется доказать, что последовательность 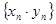 - бесконечно малая последовательность. Так как {
- бесконечно малая последовательность. Так как { 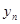 } - ограниченная, то существует положительное число
} - ограниченная, то существует положительное число 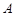 такое, что для всех членов последовательности справедливо неравенство
такое, что для всех членов последовательности справедливо неравенство 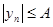 . Возьмем любое положительное число
. Возьмем любое положительное число 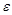 . Поскольку {
. Поскольку { 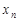 } - бесконечно малая, то для положительного числа
} - бесконечно малая, то для положительного числа 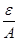 существует номер
существует номер 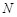 такой, что при всех
такой, что при всех 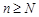 выполняется неравенство
выполняется неравенство 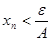 . Тогда при всех
. Тогда при всех 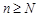 справедливо
справедливо
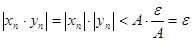 .
.
Это означает, что последовательность 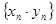 - бесконечно малая.
- бесконечно малая.
Пример. Последовательность 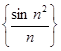 - бесконечно малая как произведение ограниченной последовательности
- бесконечно малая как произведение ограниченной последовательности 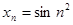 и бесконечно малой
и бесконечно малой 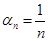 . Следовательно,
. Следовательно, 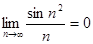 .
.
Теорема 6. Если последовательность { 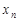 } - бесконечно большая, то, начиная с некоторого номера, определена последовательность
} - бесконечно большая, то, начиная с некоторого номера, определена последовательность 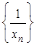 , которая является бесконечно малой. Если все элементы бесконечно малой последовательности
, которая является бесконечно малой. Если все элементы бесконечно малой последовательности 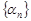 не равны нулю, то последовательность
не равны нулю, то последовательность 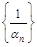 - бесконечно большая.
- бесконечно большая.
(Без доказательства).
Теорема 7 (о трех последовательностях). Пусть последовательности 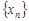 и
и 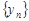 сходятся и имеют общий предел
сходятся и имеют общий предел  , то есть
, то есть  . Пусть, кроме того, начиная с некоторого номера, элементы последовательности
. Пусть, кроме того, начиная с некоторого номера, элементы последовательности  удовлетворяют неравенствам
удовлетворяют неравенствам  . Тогда последовательность
. Тогда последовательность  также сходится и имеет предел
также сходится и имеет предел  , то есть
, то есть 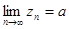 .
.
Предельные точки последовательности
Определение. Точка  бесконечной прямой называется предельной точкой последовательности
бесконечной прямой называется предельной точкой последовательности 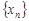 , если в любой
, если в любой 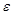 -окрестности этой точки имеется бесконечно много элементов последовательности
-окрестности этой точки имеется бесконечно много элементов последовательности 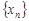 .
.
Предельные точки называют также частичными пределами последовательности.
Пример. Найти все предельные точки последовательности  .
.
Данная последовательность - это последовательность 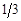 , 3,
, 3, 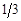 , 3, …
, 3, …
По определению последовательность 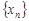 имеет две предельные точки: 1/3 и 3. Покажем, что других предельных точек у данной последовательности нет. Пусть
имеет две предельные точки: 1/3 и 3. Покажем, что других предельных точек у данной последовательности нет. Пусть  - произвольная точка числовой оси, отличная от 1/3 и 3. Выберем число
- произвольная точка числовой оси, отличная от 1/3 и 3. Выберем число 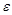 достаточно малым для того, чтобы
достаточно малым для того, чтобы 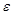 -окрестности точек
-окрестности точек  , 1/3 и 3 не пересекались. Тогда все элементы последовательности находятся в
, 1/3 и 3 не пересекались. Тогда все элементы последовательности находятся в 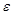 -окрестности точек, 1/3 и 3, а в
-окрестности точек, 1/3 и 3, а в 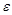 -окрестности точки
-окрестности точки  нет ни одного элемента. Согласно определению точка
нет ни одного элемента. Согласно определению точка  не является предельной точкой.
не является предельной точкой.
Определение. Наибольшая предельная точка (наибольший частичный предел) последовательности называется верхним пределом этой последовательности и обозначается символом  . Наименьшая предельная точка (наименьший частичный предел) последовательности называется нижним пределом этой последовательности и обозначается символом
. Наименьшая предельная точка (наименьший частичный предел) последовательности называется нижним пределом этой последовательности и обозначается символом 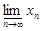 .
.
Функция
Понятие функции
Определение. Если каждому значению переменной  из некоторого множества
из некоторого множества  ставится в соответствие по известному закону единственное число
ставится в соответствие по известному закону единственное число 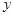 , то говорят, что на множестве
, то говорят, что на множестве  задана функция
задана функция  или
или  .
.
При этом  называется аргументом функции, множество
называется аргументом функции, множество 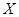 - областью задания функции
- областью задания функции  . Число
. Число  , которое соответствует данному значению аргумента
, которое соответствует данному значению аргумента  , называется частным значением функции в точке
, называется частным значением функции в точке  . Совокупность всех частных значений образует вполне определенное множество
. Совокупность всех частных значений образует вполне определенное множество  , называемое множеством значений функции.
, называемое множеством значений функции.
Функция  называется четной (нечетной), если для любого
называется четной (нечетной), если для любого  из области определения функции справедливо равенство
из области определения функции справедливо равенство  (
( ).
).
Функция  называется периодической, если существует такое число
называется периодической, если существует такое число  , что для любого
, что для любого  из области определения функции справедливо равенство
из области определения функции справедливо равенство 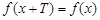 . Наименьшее из чисел
. Наименьшее из чисел  называют периодом функции.
называют периодом функции.
Функции могут задаваться, например, при помощи формул. Такой способ называется аналитическим. В этом случае используется некоторый запас изученных и специально обозначенных функций и алгебраические действия.
Например, 
 ,
, 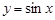 ,
,  и т.д. Иногда на разных участках своей области задания функции задаются разными формулами. Например, функция
и т.д. Иногда на разных участках своей области задания функции задаются разными формулами. Например, функция  , которая принимает значение, равное 1 при
, которая принимает значение, равное 1 при  , 0 при
, 0 при 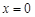 , - 1 при
, - 1 при  может быть записана следующим образом
может быть записана следующим образом
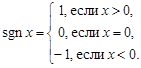
Название функции  произошло от латинского слова signum - знак. Областью задания этой функции является вся числовая прямая, а область значений состоит из трех чисел: 1, 0, - 1.
произошло от латинского слова signum - знак. Областью задания этой функции является вся числовая прямая, а область значений состоит из трех чисел: 1, 0, - 1.
Функция может быть также задана с помощью описания соответствия. Например, поставим в соответствие вещественному числу  наибольшее целое не превосходящее
наибольшее целое не превосходящее  . В результате получим функцию, определенную на всей числовой оси, и принимающей целочисленные значения. Эту функцию называют целой частью числа
. В результате получим функцию, определенную на всей числовой оси, и принимающей целочисленные значения. Эту функцию называют целой частью числа  и обозначают
и обозначают 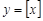 . Другим примером может служить функция Дирихле, принимающая значение, равное 1, если
. Другим примером может служить функция Дирихле, принимающая значение, равное 1, если  - рациональное число и 0, если
- рациональное число и 0, если  - иррациональное число.
- иррациональное число.
Еще один способ задания функции - это табличный способ. В этом случае для некоторых значений переменной  указывают соответствующие значения функции. Данные таблиц могут быть получены как непосредственно из опыта, так и с <
указывают соответствующие значения функции. Данные таблиц могут быть получены как непосредственно из опыта, так и с <
|
|
|

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!