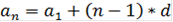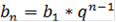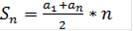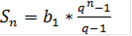Определение самой длинной арифметической прогрессии

Оглавление

 

Введение

Понятие прогрессии

Постановка задачи

Определение самой длинной арифметической прогрессии

Определение самой длинной геометрической прогрессии

Формирование самой длинной прогрессии

Дополнительные возможности

Функциональная блок-схема

Формирование последовательности

Определение самой длинной арифметической прогрессии

Поиск самой длинной геометрической прогрессии

Формирование самой длинной прогрессии

Полный текст программы

Скриншоты

Введение

Условие задачи: в заданной целочисленной последовательности найти такую подпоследовательность, которая является арифметической или геометрической прогрессией. Поиск прогрессии будет осуществляться в среде Delphi.

Для начала нужно задать последовательность. Это можно сделать различными способами: ввод с клавиатуры, чтение из файла, генерирование случайных чисел. В данной задаче последовательность будет задаваться случайным образом.

Дальнейшей задачей является нахождение самой длинной прогрессии. Для этого нужно найти все возможные прогрессии, сравнить количества элементов всех прогрессий между собой и вывести самую длинную из них. То есть придется сравнить все числа между собой при различных разностях и знаменателях прогрессий. Причем нужно учесть, что первым элементом прогрессии может быть любой из элементов последовательности, что усложняет задачу. Для решения этой задачи будут использоваться программирование вложенных циклов, генератор случайных чисел, работа с динамическими массивами, работа с процедурами и т. д..

Понятие прогрессии

 

Под прогрессией понимают подмножество множества рациональных чисел, обладающих общей разностью (знаменателем) прогрессии. Разность (знаменатель) прогрессии - это показатель, показывающий, какую зависимость между собой имеют члены прогрессии.

Различают арифметические и геометрические прогрессии. Арифметическая прогрессия - это прогрессия, в которой каждый последующий член прогрессии отличается от предыдущего на значение, равное разности этой прогрессии. Геометрическая прогрессия - это прогрессия, в которой отношение любого члена этой прогрессии к предыдущему члену равно знаменателю прогрессии. Общие формулы для нахождения n-ного члена таких прогрессий выглядят так:

 

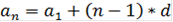
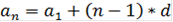 - для арифметической прогрессии,

 

где a₁ - первый член прогрессии, d - разность прогрессии;

 

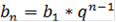
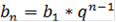 - для геометрической прогрессии,

 

где b₁ - первый член прогрессии, q - знаменатель прогрессии.

Также можно находить сумму первых n членов таких прогрессий:

 

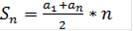
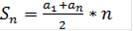, для арифметической прогрессии;

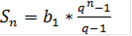
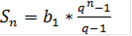, для геометрической прогрессии.

 

Постановка задачи

 

Итак, рассмотрим конкретную задачу. Дана последовательность хаотично-расположенных натуральных чисел. Из этой последовательности требуется выделить самую длинную прогрессию, независимо от того, арифметическая она или геометрическая.

Для начала определим последовательность чисел. Количество элементов (n) последовательности будет задаваться с клавиатуры. После этого генерируется последовательность (P) элементы которой лежат на отрезке [-n; n]. Итак, определена некоторая последовательность P.

Теперь можно приступить к поиску прогрессии.

 

Дополнительные возможности

 

Дополнительными возможностями будет являться то, что можно будет вывести самую длинную прогрессию определенного типа.

Для этого достаточно осуществить определение только арифметической, или геометрической, прогрессии и затем сформировать ее. Не придется сравнивать длины самых длинных прогрессий, а просто найти их по отдельности, что даже упрощает задачу.

Функциональная блок-схема

 

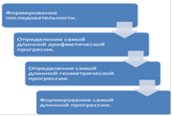
последовательность прогрессия программа delphi

Формирование последовательности.

 

procedure TForm1.posledovatelnost(var P: massiv);n,i:integer;;strtoint(edit1.Text)<250 then:=strtoint(edit1.Text):=250;(P,n);i:=0 to n-1 do begin[i]:=random(n+1)-random(n+1);book1.NumberRC[3,i+2]:=P[i] end;

P - последовательность;

N - длина последовательности.

Полный текст программы

 

unit Unit1;

interface, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, Menus, AxCtrls, OleCtrls, VCF1, StdCtrls, Math, OleCtnrs,, jpeg;=array of integer;= class(TForm): TMainMenu;: TEdit;: TLabel;Book1: TF1Book;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;: TOleContainer;: TLabel;: TImage;arithmetic_progression(var P: massiv;max_kol, max_num, max_dx: integer);geometric_progression(var P: massiv;max_kol, max_num, max_dx: integer);formirovanie(var P, R:massiv;max_kol, max_num, max_dx, progression_type: integer);posledovatelnost(var P:massiv);N1Click(Sender: TObject);N2Click(Sender: TObject);N3Click(Sender: TObject);N4Click(Sender: TObject);N5Click(Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm1;

{$R *.dfm}

////////////////////////////////////////////////////////////////////////////////

{ Определение арифметической прогрессии.}

procedure TForm1.arithmetic_progression(var P: massiv;max_kol, max_num, max_dx: integer);i,j,x,dx,kol:integer;:boolean;dx:=1 to high(P) doi:=0 to high(P) do begin:=P[i];:=0;:=0;P[j]=x+dx then begin(kol);:=x+dx;:=true endbegin:=false;(j) end;(b=true) or (j=high(P));j=high(P);kol>max_kol then begin_kol:=kol;_num:=i;_dx:=dx end end;;

////////////////////////////////////////////////////////////////////////////////

{Формирование самой длинной прогрессии.}

procedure TForm1.formirovanie(var P, R: massiv;max_kol, max_num, max_dx, progression_type: integer);x,j:integer;:boolean;:=P[max_num];(R,1);[0]:=x;book1.NumberRC[6,2]:=R[0];:=false;progression_type of

: beginbook1.TextRC[7,11]:=’Разность’+inttostr(max_dx);1book1.TextRC[5,11]:=’Арифметическая прогрессия’;

repeat

j:=0;

repeatP[j]=x+max_dx then begin:=x+max_dx;(R,length(R)+1);[high(R)]:=x;book1.NumberRC[6,length(R)+1]:=R[high(R)];:=true endbegin:=false;(j) end(b=true) or (j=high(P));j=high(P) end;

: beginbook1.TextRC[7,11]:=’Знаменатель’+inttostr(max_dx);1book1.TextRC[5,11]:=’Геометрическая прогрессия.’;

repeat:=0;(P[j]=x*max_dx) and (j<>max_num) then begin:=x*max_dx;(R,length(R)+1);[high(R)]:=x;book1.NumberRC[6,length(R)+1]:=R[high(R)];:=true endbegin:=false;(j) end(b=true) or (j=high(P));j=high(P) end;

////////////////////////////////////////////////////////////////////////////////

{Определение самой длинной геометрической прогрессии.}

procedure TForm1.geometric_progression(var P:massiv;max_kol, max_num, max_dx: integer);i,j,x,dx,kol:integer;:boolean;dx:=-high(P) to high(P) doi:=0 to high(P) doP[i]<>0 then begin:=P[i];:=1;(dx>1) or (dx<-1) then begin:=0;(P[j]=x*dx) and (j<>i) then begin(kol);:=x*dx;:=true endbegin:=false;(j) end;(b=true) or (j=high(P));j=high(P);kol>max_kol then begin_kol:=kol;_num:=i;_dx:=dx end end end;;

////////////////////////////////////////////////////////////////////////////////

{Формирование самой длинной арифметической прогрессии.}

procedure TForm1.N1Click(Sender: TObject);P,R:massiv;_kol,max_num,max_dx,i,y,progression_type:integer;i:=1 to 2 dobook1.ClearRange(3*i,2,3*i,256,3);_kol:=0;_num:=0;_dx:=0;(P);_progression(P,max_kol,max_num,max_dx);_type:=1;(P,R,max_kol,max_num,max_dx,progression_type);

////////////////////////////////////////////////////////////////////////////////

{Формирование самой длинной геометрической прогрессии.}

procedure TForm1.N2Click(Sender: TObject);P,R:massiv;_kol,max_num,max_dx,i,y,progression_type:integer;i:=1 to 2 dobook1.ClearRange(3*i,2,3*i,256,3);_kol:=0;_num:=0;_dx:=0;(P);_progression(P,max_kol,max_num,max_dx);_type:=2;(P,R,max_kol,max_num,max_dx,progression_type);

////////////////////////////////////////////////////////////////////////////////

{Формирование самой длинной арифметической или геометрической, в зависимости от случая, прогрессии}

procedure TForm1.N3Click(Sender: TObject);P,R:massiv;_kol,max_num,max_dx,i,y,progression_type:integer;i:=1 to 2 dobook1.ClearRange(3*i,2,3*i,256,3);_kol:=0;_num:=0;_dx:=0;(P);_progression(P,max_kol,max_num,max_dx);:=max_kol;_progression(P,max_kol,max_num,max_dx);y<max_kol then_type:=2_type:=1;(P,R,max_kol,max_num,max_dx,progression_type);

////////////////////////////////////////////////////////////////////////////////

{Очистка результатов.}TForm1.N4Click(Sender: TObject);book1.ClearRange(3,2,3,256,3);book1.ClearRange(6,2,6,256,3);book1.ClearRange(8,2,10,4,3);.Clear;

////////////////////////////////////////////////////////////////////////////////

{Закрытие программы.}TForm1.N5Click(Sender: TObject);

form1.Close

end;

////////////////////////////////////////////////////////////////////////////////

{Формирование последовательности.}

procedure TForm1.posledovatelnost(var P: massiv);n,i:integer;:boolean;;strtoint(edit1.Text)<250 then:=strtoint(edit1.Text):=250;(P,n);i:=0 to n-1 do begin[i]:=random(n+1)-random(n+1);book1.NumberRC[3,i+2]:=P[i] end

end;

////////////////////////////////////////////////////////////////////////////////.

 

Скриншоты

 

Основной вид программы.

 

Меню

 

Найдена арифметическая прогрессия

 

Найдена геометрическая прогрессия

Заключение

 

Проделав весь этот долгий путь, мы пришли к тому, что можем выделить из любой последовательности самую длинную арифметическую прогрессию, самую длинную геометрическую прогрессию и самую длинную прогрессию из всех арифметических и геометрических прогрессий.

Можно было бы предложить несколько иной способ выполнения поставленной задачи: сформировать самые длинные арифметическую и геометрическую прогрессию, сравнить их между собой и вывести самую длинную из них. Но, в целях того, чтобы не находить лишнее а программе, был использован предложенный выше подход.

Таким образом, можно считать что с поставленной задачей мы справились полностью.

Список литературы

v Фаронов В.В. DELPHI. Программирование на языке высокого уровня. Учебник для вузов. СПб, Питер, 2003.

v Сухарев М. Delphi. Полное руководство. Включая версию 2010. СПб.: Наука и техника, 2010.

v Иванова Г.С. Технология программирования: Учебник для вузов. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.

v Киммел П. Создание приложений в Delphi. М.: Издат. Дом «Вильямс», 2003.

v Далахвелидзе П.Г., Марков Е.П. Разработка Web-служб средствами Delphi. СПб, БХВ-Петербург, 2003.

Оглавление

 

Введение

Понятие прогрессии

Постановка задачи

Определение самой длинной арифметической прогрессии

Определение самой длинной геометрической прогрессии

Формирование самой длинной прогрессии

Дополнительные возможности

Функциональная блок-схема

Формирование последовательности

Определение самой длинной арифметической прогрессии

Поиск самой длинной геометрической прогрессии

Формирование самой длинной прогрессии

Полный текст программы

Скриншоты

Введение

Условие задачи: в заданной целочисленной последовательности найти такую подпоследовательность, которая является арифметической или геометрической прогрессией. Поиск прогрессии будет осуществляться в среде Delphi.

Для начала нужно задать последовательность. Это можно сделать различными способами: ввод с клавиатуры, чтение из файла, генерирование случайных чисел. В данной задаче последовательность будет задаваться случайным образом.

Дальнейшей задачей является нахождение самой длинной прогрессии. Для этого нужно найти все возможные прогрессии, сравнить количества элементов всех прогрессий между собой и вывести самую длинную из них. То есть придется сравнить все числа между собой при различных разностях и знаменателях прогрессий. Причем нужно учесть, что первым элементом прогрессии может быть любой из элементов последовательности, что усложняет задачу. Для решения этой задачи будут использоваться программирование вложенных циклов, генератор случайных чисел, работа с динамическими массивами, работа с процедурами и т. д..

Понятие прогрессии

 

Под прогрессией понимают подмножество множества рациональных чисел, обладающих общей разностью (знаменателем) прогрессии. Разность (знаменатель) прогрессии - это показатель, показывающий, какую зависимость между собой имеют члены прогрессии.

Различают арифметические и геометрические прогрессии. Арифметическая прогрессия - это прогрессия, в которой каждый последующий член прогрессии отличается от предыдущего на значение, равное разности этой прогрессии. Геометрическая прогрессия - это прогрессия, в которой отношение любого члена этой прогрессии к предыдущему члену равно знаменателю прогрессии. Общие формулы для нахождения n-ного члена таких прогрессий выглядят так:

 

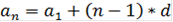
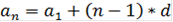 - для арифметической прогрессии,

 

где a₁ - первый член прогрессии, d - разность прогрессии;

 

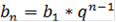
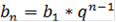 - для геометрической прогрессии,

 

где b₁ - первый член прогрессии, q - знаменатель прогрессии.

Также можно находить сумму первых n членов таких прогрессий:

 

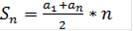
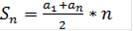, для арифметической прогрессии;

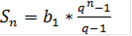
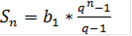, для геометрической прогрессии.

 

Постановка задачи

 

Итак, рассмотрим конкретную задачу. Дана последовательность хаотично-расположенных натуральных чисел. Из этой последовательности требуется выделить самую длинную прогрессию, независимо от того, арифметическая она или геометрическая.

Для начала определим последовательность чисел. Количество элементов (n) последовательности будет задаваться с клавиатуры. После этого генерируется последовательность (P) элементы которой лежат на отрезке [-n; n]. Итак, определена некоторая последовательность P.

Теперь можно приступить к поиску прогрессии.

 

Определение самой длинной арифметической прогрессии

 

Начнем с того, что выберем разность прогрессии. Он, фактически, лежит в пределах [-n; n]. Пусть разностью прогрессии является некоторое число dx>0. Этой разности соответствует некоторая возрастающая прогрессия. Выберем другую разность прогрессии, равную -dx. Очевидно, что этой разности соответствует некоторая убывающая прогрессия, причем первый элемент этой прогрессии равен последнему элементу прогрессии, разность которой равна dx, а последний элемент этой прогрессии равен первому элементу прогрессии, разность которой равна dx. Следовательно, интервал изменения разности прогрессии можно сузить до [0; n]. Значение разности прогрессии, равное нулю, также отбросим, т. к. при поиске каждого последующего члена прогрессии мы будем приходить к одному и тому же элементу последовательности. Такая прогрессия будет обладать бесконечной длиной. Итак, разность прогрессии лежит в пределах [1; n]. Будем искать прогрессии при n различных разностях прогрессий. Будем считать, что мы выбрали некоторую разность прогрессии равную dx.

Далее нужно выбрать первый член прогрессии. В качестве первого члена прогрессии может служить любой из элементов последовательности. Нужно перепробовать все элементы P_i последовательности P, где 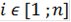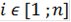. Примем один из элементов последовательности за первый член прогрессии и обозначим x.

Теперь нужно определить длину этой прогрессии. Пусть kol - длина прогрессии. Ее начальное значение равно 1, т. к. мы уже имеем первый элемент прогрессии x. Теперь, начиная с первого, будем сравнивать x c остальными элементами последовательности до тех пор, пока не найдется элемент, отличающийся от x на величину dx. Этот элемент будет являться вторым элементом прогрессии. То есть kol уже равен 2. Теперь x примет значение второго члена прогрессии. Далее будем сравнивать второй член прогрессии с остальными элементами последовательности, до тех пор, пока не найдется третий элемент прогрессии. Этот процесс будет продолжаться до тех пор, пока при одном и том же x не переберем все элементы последовательности. Когда сравним x_kol со всеми остальными элементами последовательности и среди них не окажется следующего члена прогрессии, то установившееся значение kol будет длиной этой прогрессии.

Введем еще одну переменные max_kol (длина самой длинной прогрессии), max_num (номер, соответствующий элементу последовательности, выбранного за первый элемент самой длинной прогрессии), max_dx (разность самой длинной прогрессии). Присвоим значения: max_kol:=kol, max_num:=i, max_dx:=dx.

Примем за первый член прогрессии следующий элемент последовательности и проделаем все действия описанные выше. Получим новое значение kol. Если оно больше чем max_kol, то max_kol:=kol, max_num:=i, max_dx:=dx.

Нужно проделать все это, пока в качестве первого члена прогрессии не выступит каждый элемент последовательности. Затем нужно поменять dx и повторять все, пока не переберем все значения dx. В конце получаем значение длины самой длинной арифметической прогрессии. Присвоим это значение переменной y, т. к. при поиске самой длинной геометрической прогрессии, величина max_kol примет значение длины самой длинной геометрической прогрессии, а для дальнейшего сравнения этих длин, нужно сохранить значение длины самой длинной арифметической прогрессии.