

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пусть Р = (Р, +, ·, -, 0, 1)- поле скаляров. А - 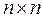 матрица.
матрица.
 -алгебраическое дополнение элемента
-алгебраическое дополнение элемента  .
.
Определение. Присоединённой к матрице А называется матрица

Теорема. Если  , то матрица А – обратима и
, то матрица А – обратима и 
Доказательство. Если  , то по теореме 2 п.3 матрица А обратима.
, то по теореме 2 п.3 матрица А обратима.
Рассмотрим матрицу  , обозначим
, обозначим 
Имеем 
Значит матрица 
Доказали что  , то есть
, то есть  значит
значит  . ■
. ■
Пример 1. Вычислить обратную матрицу с помощью присоединённой матрицы, то есть по формуле:  , где А=
, где А=  .
.
Решение. 
Вычислим определитель матрицы и алгебраические дополнения элементов матрицы.
 =-1
=-1




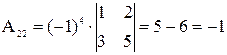




Тогда присоединённая матрица  =
= 

Пример2.  . Для данной матрицы второго порядка,
. Для данной матрицы второго порядка,
вывести формулу для вычисления  с помощью присоединённой матрицы.
с помощью присоединённой матрицы.
Ответ:  .
.
Пример 3.
Найти обратную матрицу  , используя формулу:
, используя формулу: 
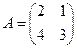 .
.
Решение.
Вычислим определитель матрицы:
 ,
,
Найдем присоединенную матрицу по формуле:
 , где
, где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  .
.
 .
.
Тогда
 .
.
Пример 4. Найти обратную матрицу  , используя формулу:
, используя формулу:  ,
,
 .
.
Решение. Найдем определитель матрицы:
 ;
;
Вычислим алгебраические дополнения:
 ;
; 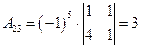 ;
;
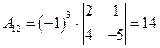 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
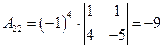 ;
;
Тогда
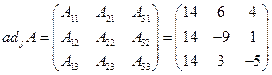 .
.
Следовательно
 .
.
Пример 5. Найти обратную матрицу  , используя формулу:
, используя формулу:  ,
,

Решение. Найдем определитель матрицы:
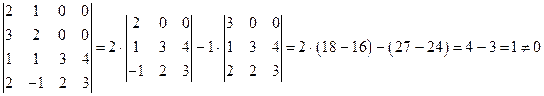 ;
;
 ;
;  ;
;
 ;
;  ;
;
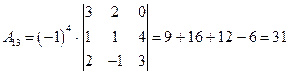 ;
; 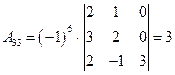 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
; 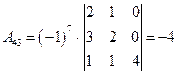 ;
;
 ;
;  ;
;
|
|
 ;
;
 .
.
Для самостоятельного решения.
Найти обратную матрицу  , используя формулу:
, используя формулу: 
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 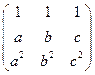 ;
;
7)  ; 8)
; 8) 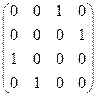 ;
;
9) 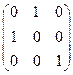 ;
;
10)  11)
11)  ;
;
12)  ; 13)
; 13)  ;
;
П.5. Решение матричных уравнений.
Теорема.  ;
;
 ;
;
 .
.
Пример1. Решить матричные уравнения вида AX = B:
 .
.
Решение.  ;
;
Вычислим  :
: 

 ,
,
Тогда 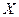 :
:
 .
.
Для самостоятельного решения:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
6)  ;
;
7)  ; 8)
; 8)  ;
; 
9)  ;
;
10)  .
.
Пример 2.  Решить матричные уравнения вида
Решить матричные уравнения вида 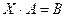 :
:
 .
.
Решение.  ,
,

 ,
,

 .
. 
Для самостоятельного решения:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ;
;
6)  ;
;
7) 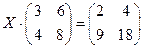 .
.
Пример 3. Решить матричные уравнения вида  :
:
1)  ;
;
Решение.
 .
.
1) 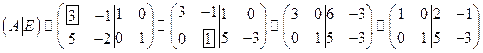


 ,
,



 ,
,
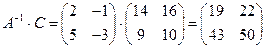 ,
,
 .
.
2)  .
.
Решение.



 ,
,



 ,
,
 ,
,
 .
.
Для самостоятельного решения:
3)  ;
;
4)  ;
;
5)  ;
;
6)  .
.
П.6. Записи решения системы n-линейных уравнений с n неизвестными в матричной форме.
Рассмотрим систему:


 ,
,  ,
,  - вектор-столбец.
- вектор-столбец.
Теорема 1. Если строки матрицы А линейно независимы, то система (1) имеет единственное решение:  .
.
Доказательство. Рассмотрим

 Систему (1) можно записать в матричной форме:
Систему (1) можно записать в матричной форме:

Так как строки матрицы А линейно независимы, то матрица А обратима:  . ■
. ■
Определение. Уравнение  называется матричной формой записи системы уравнений (1).
называется матричной формой записи системы уравнений (1).
Пример 1. Решить систему уравнений методом обратной матрицы:


Решение.
 -основная матрица,
-основная матрица,  .
.
Систему (3) можно записать в виде: 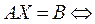
 .
.
 ; А - обратима, поэтому
; А - обратима, поэтому  =
= 



 =
= 
 =
=  ;
;  =
=  ;
;  =
=  , где
, где


Ответ:  =
=  .
.
Пример 2.. Решить систему уравнений методом обратной матрицы:


Решение.
|
|
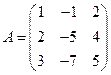 ,
,  ,
,  .
.
Запишем систему (4) матричной форме: 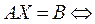
 =
= 
 =
= 
 ;
; 

Ответ: 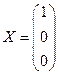 .
.
■
П.7. Правило Крамера.
Пусть Р = (Р, +, ·, -, 0, 1)- поле скаляров.

 ;
;
 ;
;
 -столбец свободных членов.
-столбец свободных членов.
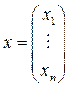
 - алгебраическое дополнение
- алгебраическое дополнение  .
. 
Теорема 1. Если определитель матрицы А не равен нулю, то система (1) имеет единственное решение, которое задаётся равенствами:


где матрица  получена из матрицы А заменой i -ого столбца столбцом свободных членов.
получена из матрицы А заменой i -ого столбца столбцом свободных членов.
Доказательство. Запишем систему (1) в матричной форме:
 ; по условию
; по условию  , значит матрица А – обратима, тогда
, значит матрица А – обратима, тогда 
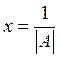
 .
.  =
= 
Формулы (2) называются формулами Крамера. ■
Пример 1. Найти решение системы по правилу Крамера.


 ,
,  .
.
 ,
, 
 ,
, 
Ответ: 
Пример 2. Решить системы уравнений по правилу Крамера:
1) 
Решение.
1) Найдем определитель системы:
 Вычислим определители, заменяя столбцом свободных членов поочередно столбцы основного определителя:
Вычислим определители, заменяя столбцом свободных членов поочередно столбцы основного определителя:
 ;
;
 ;
;
 ;
;
 ;
;

Получим  .
.
Ответ: 
Для самостоятельного решения 2) – 5).
2) 
3) 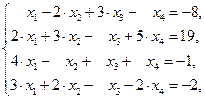
4) 
5) 
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!