Дифференциал обладает свойствами, аналогичными свойствам производной:

Формулы 1 – 4 получаются из соответствующих формул для производной умножением обеих частей каждого равенства на 
Рассмотрим дифференциал сложной функции. Пусть y сложная функция x:  Дифференциал
Дифференциал  этой функции, используя формулу для производной сложной функции, можно записать в виде
этой функции, используя формулу для производной сложной функции, можно записать в виде
 .
.
Но  есть дифференциал функции u, поэтому
есть дифференциал функции u, поэтому  т. е.
т. е.

Здесь дифференциал записан в том же виде, как и в формуле для дифференциала функции независимой переменной x, т. е.  хотя аргумент u является не независимой переменной, а функцией x.
хотя аргумент u является не независимой переменной, а функцией x.
Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называется инвариантностью (неизменностью) формы дифференциала.
С формально-технической точки зрения найти дифференциал функции – это «почти то же самое, что найти производную».
Пример.
Найти дифференциал функции 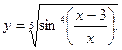
Решение. Перед тем, как находить производную или дифференциал, всегда целесообразно посмотреть, а нельзя ли как-нибудь упростить функцию (или запись функции) ещё до дифференцирования? В данном случае можно преобразовать корень и выполнить почленное деление аргумента синуса:
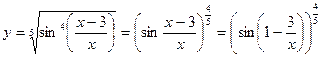
Функция сложная. Найдем производную, используя правило дифференцирования сложной функции два раза:
 Запишем дифференциал, при этом снова представим
Запишем дифференциал, при этом снова представим  в первоначальном виде:
в первоначальном виде:
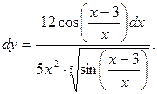
Когда производная представляет собой дробь, значок  обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
Применение дифференциала в приближенных вычислениях.
Выше было показано, что приращение функции представимо в виде:
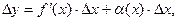 где функция
где функция 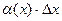 является бесконечно малой функцией при стремлении аргумента
является бесконечно малой функцией при стремлении аргумента 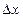 к нулю. Так как
к нулю. Так как  то
то 
В силу того, что второе слагаемое 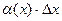 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому 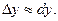
А так как нахождение дифференциал значительно проще, чем нахождение приращения функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:

Пример. Вычислить приближенно arctg 1,02, заменяя приращение функции ее дифференциалом.
Решение. Рассмотрим функцию  Необходимо вычислить ее значение в точке
Необходимо вычислить ее значение в точке  . Представим данное значение в виде следующей суммы:
. Представим данное значение в виде следующей суммы:  Величины
Величины 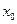 и
и  выбираются так, чтобы в точке
выбираются так, чтобы в точке 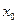 можно было бы достаточно легко вычислить значение функции и ее производной, а
можно было бы достаточно легко вычислить значение функции и ее производной, а 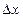 было бы достаточно малой величиной. С учетом этого, делаем вывод, что
было бы достаточно малой величиной. С учетом этого, делаем вывод, что  т.е.
т.е. 
Вычислим значение функции  в точке
в точке  .
.
Далее продифференцируем рассматриваемую функцию и найдем значение в точке 

Итак, 





 Дифференциал
Дифференциал  этой функции, используя формулу для производной сложной функции, можно записать в виде
этой функции, используя формулу для производной сложной функции, можно записать в виде .
. есть дифференциал функции u, поэтому
есть дифференциал функции u, поэтому  т. е.
т. е.
 хотя аргумент u является не независимой переменной, а функцией x.
хотя аргумент u является не независимой переменной, а функцией x.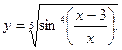
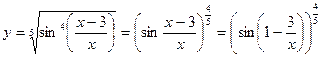
 Запишем дифференциал, при этом снова представим
Запишем дифференциал, при этом снова представим  в первоначальном виде:
в первоначальном виде: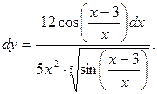
 обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).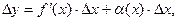 где функция
где функция 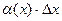 является бесконечно малой функцией при стремлении аргумента
является бесконечно малой функцией при стремлении аргумента 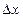 к нулю. Так как
к нулю. Так как  то
то 
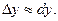

 Необходимо вычислить ее значение в точке
Необходимо вычислить ее значение в точке  . Представим данное значение в виде следующей суммы:
. Представим данное значение в виде следующей суммы:  Величины
Величины 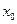 и
и  выбираются так, чтобы в точке
выбираются так, чтобы в точке 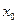 можно было бы достаточно легко вычислить значение функции и ее производной, а
можно было бы достаточно легко вычислить значение функции и ее производной, а  т.е.
т.е. 
 .
.





