Раздел 3. Дифференциальное исчисление.
Тема3.1 Производная функции
Определение производной
Для решения многих задач требуется найти разность значений функции в двух точках. Так, средняя скорость материальной точки за промежуток времени Δt равна:
 .
.
Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть:
 .
.
Рассмотрим поведение графика функции y=sinx в окрестности точки x=0. Если увеличивать масштаб графика, то кривизна графика становится все меньше и меньше, а сам график приближается к графику прямой y=x.
Эти и другие задачи приводят к понятию производной.
Пусть функция y=f(x) определена в некоторой окрестности точки х0 и существует конечный предел отношения
 при Δ x→0. Тогда этот предел называется производной функции в точке х0 : при Δ x→0. Тогда этот предел называется производной функции в точке х0 :
 Производная функции y=f(x) может также обозначаться одним из следующих способов:
Производная функции y=f(x) может также обозначаться одним из следующих способов:

| 
|
В физике производную по времени t часто обозначают точкой: 
Если приращение функции f(x0+Δx)–f(x0) обозначить как Δ y, то определение можно записать так:

Из определения производной и предела функции следует, что  , где α (Δ x) – бесконечно малая функция при Δ x →0.
, где α (Δ x) – бесконечно малая функция при Δ x →0.
Операция вычисления производной называется дифференцированием. Функция называется дифференцируемой в данной точке, если в этой точке существует ее производная.
Правила дифференцирования
Если C — постоянное число и  — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
— некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

Производная сложной функции
Сложная функция (композиция функций) записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом (если функций больше, то промежуточным аргументом) для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна
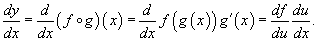
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
Производные элементарных функций
Таблица производных функций, аргументом которой является функция.
Производные высшего порядка
Пусть y = f (x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как

Примеры.
а) Найти производную сложной функции  .
.
Решение.
Здесь мы имеем дело с композицией трех функций, из которых внешней является тангенс. Производная тангенса равна 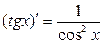
Тогда

б) Продифференцировать функцию 
Решение.
Сначала найдем производную произведения:

Далее, по формуле производной сложной функции

в) Определить производную функции 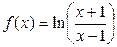 .
.
Решение.
Применим формулы производной сложной функции и производной частного.

г) Найти y'', если  .
.
Решение.
Возьмем первую производную дифференцируя функцию как произведение.

Теперь найдем производную второго порядка

д) Вычислить производную степенно-показательной функции

Решение.
Прологарифмируем заданную функцию:
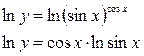
Вычислим производную, воспользовавшись формулой производной произведения и производной сложной функции:
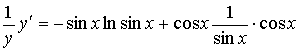
Выразим производную заданной функции:
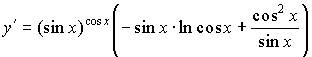 .
.
е) Вычислить производную функции с помощью логарифмического дифференцирования
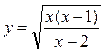 .
.
Решение.
Прологарифмируем функцию:

Преобразуем выражение с помощью свойств логарифмов:
 ;
;
Продифференцируем полученное равенство

 .
.
Выразим производную заданной функции:
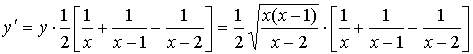 .
.
Раздел 3. Дифференциальное исчисление.
Тема3.1 Производная функции
Определение производной
Для решения многих задач требуется найти разность значений функции в двух точках. Так, средняя скорость материальной точки за промежуток времени Δt равна:
 .
.
Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть:
 .
.
Рассмотрим поведение графика функции y=sinx в окрестности точки x=0. Если увеличивать масштаб графика, то кривизна графика становится все меньше и меньше, а сам график приближается к графику прямой y=x.
Эти и другие задачи приводят к понятию производной.
Пусть функция y=f(x) определена в некоторой окрестности точки х0 и существует конечный предел отношения
 при Δ x→0. Тогда этот предел называется производной функции в точке х0 : при Δ x→0. Тогда этот предел называется производной функции в точке х0 :
 Производная функции y=f(x) может также обозначаться одним из следующих способов:
Производная функции y=f(x) может также обозначаться одним из следующих способов:

| 
|
В физике производную по времени t часто обозначают точкой: 
Если приращение функции f(x0+Δx)–f(x0) обозначить как Δ y, то определение можно записать так:

Из определения производной и предела функции следует, что  , где α (Δ x) – бесконечно малая функция при Δ x →0.
, где α (Δ x) – бесконечно малая функция при Δ x →0.
Операция вычисления производной называется дифференцированием. Функция называется дифференцируемой в данной точке, если в этой точке существует ее производная.



 .
. .
. при Δ x→0. Тогда этот предел называется производной функции в точке х0 :
при Δ x→0. Тогда этот предел называется производной функции в точке х0 :
 Производная функции y=f(x) может также обозначаться одним из следующих способов:
Производная функции y=f(x) может также обозначаться одним из следующих способов:




 , где α (Δ x) – бесконечно малая функция при Δ x →0.
, где α (Δ x) – бесконечно малая функция при Δ x →0. — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
— некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

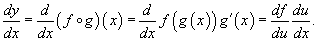





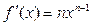


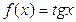
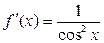
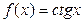


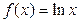

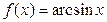







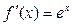
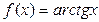



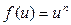





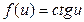



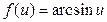


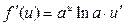










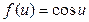




 .
.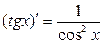




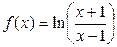 .
.
 .
.


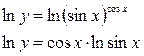
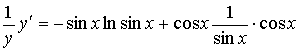
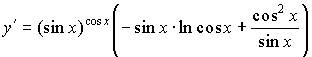 .
.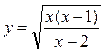 .
.
 ;
;
 .
.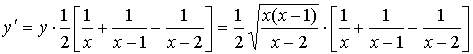 .
.


