

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
Топ:
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
(15 неделя, 1 час)
Алгоритмы вида «разделяй и властвуй» обеспечивают компактный и мощный инструмент решения различных задач; в этом параграфе мы займемся не столько разработкой подобных алгоритмов, сколько их анализом. При подсчете числа сравнений в циклах нам достаточно подсчитать число сравнений в одной итерации цикла и умножить его на число итераций. Этот подсчет становится сложнее, если число итераций внутреннего цикла зависит от параметров внешнего.
Подсчет итераций алгоритмов вида «разделяй и властвуй» не очень прост: он зависит от рекурсивных вызовов, от подготовительных и завершающих действий. Обычно неочевидно, сколько раз выполняется та или иная функция при рекурсивных вызовах. В качестве примера рассмотрим следующий алгоритм вида «разделяй и властвуй».
| DivideAndConquer(data,N,solution) | |
| data | набор входных данных |
| N | количество значений в наборе |
| solution | решение задачи |
| if (N <= SizeLimit) then | |
| DirectSolution(data,N,solution) | |
| else | |
| DivideInput(data.N,smallerSets,smallerSizes,numberSmaller) | |
| for i=l to numberSmaller do | |
| DivideAndConquer(smallerSets[i],smallerSizes[i],smallSol[i]) | |
| end for | |
| CombineSolutions(smallSol,numberSmaller,solution) | |
| end if | |
Этот алгоритм сначала проверяет, не мал ли размер задачи настолько, чтобы решение можно было найти с помощью простого нерекурсивного алгоритма (названного в тексте DirectSolution). и если это так, то происходит его вызов. Если задача слишком велика, то сначала вызывается процедура Dividelnput, которая разбивает входные данные на несколько меньших наборов (их число равно numberSmaller). Эти меньшие наборы могут быть все одного размера или их размеры могут существенно различаться. Каждый из элементов исходного входного набора попадает по крайней мере в один из меньших наборов, однако один и тот же элемент может попасть в несколько наборов. Затем происходит рекурсивный вызов алгоритма DivideAndConquer на каждом из меньших входных множеств, а функция CombineSolutions сводит полученные результаты воедино.
|
|
Факториал натурального числа несложно вычислить в цикле, однако в нижеследующем примере нам понадобится рекурсивный вариант этого вычисления. Факториал числа N равен N, умноженному на факториал числа N — 1. Поэтому годится следующий алгоритм:
| Factorial(N) | |
| N | число, факториал которого нам нужен |
| Factorial | возвращает целое число |
|
| |
| if (N=l) then | |
| return 1 | |
| else | |
| smaller = N-l | |
| answer=Factorial(smaller) | |
| return (N*answer) | |
| end if | |
Шаги этого алгоритма просты и понятны, и мы можем сравнить их с приведенным выше стандартным алгоритмом. Хотя мы и упоминали ранее в этой главе, что операция умножения сложнее сложения и поэтому умножения надо подсчитывать отдельно, для упрощения примера мы не будем учитывать эту разницу.
При сопоставлении этих двух алгоритмов видно, что предельным размером данных в нашем случае служит 1, и при таких данных никаких арифметических операций не выполняется. Во всех остальных случаях мы переходим к залогу else. Первым шагом в общем алгоритме служит «разбиение ввода на более мелкие части»; в алгоритме вычисления факториала этому шагу соответствует вычисление переменной smaller, которое требует одного вычитания. Следующий шаг общего алгоритма представляет собой рекурсивный вызов процедур обработки более мелких данных; в алгоритме вычисления факториала — это один рекурсивный вызов, и размер задачи в нем на 1 меньше предыдущего. Последний шаг в общем алгоритме состоит в объединении решений; в алгоритме вычисления факториала это умножение в последнем операторе return.
Насколько эффективен рекурсивный алгоритм? Сможем ли мы подсчитать его эффективность, если будем знать, что алгоритм непосредственного вычисления квадратичен, разбиение входных данных логарифмично, а объединение решений линейно (все в зависимости от размеров входных данных), и что входные данные разбиваются на восемь частей, размер каждой из которых равен четверти исходного? Эту задачу не так-то легко решить, не очень-то понятно даже, как к ней приступать. Однако оказывается, что анализ алгоритмов вида «разделяй и властвуй» очень прост, если шаги Вашего алгоритма поставлены в соответствие шагам предложенного выше общего алгоритма этого вида: непосредственное вычисление, разбиение входа, некоторое количество рекурсивных вызовов и объединение полученных решений. Если известно, как эти шаги сочетаются друг с другом, и известна сложность каждого шага, то для определения сложности алгоритма
|
|
|
| |
| где | DAC — сложность алгоритма DivideAndConquer, |
| DIR — сложность алгоритма DirectSolution, | |
| DIV — сложность алгоритма Dividelnput, | |
| COM — сложность алгоритма CombineSolutions. | |
При наличии этой общей формулы ответ на вопрос, поставленный в начале предыдущего абзаца, оказывается совсем простым. Нам нужно лишь подставить в общую формулу известные сложности каждого куска. В результате получим

или даже проще, поскольку размеры всех меньших множеств одинаковы:
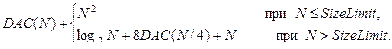
Равенства такого вида называются рекуррентными, поскольку значение функции выражено в терминах себя самого. Нам бы хотелось найти выражение для сложности, зависящее только от N, и не зависящее от других вызовов той же функции. Процесс исключения рекурсии из подобных равенств будет описан в следующем параграфе, где рекуррентные соотношения изучаются подробно.
Вернемся к примеру с факториалом. Мы сопоставили все этапы алгоритма вычисления факториала с общим алгоритмом DivideAndConquer. Воспользуемся теперь этим сопоставлением и определим значения, которые следует подставить в приведенную выше общую формулу. Непосредственные вычисления в функции Factorial не требуют действий, каждый из алгоритмов разбиения входных данных и объединения результатов требует по одному действию, и рекурсивный вызов решает задачу, размер данных которой на единицу меньше исходного. В результате мы получаем следующее рекуррентное соотношение на количество вычислений в функции Factorial:
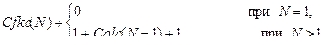
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!