Двумерная случайная величина  называется дискретной, если
называется дискретной, если  и
и  - дискретные величины.
- дискретные величины.
Пусть возможные значения  и
и  образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины
образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины  имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что
имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что 

Функция распределения и ее свойства.
Функция распределения F(х, у) имеет вид
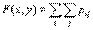
где двойная сумма распространена на те i и j, для которых xi<x и yj<y.
Двумерную случайную величину  так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины
так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины  , а первый столбец — возможные значения
, а первый столбец — возможные значения  . В остальных клетках таблицы указаны соответствующие вероятности, причем их сумма всегда равна единице. В качестве примера рассмотрим двумерную случайную величину, заданную следующей таблицей:
. В остальных клетках таблицы указаны соответствующие вероятности, причем их сумма всегда равна единице. В качестве примера рассмотрим двумерную случайную величину, заданную следующей таблицей:
 \ \ 
| -1
| 0
| 1
|
| 0,1
| p11=0,05
| p12=0,20
| p13=0,30
|
| 0,2
| p21=0,10
| p22=0,20
| p23=0,15
|
Сумма всех вероятностей

1) F (x, y) определена для всех (x, y) О R 2, так как вероятность P { X ≤ x, Y ≤ y } определена для всех x, y О R 1.
2) 0 ≤ F (x, y) ≤ 1 для всех x, y О R 1. По аксиоме A1 и свойству 5)P для любого события выполняется 0 ≤ P (A) ≤ 1, поэтому по определению F (x, y) О [0,1].
3) F (-∞, y) = F (x,-∞) = F (-∞,-∞) = 0 для всех x, y О R 1. Например, рассматривая
| Bn
| Δ =
| { ω: Y (ω) ≤ - n }, где n = 1, 2,...,
|
можно по аналогии с доказательством свойства 3)F(x) установить, что
| F (-∞, y) ≤
| l i m n →∞
| P(Bn) = P(Ж) = 0.
|
4) FY (y) = F (+∞, y), FX (x) = F (x,+∞) для всех x, y О R 1, где FX (y) и FY (x) - функции распределения СВ X и Y соответственно. Это свойство можно установить, следуя доказательству свойства 3)F(x), т.к. { ω: X (ω) ≤ +∞} = { ω: Y (ω) ≤ +∞} = Ω.
5) F (+∞,+∞) = 1. В силу свойства 4)F(x,y) имеем
| F (+∞,+∞) = F X (+∞)
| 3)F(x) =
| 1.
|
6) F (x, y) - монотонно неубывающая по каждому из аргументов. Т.к. для Δ x > 0 имеем
| F (x +Δ x, y)
| Δ =
| P{ X ≤ x +Δ x, Y ≤ y }
| A3 =
|
= P { X ≤ x, Y ≤ y } + P { x < X ≤ x + Δ x, Y ≤ y },
так как рассматриваемые события несовместны. По аксиоме A1 имеем F (x + Δ x, y) ≥ F (x, y). Монотонность F (x, y) по y доказывается аналогично.
7) Если F (x, y) непрерывна по x и y, то вероятность попадания СВ Z в прямоугольник D = { x 1 ≤ x ≤ x 2, y 1 ≤ y ≤ y 2} равна
| P(D)
| Δ =
| F (x 2, y 2) + F (x 1, y 1) - F (x 1, y 2) - F (x 2, y 1),
|
где F (xi, yj), (i, j = 1,2) - вероятности попадания СВ Z в квадранты Dij с соответствующими вершинами (xi, yj), i, j = 1,2
Матрица распределения.
Двумерная непрерывная случайная величина. ее геометр интерпретация.
Двумерная св (х;у) явл непрерывной, если ее ф-я распределения F(x;y) представляет собой дифференцируемую ф-ю по каждому из аргументов.
Плотность распределения двумерной случайной величины и ее свойства.
Неотрицательная функция f (x, y) называется плотностью распределения (плотностью вероятности) двумерной непрерывной СВ
если
| F (x, y) =
| x ∫ -∞
| (
| y ∫ -∞
| f (x, y) d y
| )
| d x = 1.
|
При этом двумерная СВ Z называется непрерывной.
1) f (x, y) ≥ 0 для всех x, y О R 1. Это вытекает из определения 1.
2)
| P(D) =
| x 2 ∫ x 1
| y 2 ∫ y 1
| f (x, y) d y d x, где
|
| D
| Δ =
| { x 1 ≤ x ≤ x 2, y 1 ≤ y ≤ y 2}.
|
По свойству 7)F(x,y) и определению 1 имеем
| P(D) = F (x 2, y 2) - F (x 2, y 1) - F (x 1, y 2) + F (x 1, y 1)
| Δ =
|
| Δ =
| x 2 ∫ -∞
| y 2 ∫ -∞
| f (x, y) d y d x -
| x 2 ∫ -∞
| y 1 ∫ -∞
| f (x, y) d y d x -
| x 1 ∫ -∞
| y 2 ∫ -∞
| f (x, y) d y d x +
|
| +
| x 1 ∫ -∞
| y 1 ∫ -∞
| f (x, y) d y d x =
| x 2 ∫ x 1
| y 2 ∫ y 1
| f (x, y) d y d x.
|
3)
| P(D) =
| ∫ ∫ D
| f (x, y) d x d y,
|
где D - произвольная область на плоскости R 2. Доказательство проведем для непрерывной f (x, y). Рассмотрим бесконечно малый прямоугольник
| Δ D
| Δ =
| { x ≤ X ≤ x + Δ x, y ≤ Y ≤ y + Δ y }.
|
Согласно свойству 2)f(x,y) можно записать
| P(Δ D) =
| x +Δ x ∫ x
| y +Δ y ∫ y
| f (x, y) d x d y =
| |
| по теореме о среднем значении
| |
| ≈ f (x, y) Δ y Δ x.
|
Таким образом, элемент вероятности f (x, y)d x d y с точностью до бесконечно малых высшего порядка равен вероятности попадания двумерной СВ Z = col(X, Y) в бесконечно малый прямоугольник, прилегающий к точке (x, y). Так как произвольную область D М R 2 можно представить с любой степенью точности в виде объединения конечного числа непересекающихся бесконечно малых прямоугольников Δ D, тоиз аксиомы A3 (см. замечание Л3.Р2.З2) следует формула для вероятности попадания СВ (X, Y) в D.
4)
| +∞ ∫ -∞
| +∞ ∫ -∞
| f (x, y) d y d x = 1,
|
поскольку
| +∞ ∫ -∞
| +∞ ∫ -∞
| f (x, y) d y d x
| Δ =
| F (+∞,+∞)
| 5)F(x,y) =
| 1.
|
5)
| F X (x) =
| x ∫ -∞
| +∞ ∫ -∞
| f (t, y) d y d t, FY (y) =
| y ∫ -∞
| +∞ ∫ -∞
| f (x, y) d x d y;,
|
где FX (x), FY (y) - функции распределения СВ X и Y. Например,
| FX (x)
| 4)F(x,y) =
| F (x,+∞)
| Δ =
| x ∫ -∞
| +∞ ∫ -∞
| f (x, y) d y d x.
|
Для FY (y) утверждение доказывается аналогично.
6)
| f X (x) =
| +∞ ∫ -∞
| f (x, y) d y, fY (y) =
| +∞ ∫ -∞
| f (x, y) d x.
|
Это вытекает из свойства 5) и определения Л4.Р3.О2.
7) Пусть СВ
где φ (x, y) - заданная скалярная функция аргументов x, y О R 1, такая что
| +∞ ∫ -∞
| +∞ ∫ -∞
| | φ (x, y)| f (x, y) d x d y < +∞.
|
Тогда можно показать, что
| M[ V ] =
| +∞ ∫ -∞
| +∞ ∫ -∞
| φ (x, y) f (x, y) d x d y.
|
8) Для независимости непрерывных СВ X и Y необходимо и достаточно, чтобы выполнялось равенство
f (x, y) = f X (x) fY (y)
во всех точках непрерывности этих функций. Действительно, по определению плотности
| y ∫ -∞
| x ∫ -∞
| f (x, y) d x d y = F (x, y) =
| ||
| в силу незави- симости
| ||
| = F X (x)F Y (y) =
|
| Л4.Р3.О2 =
| x ∫ -∞
| fX (x) d x
| y ∫ -∞
| fY (y) d y =
| x ∫ -∞
| y ∫ -∞
| fX (x)fY(y) d x d y.
|
Откуда следует свойство 8).
Замечание 2. Свойство 6)f(x,y) позволяет по плотности вероятности двумерной СВ Z найти плотность вероятности СВ X и Y.
9) Если непрерывные СВ X и Y независимы, то справедлива формула свертки плотностей, т.е. плотность распределения СВ
имеет вид
| fV (v) =
| +∞ ∫ -∞
| fX (x) fY (v-x) d x,
|
где fX (x), fY (y) -- плотность распределения СВ X и Y. Пусть
| D
| Δ =
| { x, y: x + y ≤ v }.
|
Тогда
| FV (v)
| Δ =
| P{ X + Y ≤ v }
| 2)f(x,y) =
| ∫ ∫ D
| f (x, y) d x d y
| 8)f(x,y) =
|
| =
| ∫ ∫ D
| fX (x), fY (y) d x d y =
| +∞ ∫ -∞
| fX (x) (
| v-x ∫ -∞
| fY (y) d y) d x =
| ||
| y
| Δ =
| t - x
| ||
| =
|
| =
| +∞ ∫ -∞
| fX (x) (
| v ∫ -∞
| fY (t-x) d t) d x =
| v ∫ -∞
| +∞ ∫ -∞
| fX (x) fY (t-x) d x d t.
|



 называется дискретной, если
называется дискретной, если  и
и  - дискретные величины.
- дискретные величины.  образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины
образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины  имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что
имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что 

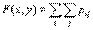
 так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины
так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины 



