Напомним сначала определение голоморфной функции.
Функция  называется голоморфной в точке
называется голоморфной в точке  , если она разложима в некоторой окрестности этой точки в степенной ряд по степеням
, если она разложима в некоторой окрестности этой точки в степенной ряд по степеням  :
:

 (1.1)
(1.1)
В этом случае говорят также, что  допускает в области
допускает в области  аналитическое представление в виде степенного ряда по степеням
аналитическое представление в виде степенного ряда по степеням  .
.
При этом на  и на представляющий её степенной ряд налагаются в указанной окрестности три условия:
и на представляющий её степенной ряд налагаются в указанной окрестности три условия:  определена, т.е. имеет конечное значение, ряд сходится и его сумма совпадает с
определена, т.е. имеет конечное значение, ряд сходится и его сумма совпадает с  .
.
Рассмотрим примеры голоморфных функций.
Пример 1.
Функции  ,
,  ,
,  голоморфны в точке
голоморфны в точке 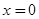 , т.к. известно:
, т.к. известно:
 ,
,  ,
, 
Причём ряды справа сходятся при  .
.
Пример 2.
Полином от 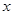 ,
,  ,
,  ,
,  - целые функции. В частности, при
- целые функции. В частности, при 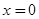 имеем известные разложения:
имеем известные разложения:

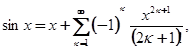
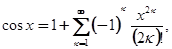
Причём ряды справа сходятся при всех 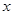 .
.
Пример 3.
Функция  является голоморфной в точке
является голоморфной в точке 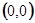 , т.к.
, т.к.

Причём ряд справа сходится в области  .
.
Важным частным случаем голоморфных функций являются функции, для которых представление (1.1) имеет место в окрестности любой точки  , а ряд сходится при всех значениях
, а ряд сходится при всех значениях 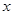 . Такие функции называются целыми. (Пример 2.)
. Такие функции называются целыми. (Пример 2.)
Данное выше определение голоморфности функции  распространяется на случай функции
распространяется на случай функции  , зависящей от n независимых переменных. Последняя называется голоморфной в точке
, зависящей от n независимых переменных. Последняя называется голоморфной в точке  , если
, если

Где ряд справа сходится в области 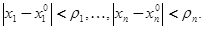 (пример 3.)
(пример 3.)
Вернёмся к функции  , зависящей от одной независимой переменной. Из теории степенных рядов известно, что если
, зависящей от одной независимой переменной. Из теории степенных рядов известно, что если  допускает разложение (1.1), то это разложение единственно; причём коэффициенты
допускает разложение (1.1), то это разложение единственно; причём коэффициенты  выражаются через значения
выражаются через значения  и её производных в точке
и её производных в точке  по известным формулам
по известным формулам


Поэтому разложение (1.1) можно переписать в виде
 (1.2)
(1.2)
Ряд справа называется рядом Тейлора для функции  в точке
в точке  .
.
Таким образом, всякий сходящийся степенной ряд Тейлора для своей суммы, и мы можем говорить, что функция  голоморфна в точке
голоморфна в точке  , если она допускает в окрестности этой точки разложение в ряд Тейлора. В частности, функция
, если она допускает в окрестности этой точки разложение в ряд Тейлора. В частности, функция  , для которой имеет место разложение
, для которой имеет место разложение

голоморфна в точке 0.
Из разложения (1.2) следует, что функция  , голоморфная в точке
, голоморфная в точке  , допускает следующее асимптотическое представление при
, допускает следующее асимптотическое представление при  :
:

Где 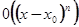 - бесконечно малая функция при
- бесконечно малая функция при  более высокого порядка малости, чем
более высокого порядка малости, чем  .
.
В частности, при  имеем асимптотическое представление
имеем асимптотическое представление

Отбросив все члены ряда Тейлора (1.2), кроме свободного и члена с первой степенью разности  , получаем линеаризацию функции
, получаем линеаризацию функции  в точке
в точке  :
:
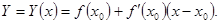 (1.3)
(1.3)
Геометрически (рис. 1.1) здесь речь идёт о замене отрезка графика функции  в достаточно малой окрестности точки
в достаточно малой окрестности точки  отрезком касательной (1.3) к нему в точке
отрезком касательной (1.3) к нему в точке 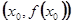 ,
,  Совершаемая при этом погрешность будет иметь порядок
Совершаемая при этом погрешность будет иметь порядок 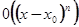 при
при  , т.е. является бесконечно малой функцией при
, т.е. является бесконечно малой функцией при  более высокого порядка малости, чем
более высокого порядка малости, чем  .
.


Рис. 1.1 Рис. 1.2
Обратимся теперь к задаче Коши.
Рассмотрим сначала задачу Коши для уравнения первого порядка в нормальной форме:
 (1.4)
(1.4)
Говорят, что задача (1.4) имеет решение
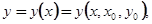 (1.5)
(1.5)
голоморфное в точке 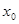 (т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке
(т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке 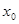 , т.е. представима в виде (1.1):
, т.е. представима в виде (1.1):

Или
 (1.6)
(1.6)
(здесь свободный член  есть начальное значение решения (1.5) при
есть начальное значение решения (1.5) при  ).
).
Линеаризация решения задачи Коши (1.4) в точке  имеет вид
имеет вид

Или

(т.к.  ).
).
Рассмотрим пример, в котором решение задачи Коши представимо в виде сходящегося степенного ряда.
Пример 4.
Найти голоморфное решение задачи Коши
 (1.7)
(1.7)
т.е. нужно найти функцию, которая удовлетворяла бы начальному условию 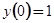 , дифференциальному уравнению
, дифференциальному уравнению  легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням
легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням 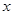 .
.
Интегрируя уравнение  , имеем
, имеем
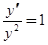

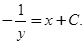
Удовлетворяя начальному условию 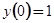 , находим, что
, находим, что  . Следовательно, искомым решением будет
. Следовательно, искомым решением будет
 (1.8)
(1.8)
Это решение представимо в окрестности начального значения  , т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом:
, т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом:
 (1.9)
(1.9)
Заметим, что решение (1.8) определено в более широком интервале  , так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал
, так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал 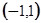 .
.
Линеаризацией в точке 0 будет

(см. рис. 1.2).
Для непосредственного нахождения голоморфного решения поставленной задачи Коши (1.7) можно использовать либо метод последовательного дифференцирования данного дифференциального уравнения, основанный на представлении решения в виде ряда Тейлора (ибо всякий сходящийся степенной ряд есть ряд Тейлора для его суммы), либо метод неопределенных коэффициентов. Рассмотрим оба эти метода.
Представляя искомое решение в виде ряда Тейлора по степеням  , имеем
, имеем
 (1.10)
(1.10)
Свободный член 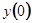 нам известен из начального условия
нам известен из начального условия  . Коэффициент при
. Коэффициент при  можно найти из дифференциального уравнения
можно найти из дифференциального уравнения  , положив в его обеих частях
, положив в его обеих частях  ; приняв во внимание начальное условие
; приняв во внимание начальное условие  , получим
, получим
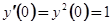 .
.
Далее, дифференцируя обе части уравнения  по
по  (при этом
(при этом  рассматривается как сложная функция от
рассматривается как сложная функция от  ), имеем:
), имеем:
 (1.11)
(1.11)
Полагая здесь  и заменяя y и
и заменяя y и  их значениями при
их значениями при  , получим
, получим

Дифференцируя (1.11) по  , найдем:
, найдем:
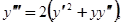
Откуда, полагая  , получим
, получим

Аналогично найдем,  Подставляя значение
Подставляя значение  и найденные значения производных от у в точке
и найденные значения производных от у в точке  в (1.10), получим снова разложение (1.9).
в (1.10), получим снова разложение (1.9).
В методе неопределенных коэффициентов голоморфное решение задачи Коши (1.7) ищется согласно (1.6) в виде
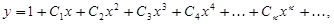 (1.12)
(1.12)
Где  - неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение
- неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение  и приравниванием коэффициентов при одинаковых степенях
и приравниванием коэффициентов при одинаковых степенях  в левой и правой частях полученного равенства (предполагая, что ряд (1.12) сходится, и, используя известную теорему о тождестве степенных рядов). Имеем
в левой и правой частях полученного равенства (предполагая, что ряд (1.12) сходится, и, используя известную теорему о тождестве степенных рядов). Имеем

Подставляя (1.12) в 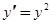 , получим
, получим

Выполняя, справа операцию возведения степенного ряда в квадрат, получим

Приравняем коэффициенты при одинаковых степенях  :
:

Определяя отсюда последовательно  найдем,
найдем,  Подставляя найденные значения
Подставляя найденные значения  в ряд (1.12), получим искомое решение в виде (1.9).
в ряд (1.12), получим искомое решение в виде (1.9).
Рассмотрим теперь задачу Коши для уравнения n-го порядка в нормальной форме
 (1.13)
(1.13)
Говорят, что задача (1.13) имеет решение
 (1.14)
(1.14)
Голоморфное в точке 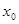 , если функция (1.14) голоморфна в точке
, если функция (1.14) голоморфна в точке  , т.е. представима в виде (1.1):
, т.е. представима в виде (1.1):

Или
 (1.15)
(1.15)
(Здесь  заданные начальные значения решения (1.13) при
заданные начальные значения решения (1.13) при  ). Коэффициенты
). Коэффициенты  так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.
так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.
Заметим, что формула (1.6) есть частный случай формулы (1.15) при n = 1. В этом последнем случае нам заранее известно лишь одно первое слагаемое 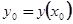 . Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений
. Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений
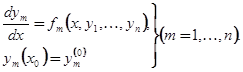 (1.16)
(1.16)
Решение этой задачи
 (1.17)
(1.17)
Называется голоморфным в точке  , если все функции (1.17) голоморфны в этой точке. Оно имеет вид
, если все функции (1.17) голоморфны в этой точке. Оно имеет вид
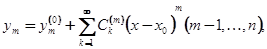
Где  - заданные числа (начальные значения искомых функций
- заданные числа (начальные значения искомых функций  ).
).



 называется голоморфной в точке
называется голоморфной в точке  , если она разложима в некоторой окрестности этой точки в степенной ряд по степеням
, если она разложима в некоторой окрестности этой точки в степенной ряд по степеням  :
:
 (1.1)
(1.1) допускает в области
допускает в области  .
. ,
,  ,
,  голоморфны в точке
голоморфны в точке 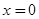 , т.к. известно:
, т.к. известно: ,
,  ,
, 
 .
.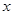 ,
,  ,
,  ,
,  - целые функции. В частности, при
- целые функции. В частности, при 
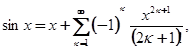
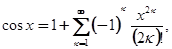
 является голоморфной в точке
является голоморфной в точке 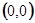 , т.к.
, т.к.
 .
. , а ряд сходится при всех значениях
, а ряд сходится при всех значениях  , зависящей от n независимых переменных. Последняя называется голоморфной в точке
, зависящей от n независимых переменных. Последняя называется голоморфной в точке  , если
, если
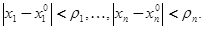 (пример 3.)
(пример 3.) выражаются через значения
выражаются через значения 

 (1.2)
(1.2)
 :
:
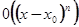 - бесконечно малая функция при
- бесконечно малая функция при  .
. имеем асимптотическое представление
имеем асимптотическое представление
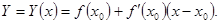 (1.3)
(1.3) в достаточно малой окрестности точки
в достаточно малой окрестности точки 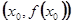 ,
,  Совершаемая при этом погрешность будет иметь порядок
Совершаемая при этом погрешность будет иметь порядок 

 (1.4)
(1.4)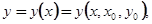 (1.5)
(1.5)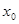 (т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке
(т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке 
 (1.6)
(1.6) есть начальное значение решения (1.5) при
есть начальное значение решения (1.5) при  ).
). имеет вид
имеет вид

 ).
). (1.7)
(1.7)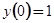 , дифференциальному уравнению
, дифференциальному уравнению  легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням
легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням 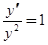

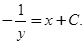
 . Следовательно, искомым решением будет
. Следовательно, искомым решением будет (1.8)
(1.8) , т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом:
, т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом: (1.9)
(1.9) , так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал
, так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал 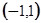 .
.
 , имеем
, имеем (1.10)
(1.10)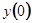 нам известен из начального условия
нам известен из начального условия  . Коэффициент при
. Коэффициент при  ; приняв во внимание начальное условие
; приняв во внимание начальное условие 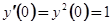 .
. (при этом
(при этом  рассматривается как сложная функция от
рассматривается как сложная функция от  (1.11)
(1.11) их значениями при
их значениями при 
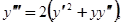

 Подставляя значение
Подставляя значение  и найденные значения производных от у в точке
и найденные значения производных от у в точке 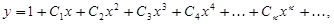 (1.12)
(1.12) - неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение
- неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение  и приравниванием коэффициентов при одинаковых степенях
и приравниванием коэффициентов при одинаковых степенях 
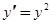 , получим
, получим


 найдем,
найдем,  Подставляя найденные значения
Подставляя найденные значения  (1.13)
(1.13) (1.14)
(1.14)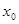 , если функция (1.14) голоморфна в точке
, если функция (1.14) голоморфна в точке  , т.е. представима в виде (1.1):
, т.е. представима в виде (1.1):
 (1.15)
(1.15) заданные начальные значения решения (1.13) при
заданные начальные значения решения (1.13) при  ). Коэффициенты
). Коэффициенты  так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.
так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.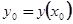 . Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений
. Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений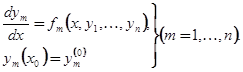 (1.16)
(1.16) (1.17)
(1.17) , если все функции (1.17) голоморфны в этой точке. Оно имеет вид
, если все функции (1.17) голоморфны в этой точке. Оно имеет вид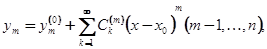
 - заданные числа (начальные значения искомых функций
- заданные числа (начальные значения искомых функций  ).
).


