Применение численных методов для вычисления кратных интегралов

 

Ограничимся рассмотрением двойных интегралов вида

,                                         (6.14)

где G – область интегрирования; - подынтегральная функция, например,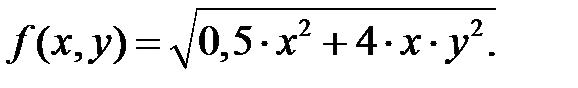

Одним из простейших методов вычисления интеграла (6.14) является метод ячеек [7]. Будет рассмотрен случай, когда область интегрирования G является прямоугольником:

           

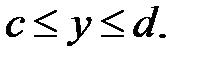
По теореме о среднем найдем среднее значение функции :

                       ,       (6.15)

где S – площадь области интегрирования G.

Будем считать, что среднее значение  приблизительно равно значению функции в центре прямоугольника, т.е.

,

где   - координаты центра прямоугольника. Теперь из (6.15) можно получить выражение для приближенного вычисления двойного интеграла:

            (6.16)

Точность этой формулы можно повысить, если разбить область G на прямоугольные ячейки Δ G_ij (см. рис. 6.3). В пределах ячейки Δ G_ij  

, (i = 1, 2, 3, …, m);

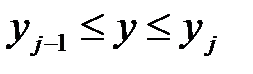, (j = 1, 2, 3, …, n).

Здесь m и n – количество элементарных отрезков соответственно на осях х и у (количество узловых точек соответственно равно m + 1и n + 1). Количество ячеек равно m ∙ n. Длины сторон ячеек (длины элементарных отрезков):

                                , . 

Рис. 6.3. Схема метода ячеек

 

Применяя к каждой ячейке Δ G_ij формулу (6.16), получим:

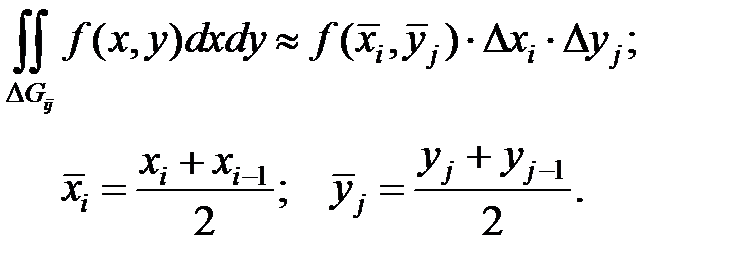                                                (6.17)

Суммируя эти выражения по всем ячейкам, находим значение двойного интеграла

                     .                 (6.18)

В правой части стоит интегральная сумма. Поэтому при неограниченном уменьшении периметров ячеек (или стягивании их в точки при   и 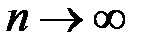) эта сумма стремится к точному значению интеграла для любой непрерывной функции .

Для повышения точности используют обычные методы сгущения узлов

сетки путем увеличения m и n. При этом по каждой переменной (х и у) шаги

уменьшают в одинаковое число раз, т.е. отношение m / n остается постоянным.

Другим довольно распространенным методом вычисления кратных интегралов является метод последовательного вычисления определенных интегралов [7]. Интеграл I для прямоугольной области можно записать в виде

                                                                 (6.19)

  Для вычисления обоих определенных интегралов могут быть использованы рассмотренные ранее численные методы. Например, метод трапеций.

Пример вычисления двойного интеграла методом ячеек

Вычислить интеграл

                          .                           (6.20)

Здесь подынтегральная функция  ; ; ; ; .

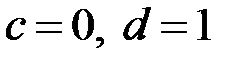Примем количество элементарных отрезков на осях х и у соответственно m = 4, n = 4(количество узловых точек m + 1 = 5 и   n + 1 = 5). Тогда размеры ячеек:   

            .

Количество ячеек m ∙ n = 4∙4= 16. Расчетная схема представлена на рис. 6.4. Внутри ячеек проставлены их порядковые номера. Координаты узловых точек: x ₀ = 1,0; x ₁ = 1,5;…; x ₄ = 3; y ₀ = 0; y ₁ = 0,25;…;    y ₄ = 1,0. 

Вычисление интеграла (6.20) выполняем непосредственно по формуле (6.18) с учетом того, что размеры всех ячеек одинаковы, т.е.  и

:

Рис. 6.4. Расчетная схема к вычислению интеграла (6.20)

 

Пример вычисления двойного интеграла методом последовательного вычисления определенных интегралов

Вычислим интеграл (6.20) с использованием формул (6.19). Количество элементарных отрезков и, следовательно, размеры ячеек ,  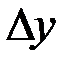и координаты узловых точек такие же, как и в примере, рассмотренном в разделе 6.6.

Для вычисления определенных интегралов, входящих в (6.19), будем использовать формулу трапеций (6.12). Запишем эту формулу применительно к вычислению значения  (второе выражение в (6.19)) при фиксированном значении х:

.  (6.21)

Формулу (6.21) последовательно применим для вычисления  при       х _i = 1,0; 1,5; 2,0; 2,5; 3,0:

; ; .

Здесь вычисления подынтегральной функции производились по формуле

. Например, при х = 1,5 и у = 0,25

.

  Формулу трапеций (6.12) применительно к вычислению двойного интеграла I  (первое выражение в (6.19)) запишем следующим образом:  

        (6.22)

Подставляя ранее вычисленные значения  в выражение (6.22), получим

.

При вычислении по формуле ячеек этого же интеграла в разделе 6.6 ранее получили I = 10,218. Таким образом, относительное отклонение составляет:

.

Отметим, что вычисление двойного интеграла методом последовательного вычисления определенных интегралов по сравнению с методом ячеек требует большего количества вычислений.