 22. Примеры применения к расчету электростатических полей: плоскости и шара.
22. Примеры применения к расчету электростатических полей: плоскости и шара.
 Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE. Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4). Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE. Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4). Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).
 где
где  - угол между силовой линией и нормалью
- угол между силовой линией и нормалью  к площадке dS;
к площадке dS;  - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен
- проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен
 Так как Так как  , то , то  где где  - проекция вектора - проекция вектора 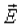 на нормаль и к поверхности dS. на нормаль и к поверхности dS.
| |
Теорема Остроградского-Гаусса: Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную e0.
Доказательство:
 Определим поток напряженности электростатического поля вакууме (e=1) через произвольную замкнутую сферическую поверхность радиусом R, окружающей один заряд +q, находящийся в ее центре
Определим поток напряженности электростатического поля вакууме (e=1) через произвольную замкнутую сферическую поверхность радиусом R, окружающей один заряд +q, находящийся в ее центре
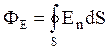 , где
, где  - есть интеграл по замкнутой поверхности сферы. Во всех точках сферы модуль вектора
- есть интеграл по замкнутой поверхности сферы. Во всех точках сферы модуль вектора  одинаков, а сам он направлен перпендикулярно поверхности. Следовательно
одинаков, а сам он направлен перпендикулярно поверхности. Следовательно  .
.
Площадь поверхности сферы равна  . Отсюда следует, что
. Отсюда следует, что
 .
.
Рассмотрим самый общий случай поверхности произвольной формы, охватывающей n зарядов.По принципу суперпозиции электростатических полей напряженность  , создаваемая зарядами q1,q2,...qn равна векторной сумме напряженностей, создаваемых каждым зарядом в отдельности:
, создаваемая зарядами q1,q2,...qn равна векторной сумме напряженностей, создаваемых каждым зарядом в отдельности:  . Проекция вектора
. Проекция вектора  - результирующей напряженности поля на направление нормали к площадке dS равна алгебраической сумме проекций всех векторов
- результирующей напряженности поля на направление нормали к площадке dS равна алгебраической сумме проекций всех векторов  на это направление:
на это направление:  , отсюда
, отсюда  .
.
Когда заряд 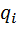 расположен внутри поверхности S, он дает вклад в поток, равный
расположен внутри поверхности S, он дает вклад в поток, равный  . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
. В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
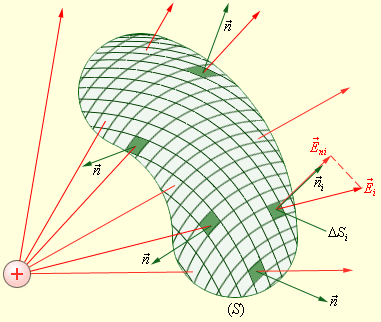 Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий

В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью  , различной в разных местах пространства. Тогда суммарный заряд объема V, охватываемого замкнутой поверхностью S равен
, различной в разных местах пространства. Тогда суммарный заряд объема V, охватываемого замкнутой поверхностью S равен  и теорему Гаусса следует записать в виде
и теорему Гаусса следует записать в виде  . Теорема Гаусса представляет значительный практический интерес: с ее помощью можно определить напряженности полей, создаваемых заряженными телами различной формы.
. Теорема Гаусса представляет значительный практический интерес: с ее помощью можно определить напряженности полей, создаваемых заряженными телами различной формы.
Физический смысл этого утверждения заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная деформация поверхности не изменит полного числа линий напряженности, выходящих наружу.
Если замкнутая поверхность произвольной формы охватывает заряд (рис. 125), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее. Нечетное число  пересечений при вычислении потока в конечном счете сводится к одному пересечению, таккак поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.
пересечений при вычислении потока в конечном счете сводится к одному пересечению, таккак поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.
Электростатическая теорема Гаусса. Она устанавливает математическую связь между потом вектора напряженности через замкнутую поверхность и зарядами, находящимися в объеме, ограниченном данной поверхностью. Предположим, что имеется некоторый объем V, ограниченный поверхностью S и точечный заряд Q внутри этого объема. Рассмотрим поток N напряженности 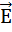 сквозь эту поверхность. Так как Q точечный заряд. То напряженность поля равна
сквозь эту поверхность. Так как Q точечный заряд. То напряженность поля равна  ; Bведем понятие телесного угла dΩ:
; Bведем понятие телесного угла dΩ:  ; (Количественной мерой телесного угла является отношение площади поверхности фрагмента сферы, вырезаемой конусом с вершиной в центре сферы. К квадрату радиуса этой сферы
; (Количественной мерой телесного угла является отношение площади поверхности фрагмента сферы, вырезаемой конусом с вершиной в центре сферы. К квадрату радиуса этой сферы  Таким образом,
Таким образом,  - телесный угол.) Полный телесный угол, под которым видна замкнутая поверхность из точек внутри объема, равен 4π, а поток
- телесный угол.) Полный телесный угол, под которым видна замкнутая поверхность из точек внутри объема, равен 4π, а поток  ;
;
Дифференциальная форма теоремы
Поток напряженности электрического поля через произвольную замкнутую поверхность определяется зарядом внутри этой поверхности.
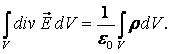 ,отсюда
,отсюда  .
.
**************(http://tsput.ru/res/fizika/1/KR_ELEC/l4.htm более-менее о дивергенции)****************
Применение теоремы Гаусса для расчета электрических полей.
 1.Поле равномерно заряженной плоскости.
1.Поле равномерно заряженной плоскости.
Электрическое поле, создаваемое бесконечно протяженной равномерно заряженной плоскостью, является однородным – в каждой точке пространства вне плоскости его напряженность всюду одинакова. Направлено это поле перпендикулярно к плоскости в обе стороны. Поэтому для потока вектора напряженности поля через произвольно выбранную цилиндрическую поверхность,  опирающуюся на элемент плоскости ΔS, можем написать:
опирающуюся на элемент плоскости ΔS, можем написать:


 - поверхностная плотность заряда. Размерность в СИ:
- поверхностная плотность заряда. Размерность в СИ:
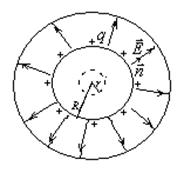 Поле равномерно заряженного шара.
Поле равномерно заряженного шара.
Металлический шар. При равновесии заряды равномерно распределяются по внешней поверхности заряженного шара. Поэтому при r < R (внутри шара) электрическое поле отсутствует:


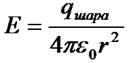
 Вне шара r > R электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Гаусса:
Вне шара r > R электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Гаусса:
Видим, что электрическое поле равномерно заряженного металлического шара не зависит от радиуса шара и совпадает с полем точечного заряда.



 22. Примеры применения к расчету электростатических полей: плоскости и шара.
22. Примеры применения к расчету электростатических полей: плоскости и шара. Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE. Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4). Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE. Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4). Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5). где
где  - угол между силовой линией и нормалью
- угол между силовой линией и нормалью  к площадке dS;
к площадке dS;  - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен
- проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен Так как
Так как  , то
, то  где
где  - проекция вектора
- проекция вектора 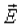 на нормаль и к поверхности dS.
на нормаль и к поверхности dS.
 Определим поток напряженности электростатического поля вакууме (e=1) через произвольную замкнутую сферическую поверхность радиусом R, окружающей один заряд +q, находящийся в ее центре
Определим поток напряженности электростатического поля вакууме (e=1) через произвольную замкнутую сферическую поверхность радиусом R, окружающей один заряд +q, находящийся в ее центре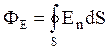 , где
, где  - есть интеграл по замкнутой поверхности сферы. Во всех точках сферы модуль вектора
- есть интеграл по замкнутой поверхности сферы. Во всех точках сферы модуль вектора  одинаков, а сам он направлен перпендикулярно поверхности. Следовательно
одинаков, а сам он направлен перпендикулярно поверхности. Следовательно  .
. . Отсюда следует, что
. Отсюда следует, что .
. . Проекция вектора
. Проекция вектора  на это направление:
на это направление:  , отсюда
, отсюда  .
.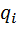 расположен внутри поверхности S, он дает вклад в поток, равный
расположен внутри поверхности S, он дает вклад в поток, равный  . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
. В случае расположения заряда снаружи поверхности его вклад в поток есть нуль. Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий
 , различной в разных местах пространства. Тогда суммарный заряд объема V, охватываемого замкнутой поверхностью S равен
, различной в разных местах пространства. Тогда суммарный заряд объема V, охватываемого замкнутой поверхностью S равен  и теорему Гаусса следует записать в виде
и теорему Гаусса следует записать в виде  . Теорема Гаусса представляет значительный практический интерес: с ее помощью можно определить напряженности полей, создаваемых заряженными телами различной формы.
. Теорема Гаусса представляет значительный практический интерес: с ее помощью можно определить напряженности полей, создаваемых заряженными телами различной формы. пересечений при вычислении потока в конечном счете сводится к одному пересечению, таккак поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.
пересечений при вычислении потока в конечном счете сводится к одному пересечению, таккак поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.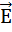 сквозь эту поверхность. Так как Q точечный заряд. То напряженность поля равна
сквозь эту поверхность. Так как Q точечный заряд. То напряженность поля равна  ; Bведем понятие телесного угла dΩ:
; Bведем понятие телесного угла dΩ:  ; (Количественной мерой телесного угла является отношение площади поверхности фрагмента сферы, вырезаемой конусом с вершиной в центре сферы. К квадрату радиуса этой сферы
; (Количественной мерой телесного угла является отношение площади поверхности фрагмента сферы, вырезаемой конусом с вершиной в центре сферы. К квадрату радиуса этой сферы  Таким образом,
Таким образом,  - телесный угол.) Полный телесный угол, под которым видна замкнутая поверхность из точек внутри объема, равен 4π, а поток
- телесный угол.) Полный телесный угол, под которым видна замкнутая поверхность из точек внутри объема, равен 4π, а поток  ;
;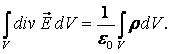 ,отсюда
,отсюда  .
. 1.Поле равномерно заряженной плоскости.
1.Поле равномерно заряженной плоскости. опирающуюся на элемент плоскости ΔS, можем написать:
опирающуюся на элемент плоскости ΔS, можем написать:

 - поверхностная плотность заряда. Размерность в СИ:
- поверхностная плотность заряда. Размерность в СИ: Поле равномерно заряженного шара.
Поле равномерно заряженного шара.

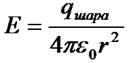
 Вне шара r > R электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Гаусса:
Вне шара r > R электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Гаусса:

