ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Ю.И. РАЗИНОВ, П.П. СУХАНОВ
ГИДРАВЛИКА
И ГИДРАВЛИЧЕСКИЕ МАШИНЫ
Учебное пособие
КАЗАНЬ
КГТУ
2010
УДК 62-82(075)
ББК 30.123
Разинов Ю.И, Суханов П.П.
Гидравлика и гидравлические машины: учебное пособие /
Ю.И. Разинов, П.П. Суханов. – Казань: Изд-во Казан. гос. технол.
ун-та, 2010. - 168с.
Пособие соответствует государственным образовательным стандартам дисциплин «Гидравлика», «Гидравлика и гидравлические машины», «Механика жидкости», «Прикладная гидромеханика» и предназначено для студентов механических специальностей, в учебных планах которых предусмотрены соответствующие курсы.
Особое внимание в пособии уделяется темам, связанным с гидравлическими расчетами при проектировании химико-технологических процессов, машин и аппаратов.
Подготовлено на кафедре ПАХТ КГТУ.
Печатается по решению редакционно-издательского совета
Казанского государственного технологического университета.
Рецензенты: д-р техн. наук, проф. КГЭУ А.Я. Мутрисков
д-р техн. наук, проф. КГСА А.И. Рудаков
ISBN © Разинов Ю.И., 2010
© Казанский государственный
технологический университет, 2010
ОГЛАВЛЕНИЕ
Предисловие 7
Часть I. Гидравлика 8
Глава 1. Основные понятия гидравлики 8
1.1. Введение. Предмет гидравлики. Модели жидкой среды 8
1.2. Физические свойства жидкостей 11
1.3. Поток жидкости и его параметры.
Струйная модель потока 17
1.4. Виды и режимы движения жидкостей 20
1.5. Силы и напряжения, действующие в жидкостях 23
Глава 2. Основные законы гидравлики 24
1.6. Уравнения расхода для элементарной струйки и потока
жидкости 24
1.7. Дифференциальные уравнения неразрывности. Уравнение
неразрывности для потока несжимаемой жидкости 26
1.8. Дифференциальные уравнения движения вязкой
несжимаемой и идеальной жидкостей 30
1.9. Уравнение Бернулли для установившегося движения
элементарной струйки идеальной жидкости 34
1.10. Примеры использования уравнения Бернулли в технике 37
1.11. Гидростатика. Дифференциальные уравнения равновесия
и абсолютного покоя 39
1.12. Основное уравнение гидростатики и его следствия.
Примеры использования закона Паскаля в технике 41
1.13. Сила давления жидкости на поверхности 44
1.14. Относительный покой жидкости
во вращающемся резервуаре 47
1.15. Уравнение Бернулли для потока вязкой жидкости 50
1.16. Потерянный напор. Виды потерь напора 53
1.17. Основы теории гидродинамического подобия 53
1.18. Потери напора по длине потока.
Формула Дарси-Вейсбаха 59
1.19. Потери напора по длине ламинарного потока 61
1.20. Потери напора по длине турбулентного потока.
График Никурадзе 65
1.21. Местные потери напора. Теорема Борда 71
1.22. Неустановившееся движение несжимаемой жидкости
в трубопроводах. Инерционный напор 76
1.23. Гидравлический удар 78
1.24. Взаимодействие потока жидкости с твердыми телами 82
Глава 3. Гидравлический расчет трубопроводов 86
1.25. Общие сведения 86
1.26. Расчет простого трубопровода.
Характеристика трубопроводной сети 88
1.27. Расчет сифонного трубопровода 89
1.28. Расчет сложных трубопроводов 90
1.29. Основы расчета газопроводов 93
1.30. Понятие о технико-экономическом расчете
трубопровода 95
ЧАСТЬ I. ГИДРАВЛИКА
ГЛАВА 1. Основные понятия гидравлики
Введение. Предмет гидравлики.
Модели жидкой среды
При решении различных технических проблем часто приходится встречаться с процессами движения различных жидкостей и их силовым воздействием на твердые тела. Исследование указанных процессов привело к созданию науки, которая называется “Механика жидкого тела“ или “Гидромеханика”.
Гидромеханика изучает общие закономерности покоя, равновесия и движения жидкостей, их силовое воздействие на твердые тела, а также способы применения указанных закономерностей к решению различных инженерных задач.
Предметом изучения в гидромеханике является в основном поведение так называемых капельных жидкостей (жидкостей, способных образовывать капли) – например, воды, бензина, глицерина и т.д. Капельные жидкости по своему молекулярному строению занимают промежуточное положение между твердыми телами и газами. По плотности они близки к твердым телам (молекулы находятся примерно на таких же расстояниях, что и в твердом состоянии, поэтому силы сцепления достаточно высоки). В то же время капельные жидкости обладают большой подвижностью (текучестью), характерной для газов. Математическое описание подобных промежуточных состояний, когда проявляются и, соответственно, требуют учета свойства обоих исходных состояний, представляет значительную сложность, что и было отмечено учеными довольно давно. В частности, знаменитый математик и астроном Галилей несколько веков назад сказал, что гораздо легче изучить поведение бесконечно удаленных от Земли небесных тел, чем движение воды в ручейке, протекающем у наших ног. Это объясняется тем, что в механике твердого тела мы имеем систему жестко связанных между собой твердых частиц, жидкость же является совокупностью множества подвижных частиц, перемещающихся относительно друг друга. Прошли века и жизнь подтвердила справедливость высказывания Галилея. До сего времени не удалось разрешить в общем виде дифференциальных уравнений движения реальной жидкости. Поэтому исторически изучение гидромеханики проходило по двум направлениям:
1. ТЕОРЕТИЧЕСКОЕ, основоположниками которого являлись И.Ньютон, Л.Эйлер, Д.Бернулли и другие знаменитые математики и механики. Решения, которые получает теоретическая гидромеханика, являются более общими и более строгими, однако весьма сложны, не учитывают ряд факторов, не слишком удобны и поэтому малопригодны для инженерных расчетов.
2. ТЕХНИЧЕСКОЕ (экспериментальное), которое развивалось, в основном, французскими инженерами. В технической гидромеханике используются упрощающие допущения, экспериментальные данные (эмпирические уравнения), а решения имеют приближенный характер.
В первой трети двадцатого века наметилась тенденция к сближению указанных направлений - используются теоретические методы исследования, результаты которых уточняются введением экспериментальных поправок. Такой подход использует гидравлика - прикладная наука, синтезирующая теоретический и экспериментальный методы исследования поведения жидкостей. Название образовано из греческих слов ”хюдор“(вода) и “аулос”(трубы) и относится к тому периоду человеческой истории, когда преимущественно изучалось течение воды по трубам.
Таким образом, гидравлика зародилась в глубокой древности. Исходно ее элементарные закономерности использовались для решения жизненно-важных вопросов - орошения полей, строительства мельниц и плотин, водоснабжения городов, кораблестроения и т.д. Наиболее известными учеными древности и эпохи Возрождения в области гидравлики являются Архимед (исследовал законы гидростатики и плавания тел, создал ряд уникальных механизмов и гидромеханических устройств) и Леонардо да Винчи (изучал работу гидравлического пресса, истечение жидкостей из отверстий, интерференцию волн, изобрел центробежный насос, парашют и т.д.). Теоретические основы современной гидравлики заложены в XVII и XVIII веках трудами уже упомянутых Ньютона, Эйлера, Бернулли. Российские ученые–гидравлики внесли свою лепту в развитие гидравлики в XIX и XX веках: Жуковский создал теорию гидравлического удара, Петров обосновал гидродинамическую теорию смазки, а Громека создал теорию винтовых потоков.
Роль гидравлики в современной технике весьма высока. Гидравлика дает методы расчета и проектирования различных гидротехнических сооружений (плотин, каналов, трубопроводов), гидравлических машин (насосов, турбин, гидропередач).
Особенно велика роль гидравлики в машиностроении. Гидросистемы, состоящие из насосов, трубопроводов и различных гидроагрегатов, широко используются в системах топливоподачи, смазки, охлаждения современных машин, станков, автомобилей, самолетов и т.д. Все более широкое применение находят гидроприводы и гидроавтоматика в машиностроении, системах комплексной механизации и автоматизации различных производств.
Под жидкостью в гидравлике понимают физическое тело, состоящее из частиц, обладающих большой подвижностью. Жидкости способны к необратимой деформации сдвига под влиянием весьма малых касательных напряжений. Таким свойством обладают не только капельные жидкости, но и газы, поэтому термин “жидкость“ распространяют и на них. Законы движения капельных жидкостей при определенных условиях можно использовать и для газов.
Предложены упрощенные представления о жидкостях – модели жидких тел. Л. Эйлер предложил использовать модель сплошной жидкой среды. Это позволило считать параметры потока жидкости (скорость, давление, плотность) непрерывными функциями координат и времени, и в связи с этим использовать аппараты дифференциального и интегрального исчисления. Используется также модель идеальной жидкости – воображаемой жидкой среды, не обладающей вязкостью и сжимаемостью. Применяется и струйная модель потока (направленно движущейся), согласно которой поток мыслится как совокупность множества очень тонких (элементарных) струек. Особенности индивидуального поведения и взаимодействия этих струек между собой и(или) окружающей средой определяют закономерности макроскопического поведения потоков в различных условиях.
Струйная модель потока
Поток – это направленное движение жидкости, ограниченное поверхностями раздела фаз; чаще всего – это твердые поверхности (стенки трубопроводов или аппаратов), но могут быть и другие среды (газы или жидкости), не смешивающиеся с данной движущейся жидкостью. Для сравнения различных потоков используют геометрические и гидравлические параметры.
Геометрические параметры потока. Живое сечение – это поверхность в границах потока, нормальная во всех точках к векторам скоростей струек, из которых состоит поток. Если поток однонаправленный – живое сечение является плоским. Для цилиндрической трубы, полностью заполненной движущейся жидкостью, живое сечение – круг. Площадь живого сечения обозначим S.
Смоченный периметр – это часть контура живого сечения, по которой поток соприкасается с твердыми стенками. Длину смоченного периметра обозначим П. Тогда (рис.3):
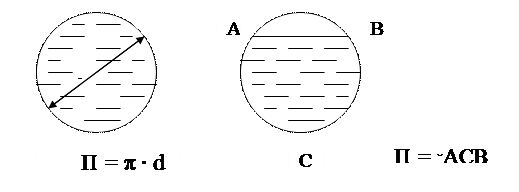
А б
Рис. 3. Иллюстрация длины контурасмоченного периметра (П) живого сечения круглой формы в случае полного (а) и частичного (б) смачивания твердой поверхности границы потока
Таким образом, в случае частичного заполнения жидкостью сечения твердого трубопровода (рис. 3б) смоченный периметр определяется по незамкнутому контуру (дуге) АСВ и не включает в себя отрезок АВ, соответствующий границе раздела между жидкой и газовой фазами.
Гидравлический радиус – r г =  – это отношение площади S живого сечения к длине смоченного периметра П. Ему соответствует d э - эквивалентный диаметр, причем для цилиндрического трубопровода, полностью заполненного жидкостью и имеющего диаметр d, выполняется соотношение: d э = 4 r г = 4·(π d ²)/(4·π d) = d, т.е. в цилиндрической трубе гидравлический и геометрический диаметры совпадают. Поэтому понятие d э целесообразно вводить для потока, имеющего сложную форму живого сечения. Для такого потока d э – диаметр условного (воображаемого) цилиндрического потока, у которого отношение
– это отношение площади S живого сечения к длине смоченного периметра П. Ему соответствует d э - эквивалентный диаметр, причем для цилиндрического трубопровода, полностью заполненного жидкостью и имеющего диаметр d, выполняется соотношение: d э = 4 r г = 4·(π d ²)/(4·π d) = d, т.е. в цилиндрической трубе гидравлический и геометрический диаметры совпадают. Поэтому понятие d э целесообразно вводить для потока, имеющего сложную форму живого сечения. Для такого потока d э – диаметр условного (воображаемого) цилиндрического потока, у которого отношение  такое же, как и у реального потока.
такое же, как и у реального потока.
Гидравлические параметры потока. Расход – это количество жидкости, протекающей через данное живое сечение в единицу времени. В зависимости от того, в каких единицах измеряется количество жидкости, различают:
Q – объемный расход; М – массовый расход; G – весовой расход.
Они связаны между собой соотношением: М = ρ·Q; G = ρ g Q.
Давление в движущейся жидкости (гидродинамическое давление) различно в направлениях x,y и z из-за наличия касательных сил внутреннего трения. В общем случае р = р (x, y, z, t).
Скорость движения жидкости (или ее элементов) представляет собой вектор, компоненты которого также изменяются как в пространстве, так и во времени, т.е. υ i = υ i (x, y, z, t), где i = x, y, z. В дальнейшем векторная природа скорости будет учитываться только там, где это безусловно необходимо, поскольку при элементарном рассмотрении гидромеханических явлений можно обойтись одной ее координатой (например, параллельной направлению потока).
Как уже отмечалось, скорости в фиксированных точках движущейся жидкости называются местными (например, скорости движения в различных точках живого сечения потока). В целом поток можно представить как совокупность множества очень тонких параллельных струек, каждая из которых движется со своей скоростью (струйная модель потока).
Струйная модель потока. Чтобы уточнить понятие “элементарная струйка” жидкости, используем ряд вспомогательных понятий.
Линия тока – это кривая, проведенная внутри движущейся жидкости так, что вектор скорости в каждой точке направлен по касательной к этой кривой.
Трубка тока – это совокупность линий тока, проведенных через каждую точку замкнутого элементарного контура.
Элементарная струйка – это часть потока, заключенная внутри трубки тока (содержимое трубки тока).
а б
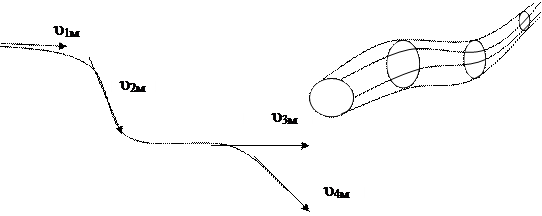

Рис. 4. Элементы струйной модели потока:
а – линия тока, б - трубка тока
Свойства элементарной струйки:
1. Скорости жидкости в любой точке живого сечения можно считать одинаковыми (поскольку сечение является бесконечно малым).
2. Стенки элементарной струйки непроницаемы для жидкости (жидкость может двигаться лишь вдоль струйки).
Местные скорости могут быть усреднены во времени:
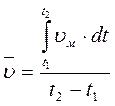
где υм - текущее значение м естной скорости.
Местные скорости усредняются также и в пространстве (например, по живому сечению потока):
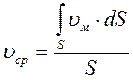
Понятием “средняя скорость потока” широко пользуются в гидравлике, поэтому скорость υ по умолчанию (если не оговорено иное) считается “средней” и индекс “ср” обычно опускается.
И потока жидкости
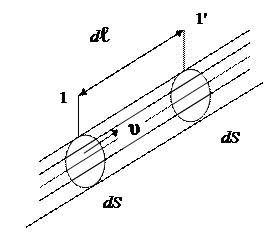 Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.
Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.
Определим расход жидкости
Рис. 9. Иллюстрация через сечение dS:
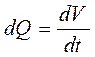 к выводу уравнения
к выводу уравнения
объемного расхода ,
где dV - объем жидкости, заключенный между положением 1 и 1'.
Поскольку объем цилиндрического тела dV = dS · d ℓ, то
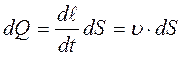
Таким образом получаем уравнение объемного расходадля элементарной струйки:
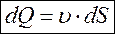
Согласно струйной модели, поток жидкости представляет собой совокупность множества элементарных струек, поэтому:
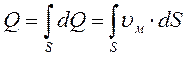
где υм - местные скорости в сечении S (скорости различных элементарных струек). Интеграл можно взять, если известен закон распределения местных скоростей по сечению потока. Этот закон теоретически определен только для ламинарного потока, поэтому в гидравлике при выводе общего выражения для Q используется упрощение – вводится средняя скорость по сечению потока, с помощью которой определяется уравнение расхода для потока жидкости:
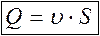
где 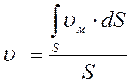 (см. раздел 1.23)
(см. раздел 1.23)
Таким образом, υ - это условная, постоянная для данного сечения (средняя) скорость потока, которая обеспечивает такой же расход, как и при реальном распределении скоростей. В гидравлических расчетах используют именно среднюю скорость, поскольку определение местных скоростей весьма затруднительно. Кроме того, для элементарной струйки можно считать υ м = υ ср ≡ υ.
1.7. Дифференциальные уравнения неразрывности. Уравнение неразрывности для потока
Несжимаемой жидкости
Уравнения неразрывности для элементарной струйки и одномерного потока жидкости.

Рис. 10. Иллюстрация к выводу уравнения неразрывности
для элементарной струйки
Выберем в элементарной струйке два сечения 1 и 2 (живые сечения dS 1 и dS 2) на конечном расстоянии друг от друга (рис. 10). Согласно струйной модели потока, параметры движущейся жидкости (скорость, плотность) изменяются только по одной координате (вдоль пути струйки, и тогда υ м = υ). Через время dt сечение 1 смещается в положение 1', а сечение 2 - в положение 2'. Тогда масса жидкости, вошедшей в объем между сечениями 1 и 2:
dm1 = dM1 · dt = ρ1 υ 1 · dS1· dt
а масса жидкости, вышедшей из объема между сечениями 1 и 2:
dm 2 = dM 2 · dt = ρ 2 υ 2 ∙ dS 2 · dt
Согласно закону сохранения массы, а также благодаря одному из свойств элементарной струйки (непроницаемости ее стенок) можно констатировать, что dm 1 = dm 2, откуда
ρ 1 υ 1 · dS 1 ∙ dt = ρ 2 υ 2 · dS 2 ∙ dt
После сокращения получаем уравнение неразрывности для элементарной струйки сжимаемой жидкости:
ρ 1 υ 1 · dS 1 = ρ 2 υ 2 · dS 2
Для несжимаемой жидкости ρ 1 = ρ 2 = const, поэтому
υ 1 · dS 1 = υ 2 · dS 2 (*)
Чтобы перейти к потоку жидкости, нужно проинтегрировать каждое из сечений по всем элементарным струйкам, проходящим через них. При этом необходимо помнить, что у каждой из струек скорость своя и единственная, хотя в рамках потока она одна из многих – т.е. местная (υ м). С учетом этого интегрируем левую часть уравнения (*) по площади S 1, а правую часть - по площади S 2:
∫ υ 1м · dS 1 = ∫ υ 2м · dS 2
s1 s2
И после перехода от местных к средним скоростям по потоку (т.е. по всем элементарным струйкам), которые представляют собой константы для каждого из сечений 1 и 2, и интегрирования по сечениям dS 1 и · dS 2, получаем уравнение неразрывности для одномерного потока несжимаемой жидкости:
υ 1 · S 1 = υ 2 · S 2
Его следствие: 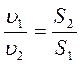 , т.е.
, т.е.
средние скорости обратно пропорциональны площадям живых сечений потока. Индекс “ср”, как уже указывалось, в практических приложениях обычно опускают.
Физический смысл уравнения неразрывности состоит в том, что он является проявлением закона сохранения массы для потока жидкости.
Дифференциальные уравнения неразрывности для трехмерного течения жидкости. Для трехмерного течения и неустановившегося движения справедливо:
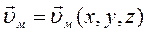 , ρ = ρ(х,y,z,t)
, ρ = ρ(х,y,z,t)
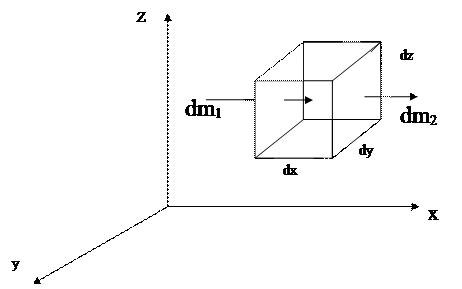
Рис. 1 1. Иллюстрация к выводу уравнения неразрывности
для трехмерного течения жидкости
Выделим внутри потока жидкости неподвижный элементарный параллелепипед (рис. 11) с ребрами dx, dy, dz. Согласно и аналогично полученному нами уравнению расхода для элементарной струйки, массовый расход жидкости, входящей в левую грань элементарного параллелепипеда (в направлении оси x) составит:
dM 1 = ρ υ м x · dS = ρ υ м x ∙ dydz
Тогда масса жидкости, вошедшей в левую грань за время dt:
dm 1 = dM 1 · dt = ρ υ м x ∙ dx dy dz dt
На противоположной (правой) грани параллелепипеда скорость жидкости и ее плотность могут измениться, поэтому массу жидкости, вышедшей из правой грани, следует записать:
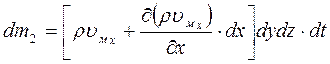
Отсюда изменение массы в объеме параллелепипеда в направлении оси x:
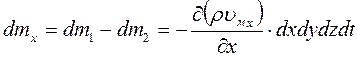
По аналогии изменение массы в направлениях осей y и z:
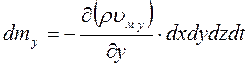
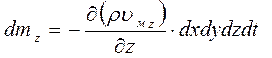
Полное изменение массы в объеме параллелепипеда:
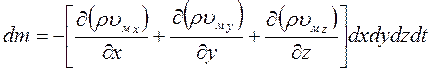
C другой стороны, исходя из определения плотности как предела отношения массы к объему, изменение массы dm в объеме параллелепипеда может быть представлено как конечное изменение плотности жидкости за время ее пребывания в фиксированном бесконечно малом объеме:
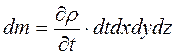
Приравняем два варианта выражения для dm:
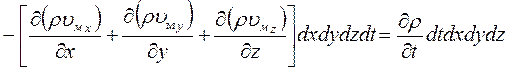
После сокращения получаем дифференциальное уравнение неразрывности для неустановившегося движения сжимаемой жидкости:
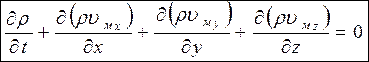
Для установившегося движения ∂ρ/∂ t = 0 (плотность не изменяется во времени). Для несжимаемой жидкости плотность не изменяется не только во времени, но и в пространстве (ρ = const), поэтому уравнение упрощается и переходит в дифференциальное уравнение неразрывности для установившегося движения несжимаемой (капельной) жидкости:
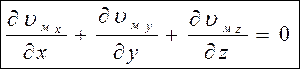
Дифференциальные уравнения движения
вязкой несжимаемой и идеальной жидкостей
Рассмотрим трехмерное неустановившееся ламинарное течение вязкой жидкости. В этом случае все гидравлические параметры потока и касательные напряжения сдвига являются функциями трех пространственных координат и времени.
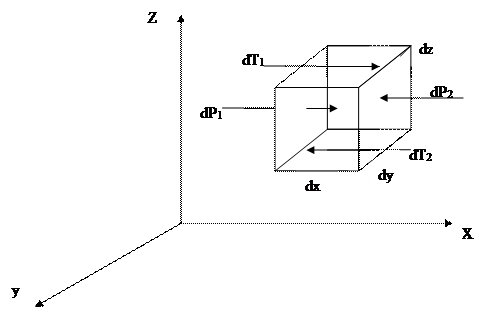
Рис. 12. Динамика движения жидкости в потоке
Выделим в массе движущейся жидкости неподвижный элементарный параллелепипед с длиной ребер dx, dy, dz (рис. 12). Масса жидкости в объеме параллелепипеда:
dm = ρ · dV = ρ ∙ dx dy dz
Используем основной принцип динамики: сумма сил, действующих на тело (в данном случае – на жидкость в объеме параллелепипеда) равна произведению его массы на ускорение, полученное в результате действия данных сил:
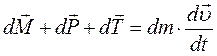
Рассмотрим данное уравнение в скалярной форме (в проекции на одну из осей координат – например, ось x):
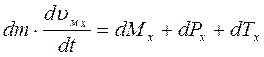
где dMx -проекция массовых сил на ось х;
dPx – проекция сил давления на ось х;
dTx – проекция сил вязкого трения на ось х.
При этом массовые силы пропорциональны массе жидкости и по закону Ньютона:
dMx = dm · X
где Х – проекция ускорения массовых сил на ось х. Соответственно:
dMy = dm · Y; dMz = dm · Z.
Силы давления действуют по всем граням параллелепипеда, однако эти силы (кроме dP1 и dP2) перпендикулярны оси х, поэтому их проекции на ось х равны 0 (мы их не изобразили на схеме, чтобы не перегружать чертеж). Но сила давления, действующая на левую грань, равна
dP 1 = p · dS = p · dy dz
При переходе жидкости из левой грани в правую (в направлении оси х) давление изменяется, что в дифференциальной форме может быть записано как p + (∂ p /∂ x) · dx, из чего следует:
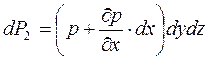
Это позволяет найти равнодействующую сил давления в направлении оси х:
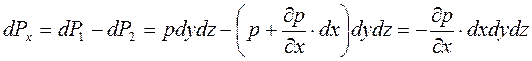
В общем случае при движении вязкой жидкости по всем граням параллелепипеда возникают касательные силы (силы вязкого трения).
В направлении оси х действуют только dT1 и dT2 (остальные силы дадут проекции, равные 0, поэтому на схеме не изображены):
dT 1 = τ · dx dy; 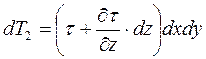
Записанные выражения справедливы лишь для одномерного течения (мы полагали, что υ м х изменяется только по координате z).
Для дальнейшего их обсуждения обратимся к закону вязкого трения:
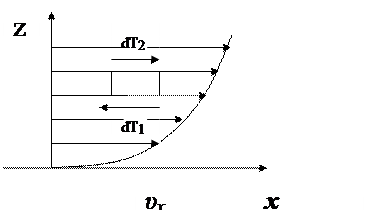

Рис. 1 3. Схема послойного течения жидкости
Исходя из модели послойного (ламинарного) течения жидкости (рис. 13) закон вязкого трения можно записать в виде:
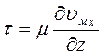
Для поля скоростей, изображенного на схеме, сила трения dT2 направлена слева направо, поскольку слой жидкости, движущейся над параллелепипедом, стремится сдвинуть параллелепипед в направлении скорости υx.
Сила трения dT1 направлена в обратную сторону, так как слой жидкости, движущейся под параллелепипедом, имеет меньшую скорость и подтормаживает жидкость на нижней грани параллелепипеда. При этом равнодействующая сил вязкого трения в направлении оси х равна:
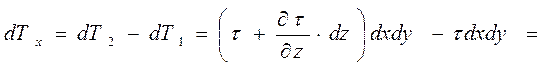
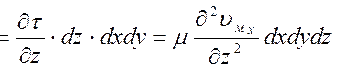
Имея в виду, что в общем случае течение может быть трехмерным, получаем:
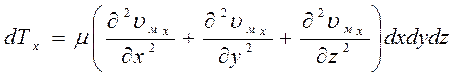
Подставляем значения проекций сил в основное уравнение:
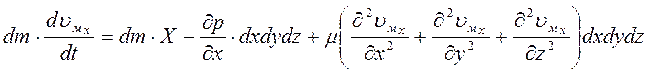
Поскольку dm = ρ ∙ dx dy dz, то в случае несжимаемой жидкости, когда ρ = const, получаем возможность делить на
ρ ∙ dx dy dz. Отсюда (c учетом того, что μ/ρ = ν):
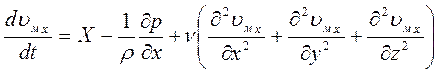
Здесь выражение в скобках – оператор Лапласа, поэтому более компактно дифференциальные уравнения движения вязкой несжимаемой жидкости в проекциях на все три координатные оси можно записать в виде:
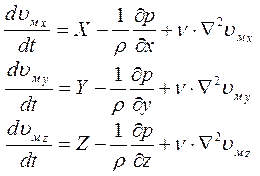
Полученная система уравнений (ее называют также уравнениями Навье - Стокса) не имеет общего решения, однако может быть использована:
1. Для решения наиболее простых гидродинамических задач;
2. Для постановки и решения более сложных задач численными методами с помощью современных компьютеров;
3. Для получения критериев гидродинамического подобия.
Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера). В идеальной жидкости вязкость отсутствует (ν = 0), поэтому последний член правой части уравнений Навье – Стокса становится равным 0. В результате уравнения упрощаются (переходят в систему уравнений движения Эйлера):
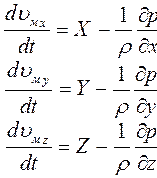
Интегрирование данной системы дифференциальных уравнений приводит к получению важнейшего уравнения гидродинамики – уравнения Бернулли.
Примеры использования уравнения Бернулли
в технике
1. Струйный насос
Рассмотрим принципиальную схему струйного насоса (рис. 14). Здесь во входное сопло подается поток вспомогательной жидкости (обычно вода или водяной пар).
Уравнение Бернулли для этой жидкости:
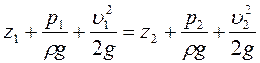
причем z1 = z2 (т.к. жидкость обычно перемещается горизонтально).

Рис. 14. Принципиальная схема действия струйного насоса:
1.Входное коническое
сопло
2.Камера смешения
3.Нагнетательный
патрубок
4.Всасывающий
трубопровод
5.Питательный
резервуар
Таким образом, по ходу движения скорость жидкости увеличивается (сечение уменьшается) и увеличивается скоростной напор (кинетическая составляющая полного напора). Поскольку суммарный напор должен быть постоянным, пьезометрический напор (потенциальная составляющая полного напора) будет уменьшаться по ходу движения жидкости по соплу. При этом геометрия сопла должна быть рассчитана таким образом, чтобы давление в сечении 2 – 2 становилось меньше атмосферного. Давление на свободной поверхности в питательном резервуаре равно атмосферному, поэтому транспортируемая жидкость под действием образовавшегося перепада давлений будет подниматься по всасывающему трубопроводу и подсасываться в камеру смешения. Здесь она смешивается со вспомогательной жидкостью и они общим потоком двигаются в нагнетательный патрубок.
2. Дроссельные расходомеры
Примером дроссельного расходомера является расходометр Вентури (рис. 15). Прежде всего с помощью расходомера осуществляется плавное сужение потока. При этом скорость в сечении 2 – 2 увеличивается, а давление уменьшается. В результате здесь, как и для струйного насоса, выполняется:
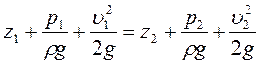
Поскольку z1 = z2 (поток горизонтальный), то
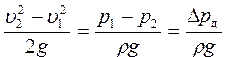
причем падение давления ∆pд может быть измерено с помощью дифференциального манометра D.

Рис. 15. Принципиальная схема дроссельного расходомера Вентури
Если к полученному соотношению добавить уравнение неразрывности потока: υ1S1 = υ2S2., то получается система двух уравнений с двумя неизвестными (υ1 и υ2), из которой можно определить υ1 и найти расход: Q = υ1· S1.
Для более точного определения расхода следует использовать уравнение Бернулли, записанное для реальной (вязкой) жидкости.
В технике
После интегрирования дифференциального уравнения абсолютного покоя получаем:
p + ρgz = const
Используем полученное уравнение для определения давления в точке А, находящейся внутри покоящейся жидкости (рис. 16). Для этого рассмотрим два сечения покоящейся жидкости – одно на уровне точки А, второе – на уровне свободной поверхности жидкости в резервуаре. Пусть давление на свободную поверхность равно ро, а Н – глубина погружения точки А. Тогда:
рА + ρg zA = p 2 + ρg z 2
Поскольку zA = 0, z2 = H, то после соответствующих преобразований получаем основное уравнение гидростатики:
 рА = р0 + ρ g H
рА = р0 + ρ g H
где z – высота расположения сечения относительно какой-то горизонтальной поверхности (плоскости сравнения 0 - 0). Второе слагаемое правой части




 – это отношение площади S живого сечения к длине смоченного периметра П. Ему соответствует d э - эквивалентный диаметр, причем для цилиндрического трубопровода, полностью заполненного жидкостью и имеющего диаметр d, выполняется соотношение: d э = 4 r г = 4·(π d ²)/(4·π d) = d, т.е. в цилиндрической трубе гидравлический и геометрический диаметры совпадают. Поэтому понятие d э целесообразно вводить для потока, имеющего сложную форму живого сечения. Для такого потока d э – диаметр условного (воображаемого) цилиндрического потока, у которого отношение
– это отношение площади S живого сечения к длине смоченного периметра П. Ему соответствует d э - эквивалентный диаметр, причем для цилиндрического трубопровода, полностью заполненного жидкостью и имеющего диаметр d, выполняется соотношение: d э = 4 r г = 4·(π d ²)/(4·π d) = d, т.е. в цилиндрической трубе гидравлический и геометрический диаметры совпадают. Поэтому понятие d э целесообразно вводить для потока, имеющего сложную форму живого сечения. Для такого потока d э – диаметр условного (воображаемого) цилиндрического потока, у которого отношение  такое же, как и у реального потока.
такое же, как и у реального потока.

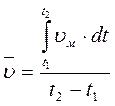
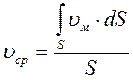
 Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.
Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.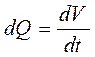 к выводу уравнения
к выводу уравнения 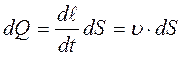
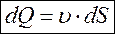
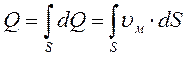
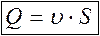
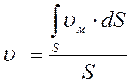 (см. раздел 1.23)
(см. раздел 1.23) 
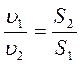 , т.е.
, т.е.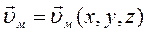 , ρ = ρ(х,y,z,t)
, ρ = ρ(х,y,z,t)
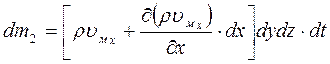
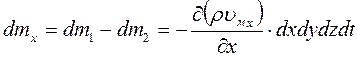
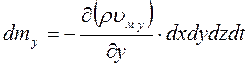
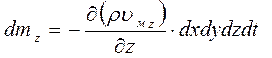
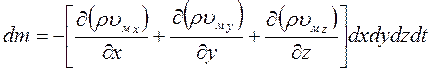
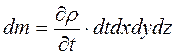
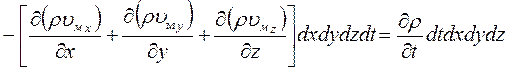
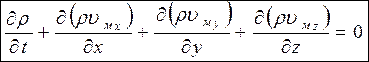
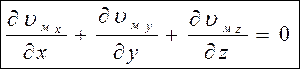

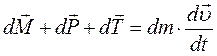
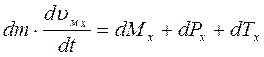
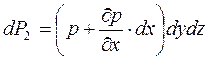
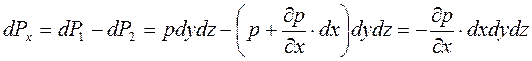
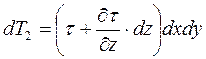


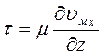
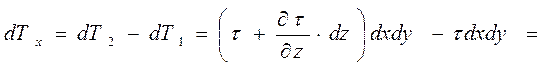
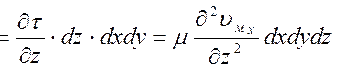
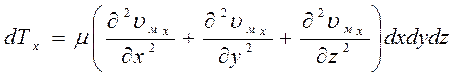
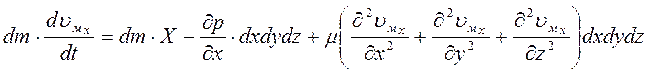
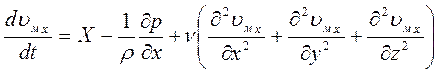
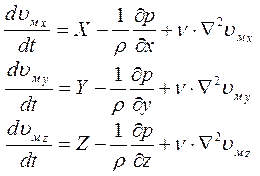
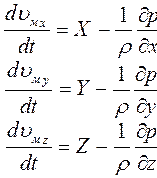
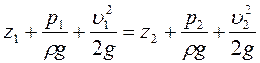

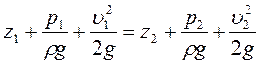
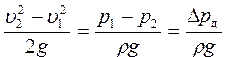

 рА = р0 + ρ g H
рА = р0 + ρ g H

