Определение ускорений точек плоской фигуры

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

 

№2

 

Поступательное и вращательное движение твердого тела. Примеры

1. Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы. 2. Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости - перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения.
3. Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени, w = df/dt и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом. 4. Линейная скорость v произвольной точки М вращающегося тела определяется как векторное произведение по формуле Эйлера v = [wr] где r - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение v линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения: v = wr sina = wR где a - угол между векторами w и r. 5. Периодом обращения Т тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол f = 2p. 6. Угловым ускорением называется вектор e, равный первой производной от вектора угловой скорости по времени: e = dw/dt Угловое ускорение характеризует быстроту изменения во времени вектора угловой скорости тела. При вращении вокруг неподвижной оси направление вектора w сохраняется и e = dw/dt = d2f/dt2 причем вектор e совпадает но направлению с w в случае ускоренного вращения (e > 0) и противоположен ему по направлению в случае замедленного вращения (e < 0) Линейное ускорение произвольной точки М (r) вращающегося тела равно a = dv/dt = d/dt | wr | = | er | + | w | wr ||
Катающийся цилиндр остановлен силой 1 кг. Масса цилиндра 2 кг, путь торможения 0,5 м. Вычислить скорость цилиндра до торможения.

Решение:

Полная энергия катающегося тела равна сумме кинетических энергий поступательного и вращательного движений: W = , (19)

где - I - момент инерции тела относительно оси, проходящей через центр

тяжести параллельно образующей;

- угловая скорость тела.

Момент инерции сплошного цилиндра относительно его оси равен

I = , где r - радиус цилиндра.

Линейная скорость точек поверхности качения , то есть .

Подставим I и в (19): W = .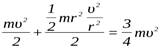

Кинетическая энергия цилиндра погашена работой силы торможения, то есть

F × S = .

Искомая скорость 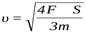. Вычисляем: м/с; м/с.

 

№3 Определение скоростей при плоскопараллельном движении твердого тела.

Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 1). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.

 

Рис.1 Рис.2

 

Рассмотрим сечение S тела какой-нибудь плоскости О xy, параллельной плоскости П (рис.2). При плоскопараллельном движе­нии все точки тела, лежащие на прямой ММ ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно.

Отсюда заключаем, что для изучения движения всего тела дос­таточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.

Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис.1). В свою очередь положение отрезка АВ можно определить, зная координаты x _A и y _A точки А и угол , который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.

При движении фигуры величины x _A и y _A и будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости

Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твер­дого тела.

Первые два из уравнений движения определяют то движение, которое фигура совершала бы при =const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движе­ние, которое фигура совершала бы при и , т.е. когда полюс А неподвижен; это будет вращение фи­гуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из по­ступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.

Основными кинематическими характеристиками рассматривае­мого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса , а также угловая скорость и угловое ускорение враща­тельного движения вокруг полюса.

 

№4 Определение ускорений при плоскопараллельном движении твердого тела.

Рис.14 Рис.15

 

Наконец, когда точка М движется криволинейно и ее траекто­рия известна, то 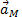можно заменить суммой .

 

№5 Сложное движение точки и твердого тела. Относительное, переносное и абсолютное движение. Примеры.

Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.

Такое движение точки называется сложным или составным.

Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.

Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).

Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.

Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.

Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.

 

№6 Теоремы о сложении скоростей при сложном движении. Примеры.

Теорема сложения ускорений (теорема Кориолиса)

Абсолютное 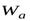ускорение точки в её сложном движении складывается геометрически из переносного , относительного и кориолисова (поворотного) ускорений.

Доказательство

Дифференцируя по времени равенство (1.3.10) и группируя подобные члены получим следующее выражение абсолютного ускорения точки:

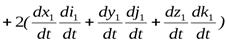. (1.3.12)

Обозначим

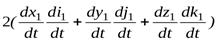. (1.3.13)

Тогда в силу выражений (1.3.8), (1.3.7) и (1.3.3) равенство (1.3.12) запишется:

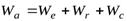, (1.3.14)

что требовалось доказать.

- поворотное или кориолисово ускорение.

 

№7 Теоремы о сложении ускорений при сложном движении. Примеры.

Ускорение Кориолиса

При поступательном движении подвижной системы отсчёта орты постоянны по направлению. Следовательно, кориолисово ускорение обращается в нуль. В этом случае теорема сложения ускорений выражается равенством: .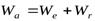

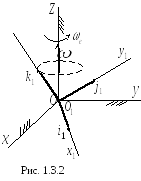
Рассмотрим другой частный случай: подвижная система отсчёта вращается вокруг неподвижной оси Oz (рис. 1.3.2). В этом случае концы ортов можно рассматривать как точки твёрдого тела, вращающегося вокруг неподвижной оси, скорости которых определяются формулой (1.2.20), то есть , , .

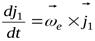Подставляя эти выражения в (1.3.13) и принимая во внимание (1.3.2), получим 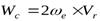. (1.3.15)

По определению векторного произведения двух векторов и вектор кориолисова ускорения перпендикулярен вектору и и направлен в ту сторону, откуда поворот вектора к вектору на меньший угол виден против хода часовой стрелки (рис. 1.3.3).

Направление можно определять по правилу Жуковского: направление совпадает с направлением проекции вектора на плоскость, перпендику-лярную вектору , повёрнутой в этой плоскости на угол 90⁰ в сторону вращения подвижной системы отсчёта.

Модуль кориолисова ускорения равен:

W_c = 2ω_e V_r sin (), (1.3.16)

г де ()- меньшийугол между векторами и .

В общем случае, когда относительное и переносное движения точки М совершаются по криволинейным траекториям, составляющие и теоремы Кориолиса записываются в проекциях на естественные оси:

. (1.3.17)

В задачах, как правило, материальная точка или твёрдое тело, принимаемое за материальную точку, движется относительно твёрдого тела, вращающегося вокруг неподвижной оси.

 

№8 Предмет статики. Аксиомы статики.

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Исследованием движения нетвердых тел – упругих, пластичных, жидких, газообразных, занимаются другие науки (сопротивление мате­риалов, теория упругости, гидродинамика и т.д.).

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

Аксиомы статики.

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F ₁ = F ₂) и направлены вдоль одной прямой в противоположные стороны

Аксиома1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Аксиома4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но проти­воположное по направлению противодействие.

Закон о равенстве действия и противодей­ствия является одним из основных законов ме­ханики

Аксиома 5 (принцип отвердевания). Равновесие изме­няемого (деформируемого) тела, находящегося под действием дан­ной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сва­ренными друг с другом и т. д.

Аксиома 6 (аксиома связей).Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.

Аксиома 1 Аксиома 2 Аксиома3 Аксиома 4

№9 Типы связей и их реакции. Момент силы относительно центра и оси. Пара сил. Вектор момент пары сил. Условия равновесия систем пар сил. Примеры.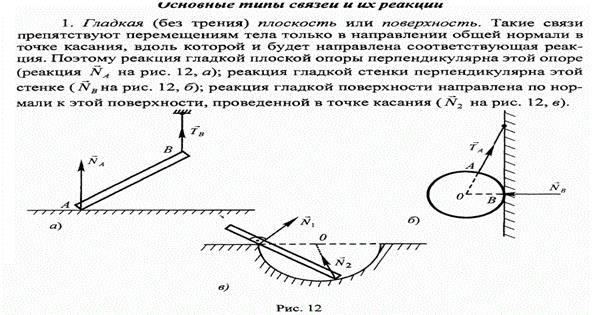

 

 

№10 Главный вектор и главный момент системы сил. Примеры

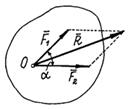
Рассмотрим плоскую систему сил (F ₁, F ₂,..., F _n),действующих на твердое тело в координатной плоскости Oxy.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F ₁ + F ₂ +... + F _n = F _i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L _O, равный сумме векторных моментов этих сил относительно точки О:

L _O = M _O(F ₁) + M _O(F ₂) +... + M _O(F _n) = M _O(F _i).

Вектор R не зависит от выбора центра О, а вектор L _O при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом L_O плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментовэтих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

К вершинам квадрата со стороной a = 0.5(м) приложены силы: F₁ = 4(Н); F₂ = F₃ = 8(Н); F₄ = 12(Н). Определить главный вектор этой системы сил и ее алгебраический главный момент относительно центра квадрата О.

Решение. Введем координатную систему Oxy, оси которой параллельны сторонам квадрата (в такой системе координат расчеты проводятся наиболее простым образом).

Силы F ₂, F ₃ образуют пару сил с моментом M₂₃ = -F₂·a=-4(Н·м) и их можно не учитывать при вычислении проекций главного вектора R:

R_х = F_1x + F_4x = -F₁ + F₄= -4 + 12 = 8(Н);

R_y = F_1y + F_4y = 0.

Вычисление алгебраического главного момента L_O проведем с использованием плеч сил F ₁ и F ₄, равных половине длины стороны квадрата (a/2):

L_O = F₁·a/2 - F₄·a/2 + M₂₃ = 1 - 4 + 3 = 0.

Таким образом, для заданной системы сил ее главный вектор равен по модулю R = 8(Н) и направлен вдоль оси Ox, а ее алгебраический главный момент L_O = 0.

Замечание. В случае, когда L_O = 0, главный вектор R является равнодействующей силой заданной системы сил.

 

№11 Произвольная пространственная система сил. Условия равновесия различных систем сил. Примеры.

Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).

Отсюда вытекает условие равновесия произвольной пространственной системы сил.

В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю

R = 0, M_О = 0.

В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю

ΣF_kx = 0, ΣF_ky = 0, ΣF_kz = 0,

M_x(F_k) = 0, M_y(F_k) = 0, M_z(F_k) = 0.

Условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей).

Чтобы задача была статически определимой, число неизвестных должно быть не более шести.

В частности, для системы параллельных сил условиями равновесия являются следующие равенства

Σ F_kx = 0, M_x(F_k) = 0, M_y(F_k) = 0.

 

№12 Равновесие системы соединенных тел. Примеры.

Статический расчет системы тел сводится к рассмотрению условий равновесия конструкций, состоящих из не жестко соединенных между собой тел. Связи между частями конструкции называются внутренними, скрепляющие конструкцию с другими телами, - внешними.

Системы тел, для которых число неизвестных реакций связей равно числу уравнений равновесия, называются статически определимыми. Если число неизвестныхреакций связейбольше числа уравнений равновесия (на одно, два и т.д.), то системы тел называются статически неопределимыми (соответственно один, два и т.д. раза). Такие задачи невозможно решить методами статики.

При решении задач на равновесие системы тел обычно конструкцию расчленяют на отдельные тела и составляют уравнения равновесия для каждого из тел в отдельности. При этом проверяют, не превышает ли число неизвестных реакций связей число уравнений равновесия, которые можно составить для данной конструкции

Пример. Для определения внутренних и внешних реакций связей трех шарнирной аркирасчленим конструкцию по соединительному шарниру С на две части и рассмотрим равновесие каждой из частей в отдельности. Внешние реакции шарниров А и В разложим на составляющие . Реакцию со стороны части СВ на АВ разложим на составляющие , а реакцию со стороны АС на ВС на составляющие . Так как по третьему закону Ньютона (аксиома 4, §1) , то неизвестных реакций связей в уравнения равновесия войдет шесть.

При действии на трех шарнирную арку заданной произвольной плоской системы сил для каждой части можно записать по три уравнения равновесия:

для АС для СВ

 

 

Следовательно, система тел, образующих арку, статически определима.

 

№13 Теорема Вариньона о моменте равнодействующей. Центр параллельных сил и центр тяжести тела. Координаты центра тяжести объема, площади и линии

Центр параллельных сил в пространстве. Центр тяжести. Свойства параллельных сил. Определение центра тяжести плоской фигуры, объема, линии

Центром тяжести твердого тела называется центр параллельных сил тяжести частиц, слагающих тело. Иными словами, центр тяжести – это такая точка приложения равнодействующей сил тяжести частиц тела, которая остаётся неизменной при любых поворотах тела.

Таким образом, для определения положения центра тяжести можно использовать формулы для координат центра параллельных сил.

Тело состоит из n элементарных объемов. Найдем равновесие такой системы сил, приложенных в некоторой точке C.

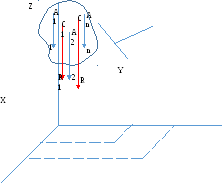Обозначим силы веса отдельных частиц тела , координаты его центра тяжести , координаты любой частицы твердого тела и , а вес будет равен

 

Тогда формулы для определения координат центра тяжести принимают вид:

; ;

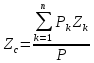
Определим положение центра тяжести однородных тел. Точка С – центр сил в пространстве с координатами

Свойства параллельных сил и равнодействующей:

1. Если силы повернуть в любом направлении на любой угол, то равнодействующая повернется на тот же угол и будет проходить через тоску С.

2. Если предположить, что P₁ и P₂ вес элементарных объемов, то равнодействующая будет являться весом, а точка С будет центром масс.

Координаты можно найти по теореме Вариньона:

1. Если в качестве P₁ и P_n представить элементарно малую фигуру, то

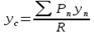
; ; - статический момент площади фигуры

1. Если в качестве P₁ и P_n представить элементарно малый объем, то

; ;

1. Если в качестве P₁ и P_n представить элементарно малую длину, то

; ;

 

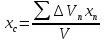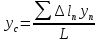№14 Равновесие при наличии сил трения. Законы Амонтона-Кулона. Момент сопротивления качению. Решение задач с учетом сил трения. Примеры.

При скольжении тела по шероховатой поверхности возникает сила реакции, которая имеет две составляющие – нормальную и силу трения скольжения (рисунок 2.1). Сила трения скольжения, приложенная к одному из трущихся тел, направлена противоположно его скорости относительно второго тела.

В результате экспериментальных исследований были установлены законы Амонтона-Кулона:

1. сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия (0 ≤ F_тр ≤ F_тр^max);

2. максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей;

F_тр^max = fN,                                                                              

где f – коэффициент трения скольжения, который является безразмерной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления.

Экспериментально установлено, что f < f_сц.

Рассмотрим твердое тело на шероховатой поверхности (рисунок 2.2), находящееся под действием активных сил в предельном состоянии равновесия, т.е. когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции.

В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол (R^max). Этот наибольший угол между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции и направлением нормальной реакции, называется углом трения φ:

tgφ = F_тр^max/N = fN/N = f.

Рисунок 2.2 Рисунок 2.3

Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях (рисунок 2.2).

При равновесии тела на шероховатой поверхности под действием силы P (рисунок 2.3) можно составить два уравнения равновесия:

ΣF_kx = 0; Psinα — F_тр = 0;

ΣF_ky = 0; -Pcosα + N = 0.

Следовательно,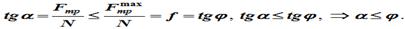

Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину.

Никакая сила, лежащая внутри конуса трения, не может вывести тело из состояния равновесия.

№15 Законы Ньютона. Первая задача динамики. Примеры.

Первый закон Ньютона утверждает, что

существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на него внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. На рис. 1 показано равномерное движение тела по льду при ничтожно малом коэффициенте трения между ним и поверхностью льда.

С высокой степенью точности инерциальной системой считается система отсчета, связанная с Солнцем (гелиоцентрическая). Если рассматриваемое время движения невелико, то инерциальной можно считать систему отсчета, связанную с Землей (геоцентрическая).

Второй закон Ньютона - основной закон динамики. Его можно сформулировать двумя способами:

1 ^-ая формулировка -
ускорение, приобретаемое телом в инерциальной системе отсчета прямо пропорционально действующей на него силе и обратно пропорциональна его массе a = F /m,
где F - равнодействующая всех сил, действующих на тело
F = S F _i.

2 ^-ая формулировка -
импульс силы равен изменению импульса тела
F ·Dt = m· V - m· V ₀

Третий закон Ньютона утверждает, что

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

 

№2

 

Поступательное и вращательное движение твердого тела. Примеры

1. Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы. 2. Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости - перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения.
3. Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени, w = df/dt и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом. 4. Линейная скорость v произвольной точки М вращающегося тела определяется как векторное произведение по формуле Эйлера v = [wr] где r - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение v линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения: v = wr sina = wR где a - угол между векторами w и r. 5. Периодом обращения Т тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол f = 2p. 6. Угловым ускорением называется вектор e, равный первой производной от вектора угловой скорости по времени: e = dw/dt Угловое ускорение характе