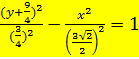Определение. Корнем  – ой степени из комплексного числа
– ой степени из комплексного числа 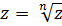 называется комплексное число
называется комплексное число  , такое, что
, такое, что  .
.
Пусть  ,
,
 .
.
Тогда  .
.
Отсюда  ,
,
 , где
, где  .
.
или  ,
,  , где
, где  .
.
т.е.  , где
, где  . (при прочих
. (при прочих  получим одно уже из выписанных значений корня).
получим одно уже из выписанных значений корня).
Из полученной формулы ясно, что  имеет
имеет  различных значений, модули которых равны, а аргументы отличаются на углы, кратнее
различных значений, модули которых равны, а аргументы отличаются на углы, кратнее  . Следовательно, соответствующие точки располагаются на окружности с центром в начале координат и радиусом
. Следовательно, соответствующие точки располагаются на окружности с центром в начале координат и радиусом  (рис.14).
(рис.14).

Пусть  и
и  целые положительные числа. Тогда
целые положительные числа. Тогда
 .
.
Теперь можно вычислить  , если
, если
 ,
,
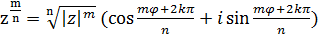 ,
,
 .
.
Примеры:
1) Найти все значения 
Решение:  ,
,
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
, 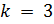 .
.
Все значения  лежат на окружности радиуса
лежат на окружности радиуса  на одинаковом угловом расстоянии
на одинаковом угловом расстоянии  друг от друга (рис. 15).
друг от друга (рис. 15).

2) Найти все значения  .
.
Решение:  ,
,
 ,
,  ;
;
 ,
,  ;
;
 ;
;
 ,
,  ;
;
 ,
, 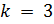 ;
;
 ,
,  .
.
(рис. 16)
Показательная форма записи комплексного числа
Наряду с уже введенными алгебраической и тригонометрической формами записи комплексного числа используется еще и, так называемая, показательная форма записи, которая получается из тригонометрической формы.
 .
.
Заменой выражения  с помощью формулы Эйлера
с помощью формулы Эйлера
 ,
,
которую примем без доказательства. Тогда комплексное число можно представить в виде  , где
, где  – модуль комплексного числа
– модуль комплексного числа  ,
,  – его аргумент.
– его аргумент.
Такая форма записи комплексного числа называется показательной формой записи.
Зная, как производятся действия над комплексными числами, записанными в тригонометрической форме, легко показать, что
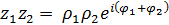 ,
,

 ,
,
 ,
,
 ,
,  .
.
Пример. Найти все значения  и записать результат в тригонометрической и показательной формах.
и записать результат в тригонометрической и показательной формах.
Решение: Запишем  в тригонометрической форме, для чего определим его модуль и аргумент
в тригонометрической форме, для чего определим его модуль и аргумент
 ,
,

Итак, 
Найдем теперь
 ,
,  .
.
В нашем случае
 ,
,  .
.
Поэтому  ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
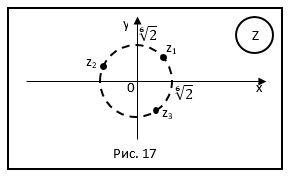
Приведя аргумент  к главному значению, получим
к главному значению, получим

(рис. 17)
Задачи для самостоятельного решения
Задача № 11. Следующие комплексные числа представить в тригонометрической и показательной формах
а)  б)
б)  в)
в)  ,
,
г)  , д)
, д)  , е)
, е) 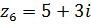 .
.
Задача № 12. Вычислить
а)  , б)
, б)  .
.
Задача № 13. Найти все значения корня
а)  , б)
, б)  , в)
, в)  , д)
, д)  .
.
Результат записать в алгебраической, тригонометрической и показательной формах.
В задачах №14-15 найти множество точек на плоскости комплексного переменного  , которые определяются заданными условиями.
, которые определяются заданными условиями.
Задача № 14.  .
.
Задача № 15.  (
( – действительное,
– действительное,  ).
).
В задачах № 16-19 указать какие линии определяются указанными уравнениями.
Задача № 16.  .
.
Задача № 17.  .
.
Задача № 18.  .
.
Задача № 19. 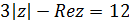 .
.
Нарисовать эти линии.
Ответы к задачам, предложенным для самостоятельного решения.
№ 1. Действительного решения нет.
№ 3.  ,
,  .
.
№ 6. Внутренность гиперболы  .
.
№ 7. Внутренность окружности  .
.
№ 8. Область, заключенная между окружностями
 и
и  .
.
№ 9. Гипербола  .
.
№ 10. Окружность  .
.
№ 12. а)  ; б)
; б)  .
.
№ 13.
а)  ;
;
б)  ;
;
в)  ,
,  ;
;
г)  .
.
№ 14. Часть плоскости, расположенная ниже прямой  .
.
№ 15. Внутренность единичной окружности.
№ 16. Эллипс  .
.
№ 17. Луч на оси  от
от  до
до  .
.
№ 18 Гипербола 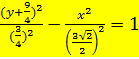
№ 19 Эллипс 



 – ой степени из комплексного числа
– ой степени из комплексного числа 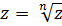 называется комплексное число
называется комплексное число  , такое, что
, такое, что  .
. ,
, .
. .
. ,
, , где
, где  .
. ,
,  , где
, где  , где
, где  . (при прочих
. (при прочих  получим одно уже из выписанных значений корня).
получим одно уже из выписанных значений корня). имеет
имеет  . Следовательно, соответствующие точки располагаются на окружности с центром в начале координат и радиусом
. Следовательно, соответствующие точки располагаются на окружности с центром в начале координат и радиусом  (рис.14).
(рис.14).
 и
и  .
. , если
, если ,
,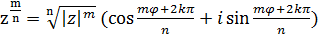 ,
, .
.
 ,
, ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
, 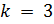 .
. лежат на окружности радиуса
лежат на окружности радиуса  на одинаковом угловом расстоянии
на одинаковом угловом расстоянии  друг от друга (рис. 15).
друг от друга (рис. 15).
 .
. ,
, ,
,  ;
; ,
,  ;
; ,
,  ,
,  ,
,  .
. .
. с помощью формулы Эйлера
с помощью формулы Эйлера ,
, , где
, где  – модуль комплексного числа
– модуль комплексного числа  – его аргумент.
– его аргумент.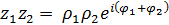 ,
,
 ,
, ,
, ,
,  и записать результат в тригонометрической и показательной формах.
и записать результат в тригонометрической и показательной формах. в тригонометрической форме, для чего определим его модуль и аргумент
в тригонометрической форме, для чего определим его модуль и аргумент ,
,

 ,
,  .
. ,
,  .
. ,
,  ,
,  ,
,  к главному значению, получим
к главному значению, получим

 б)
б)  в)
в)  ,
, , д)
, д)  , е)
, е) 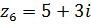 .
. , б)
, б)  .
. , б)
, б)  , в)
, в)  .
. .
. (
( – действительное,
– действительное,  ).
). .
. .
. .
.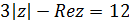 .
. ,
,  .
. .
. .
. и
и  .
. .
. .
. ; б)
; б)  .
. ;
;  ;
;  ,
,  ;
; .
. .
. .
. от
от  до
до  .
.