Выпуклый симплексный метод Зангвилла (АОИ)

Рассмотрим алгоритм выпуклого симплексного метода Зангвилла для решения задачи минимизации f(x) при условии

 

А(1,1)Х(1,0) = b(1,0);

Х(1,0) ³ 0.

Начальный этап.

Выбрать точку Х₁, для которой

АХ₁ = b;

Х₁ ³ 0.

Положить k = 1 и перейти к основному этапу.

 

 

Основной этап.

Шаг 1. При заданном X_k определить I_k – множество индексов m

наибольших (арифметически,т.е. не по модулю) компонент вектора X_k;

 

B(1,1) = {a_j½j Î I_k};

N(1,1) = {a_j½j Ï I_k}; (3)

r(0,1) = Ñf(X_k)^T - Ñ_bf(X_k)^T ×B^-1 × A; (4)

 

a = max{-r_j½выбирать из r_j £ 0}; (5)

b = max{xiri½ выбирать из r_j ³ 0}; (6)

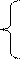n = индекс, для которого a = -r_n; (7)

или (!!!)

индекс, для которого b = x_nr_n (8)

 

 

Если a = b = 0, то остановиться.

Если a > b, то вычислить d_N в соответствии с (7) и (9):

 

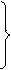
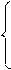0, если j Ï I_k; j ¹ n

d_j = (9)

1, если j Ï I_k; j = n,

т.е.для данного случая(a > b) из множества N только

одному направлению(j = n) придается значение 1,

остальным 0.

 

 

Если a < b, то вычислить d_N по формулам (8), (10):

 

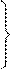
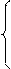0, если j Ï I_k; j ¹ n

d_j = -1, если j Ï I_k; j = n (10),

т.е.для данного случая(a < b) из множества N только

одному направлению(j = n) придается значение(-1),

остальным 0.

 

 

Если a = b ¹ 0, то вычислить d_N либо по формулам (7), (9), либо по формулам (8), (10).

В любом случае определить d_B в соответствии с (11)

d_B = B^-1 × N × dN (11)

И перейти к шагу 2.

Шаг 2

Минимизировать f(x_k + ld_k) при условии 0 £ l £ l_max,

где

 

Пусть l_k - оптимальное решение этой задачи.

Положить

x_k+1 = x_k + l_kd_k,

(заменить k на k+1,т.е.задать новые начальные условия поиска)

И перейти к шагу 1.

Пример

Минимизировать

I = 2x₁² + 2x₂² – 2x₁x₂ – 4x₁ – 6x₂

 

при условиях

 

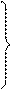x1 + x2 + x3 = 2,

x1 + 5x2 + x4 = 5,

x1, x2, x3, x4 ³ 0.

 

 

Решим задачу выпуклым симплексным методом Зангвилла.

 

Возьмем в качестве начальной точки x₁ = (0;0;2;5)^T. Заметим, что

Ñf(x) = (4x₁ – 2x₂ – 4; 4x₂ – 2x₁ – 6; 0; 0)^T.

 

Итерация 1

Поиск направления минимизации.

В точке х₁ имеем r(0,1) =Ñf(x₁)={-4; -6; 0; 0}.

Соответственно алгоритму I₁ = {3,4}, поэтому

 

.

 

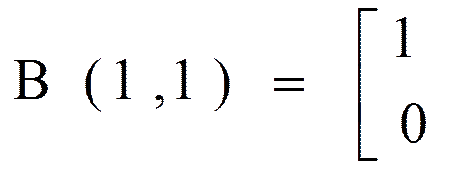
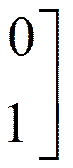
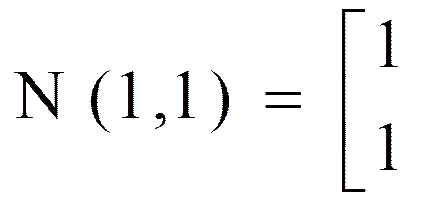
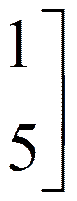Приведенный градиент вычисляется в соответствии с (4):

r^T = (-4; -6; 0; 0).

 

В соответствии с (5) получаем

a = max{-r₁, -r₂, -r₃, -r₄} = -r₂ = 6.

Из (6) имеем b = max{x₃ r₃, x₄r₄} = 0

ИТАК, a > b,

И, следовательно, из (7) получаем, что

n = 2.

Построение направления проводится по формулам (9) и (11).

Из (9) имеем d_N^T = (d₁, d₂) = (0;1), а из (11) следует, что

d_B^T = {d₃, d₄} = =(-1; -5).

Линейный поиск из точки х₁(0,0,2,5)^Т осуществляется по направлению d₁ = {0;1;-1;-5}^T. Максимальное значение l, для которого точка x₁ + ld₁ допустима, определяется по формуле:

 

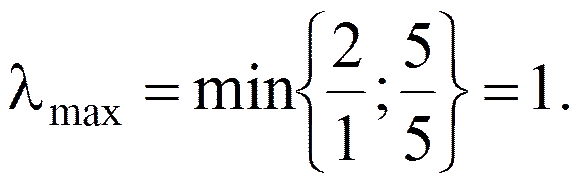
Кроме того, имеем f(x₁ + ld₁) = 2l² - 6l. Следовательно, нужно решить задачу минимизации 2l² - 6l при условии

0 £ l £ 1. Оптимальным решением является l =1, так что х₂ = х₁ + ld₁ = (0,1,1,0)^T.

Итерация 2

 

 

Поиск направления минимизации.

В точке х₂ = (0, 1, 1, 0) множество I₂ = {2;3},

Т.е.

 

 

,

 

 

 

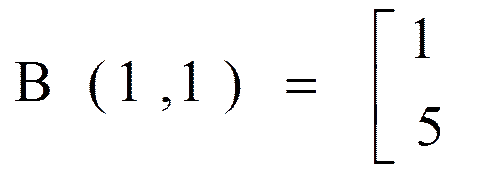
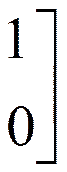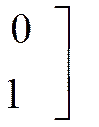
Ñf(x₂) = (-6; -2; 0; 0)^T.

 

 

При этом приведенный градиент (4)

 

 

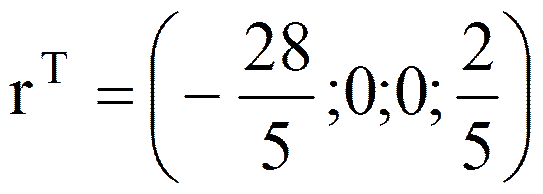
В соответствии с (5) и (6) имеем

a = max{-r₁, -r₂, -r₃} = -r₁₌

;

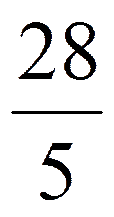b = max{x₂r₂; x₃r₃; x₄r₄} = 0,

т.е. a > b, и тогда получаем

согласно (7): n = 1.

 

 

Согласно (9), (11) имеем

d_N^T = (d₁, d₄) = (1; 0).

 

 

 

 

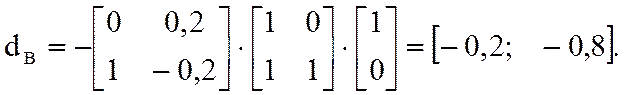
Тогда d₂ = (1; -0,2; -0,8; 0).

Линейный поиск.

Из точки x₂ = (0,1,1,0)^T по направлению

d₂ = (1, -0,2; -0,8; 0)^T.

Максимальное значение l, для которого точка (x₂ + ld₂) допустима, определяется по формуле (32):

.

 

 

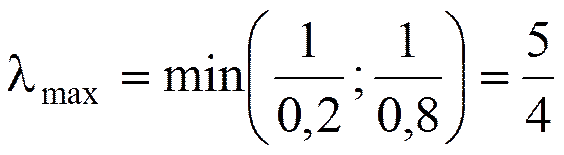Кроме того, f(x₂ + xd₂) = 2,48l² – 5,6l - 4.

Следовательно, нужно решить следующую задачу: минимизировать 2,48l² – 5,6l - 4 при условии 0 £ l £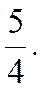

Оптимальное решение равно l₂= ,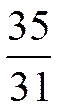

т.е. x₃ = x₂ + l₂d₂ =

Итерация 3

Поиск направления.

В точке x₃ множество I₃ = (1,2), т.е.

 

 

 

 

 

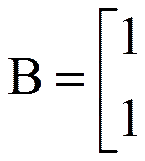
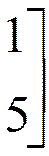
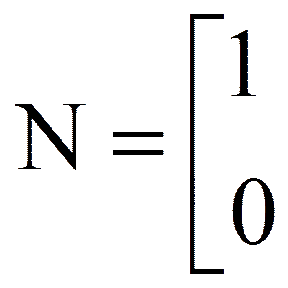
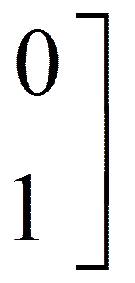
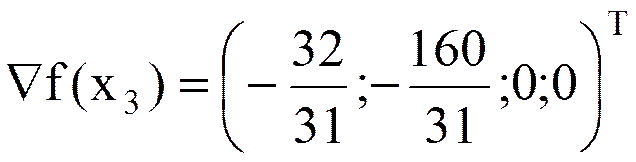
Из (4) получаем r^T = (0;0;0;1). В этом случае a = max{-r₁, -r₂, -r₃} = 0,

b = max(x₁r₁; x₂r₂; x₃r_3; x₄r₄) = 0.

Таким образом, точка x₃ оптимальна. Оптимальное значение целевой функции

 

I = -7,16.

Для практических расчетов целесообразно сочетать метод Зангвилла и метод ДФП.Метод Зангвилла более прост для определения направления минимизации, а для поиска минимума в выбранном направлении удобен метод ДФП.