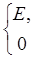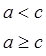Д о к а з а т е л ь с т в о. Легко проверить, что
E (f ³ a) = 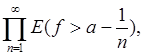
откуда следует измеримость множества E (f ³ a). Измеримость прочих множеств вытекает из соотношений:
E (f = a) = E(f ³ a) – E(f > a), E(f £ a) = E – E(f > a),
E (f < a) = E – E (f ³ a).
Замечание. Легко показать, что если хоть одно из множеств
E (f ³ a), E (f £ a), E (f < a)
оказывается измеримым при всяком а, то функция f (x) измерима на множестве Е (которое также предполагается измеримым).
Действительно, тождество 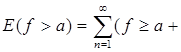
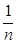 ) показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные утверждения. Таким образом, в определении измеримой функции можно заменить множество Е (f>a) любым из множеств (1).
) показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные утверждения. Таким образом, в определении измеримой функции можно заменить множество Е (f>a) любым из множеств (1).
Теорема 7. Если функция f (x), заданная на множестве Е, измерима, а k конечное число, то измеримы и функции 1) f (x) + k, 2) kf (x), 3) ç f (x) ç, 4) f 2 (x), и если f (x) ¹ 0, то измерима и функция 5) 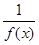 .
.
Д о к а з а т е л ь с т в о. 1) Измеримость функции f(x) + k вытекает из соотношения Е (f+ k >a) = E (f>a- k).
2) Измеримость функции kf(x) при k =0 следует из теоремы 5. Для прочих k измеримость следует из очевидных соотношений
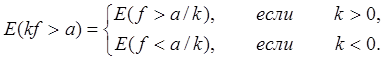
3) Функция çf(x) ç измерима потому, что
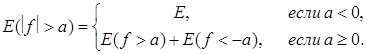
4) Аналогично, из того, что
E (f2 > a) = 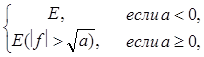
вытекает измеримость функции f 2 (x).
5) Наконец, при f(x) ¹ 0 имеем
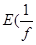 > a) =
> a) = 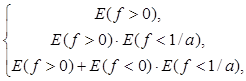
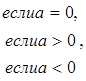
откуда и следует измеримость 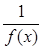 .
.
Теорема 8. Функция f (x), заданная и непрерывная на сегменте Е= 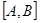 , измерима.
, измерима.
Д о к а з а т е л ь с т в о. Прежде всего установим, что множество
F = E (f£ a)
замкнуто. Действительно, если x0 есть предельная точка этого множества и xn®x0 (x n ÎF), то f(xn) £a и, в силу непрерывности f(x), будет f(x0 ) £a, т.е. x0 ÎF, что и устанавливает замкнутость множества F.
Но тогда множество Е (f>а) = Е – Е(f£а) измеримо, и теорема доказана.
Из самого определения измеримой функции следует, что функция, заданная на неизмеримом множестве, неизмерима.
Однако легко обнаружить существование неизмеримой функции, заданной на измеримом множестве.
Определение 4. Пусть М есть подмножество сегмента Е = [А, В]. Функция jм (х), равная единице на множестве М и нулю на множестве Е–М, называется характеристической функцией множества М.
Теорема 9. Множество М и его характеристическая функция j м одновременно измеримы или нет.
Д о к а з а т е л ь с т в о. Если функция jM (х) измерима, то измеримость множества М вытекает из соотношения
М = Е (jм > 0).
Обратно, если М есть измеримое множество, то соотношения
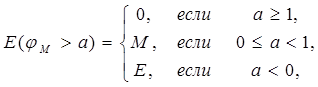
устанавливают измеримость функции jМ (х).
Отсюда, между прочим, весьма просто получаются примеры разрывных измеримых функций.
Но так как
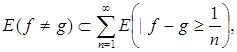
то f ~g, что и требовалось доказать.
Теоремы 2 и 3 показывают, что, желая восстановить свойство единственной предельной функции для сходимости по мере, мы должны были бы условиться считать эквивалентные функции за тождественные. Это обычно и делается в метрических вопросах теории функций, т.е. в тех вопросах, где все свойства функций изучаются с помощью меры множеств, на которых функция обладает или не обладает тем или другим свойством. В интегральном исчислении мы надем много примеров подобного подхода к вещам.
Хотя сходимость по мере общее сходимости почти везде, имеет место все же следующая теорема.
Теорема 4 (Ф.Рисс). Пусть { fn (x)} последовательность функций, которая сходится по мере к функции f (x). В таком случае существует подпоследовательность
fn1(x), fn2(x), fn3(x),... (n1<n2<n3<...),
сходящаяся к функции f (x) почти везде.
Д о к а з а т е л ь с т в о. Возьмем последовательность положительных чисел s1>s2>s3>¼, для которой lim sk=0.
Пусть, далее, h1+h2+h3+¼ (hk>0) есть сходящийся положительный ряд.
Теперь мы можем построить требуемую последовательность индексов
n1 < n2 < n3 <... (*)
следующим образом: обозначим через n1 натуральное число, для которого
mE(½fn1-f½³s1)<h1.
Такое число обязательно существует, ибо
mE(½fn-f½³s1)®0 при n®¥.
Затем через n2 обозначим то натуральное число, для которого
mE(½fn2-f½³s2)h2, n2>n1.
Вообще через nk мы обозначаем такое число, что
mE(½fnk-f½³sk)< hk, nk>nk-1.
Последовательность (*), таким образом, построена.
Теперь установим, что почти везде на множестве E будет
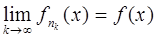 (**)
(**)
Действительно, пусть
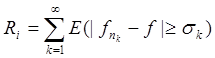 ,
, 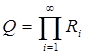 .
.
Так как R1ÉR2ÉR3É..., то (теорема 12)
mRi®mQ
C другой стороны, очевидно, что 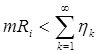 так что mRi®0 и, стало быть, mQ=0.
так что mRi®0 и, стало быть, mQ=0.
Остается проверить, что соотношение (**) имеет место для всех x из множества E - Q.
Пусть x0 Î E - Q. Тогда x0 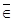 Rio. Иначе говоря, при k ³ i0
Rio. Иначе говоря, при k ³ i0
x0 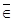 E(|fnk-f|³sk),
E(|fnk-f|³sk),
и, следовательно,
|fnk(x0) – f(x0)|<sk, (k ³ i0)
и, поскольку sk®0, ясно, что fnk(x0) ®f(x0).
Теорема доказана.
Теорема Лебега дала повод к установлению понятия сходимости по мере. С другой стороны, с помощью этой же теоремы можно установить весьма важную теорему Д.Ф.Егорова.
Теорема 5 (Д.Ф.Егоров). Пусть на измеримом множестве Е задана последовательность измеримых и почти везде конечных функций f 1 (x), f 2 (x), f 3 (x), …, почти везде сходящаяся к измеримой и почти везде конечной функции f (x):
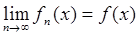
В таком случае, для любого d >0 существует такое измеримое множество Е d 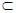 Е, что:
Е, что:
1) mE s > mE - d;
2) на множестве E d стремление(*) происходит равномерно.
Д о к а з а т е л ь с т в о. При доказательстве теоремы Лебега было установлено, что при любом s >0 будет
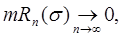 (1)
(1)
где 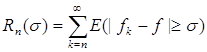 .
.
Но легко видеть, что
E (|f-y| ³ s) Ì E (f ¹ g) + E (|g-y| ³ s),
Так что функция y(x) решает задачу.
Следствие. Для всякой измеримой и почти везде конечной функции f (x), заданной на сегменте [ a, b ], существует последовательность непрерывных функций y n (x), сходящаяся по мере к функции f (x).
Определение и простейшие свойства измеримой функции
Если каждому x из множества E поставлено в соответствие некоторое число f(x), то мы будем говорить, что на множестве E задана функция f(x). При этом мы допускаем и бесконечные значения функции, лишь бы они имели определенный знак, т.е. вводим «несобственные» числа -  и +
и +  . Эти числа связаны между собой и с любым конечным числом a неравенствами
. Эти числа связаны между собой и с любым конечным числом a неравенствами
-  <a<+
<a<+  ,
,
и мы устанавливаем для них следующие законы действий:
+  ±a=+
±a=+  , +
, +  +(+
+(+  )=+
)=+  , +
, +  -(-
-(-  )=+
)=+  ,
,
-  ±a=-
±a=-  , -
, -  +(-
+(-  )=-
)=-  , -
, -  -(+
-(+  )=-
)=-  ,
,
½+  ½=½-
½=½-  ½=+
½=+  , +
, +  ×a=a×(+
×a=a×(+  )=+
)=+  ,
,
-  ×a=a×(-
×a=a×(-  )=-
)=-  , если a>0,
, если a>0,
+  ×a=a×(+
×a=a×(+  )=-
)=-  ,
,
-  ×a=a×(-
×a=a×(-  )=+
)=+  , если a<0
, если a<0
0×(±  )=(±
)=(±  )×0=0,
)×0=0,
(+  )×(+
)×(+  )=(-
)=(-  )×(-
)×(-  )=+
)=+  ,
,
(+  )×(-
)×(-  )=(-
)=(-  )×(+
)×(+  )=-
)=-  ,
,
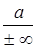 =0.
=0.
Здесь a обозначает вещественное конечное число. Символы
+¥-(+¥), -¥-(-¥), +¥+(-¥), -¥+(+¥).
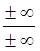 ,
, 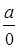
мы считаем лишенными смысла.
Имея дело с функцией f (x), заданной на множестве E, мы будем символом
E(f>a)
обозначать множество тех x из множества Е, для которых выполнено неравенство f(x)>а.
Аналогичным образом вводятся символы
Е(f³а), Е(f=а), Е(f£а), Е(а<f£b)
и т.п. Если множество, на котором задана функция f(x), обозначено какой-либо другой буквой, например А или В, то мы соответственно будем писать
А(f>а), В(f>а)
и т.п.
Определение 1. Функция f(x), заданная на множество Е, называется измеримой, если измеримо это множество Е и если при любом конечном а измеримо множество
Е(f>а).
В связи с тем, что здесь речь идет о множествах, измеримых в смысле Лебега, часто (желая подчеркнуть именно это обстоятельство) говорят об измеримой (L) функции. Если же Е и все множества Е(f>а) измеримы (В), то и f(x) называется измеримой (В) функцией.
Теорема 1. Всякая функция, заданная на множестве меры нуль, измерима.
Это утверждение очевидно.
Теорема 2. Пусть f (x) есть измеримая функция, заданная на множестве Е. Если А есть измеримое подмножество Е, то f (x), рассматриваемая только для x ÎА, измерима.
Действительно, А(f>а) =А×Е (f>а).
Теорема 3. Пусть f (x) задана на измеримом множестве Е, представимом в форме суммы конечного числа или счетного множества измеримых множеств Е k:
E = 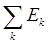 ×
×
Если f (x) измерима на каждом из множеств ER ., то она измерима и на Е.
В самом деле, E(f>a)= 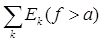 .
.
Определение 2. Две функции f(x) и g(x), заданные на одном и том же множестве Е, называются эквивалентными, если
mE (f¹g)=0
Обозначать эквивалентность функций f(x) и g(x) принято так:
f (x) ~g(x).
Определение 3. Пусть некоторое обстоятельство S имеет место для всех точек какого-нибудь множества Е, кроме точек, входящих в подмножество Е0 множества Е. Если mЕ0 = 0, то говорят, что S имеет место почти везде на множестве Е, или почти для всех точек Е.
В частности, множество исключительных точек Е0 может быть и пустым.
Теперь можно сказать, что две функции, заданные на множестве Е, эквиваленты, если они ровны почти везде на Е.
Теорема 4. Если f (х) есть измеримая функция, заданная на множестве Е, а g (x) ~ f (x), то g (x) также измерима.
Д о к а з а т е л ь с т в о. Пусть А = Е (f ¹ g), B = E – A. Тогда mA = 0, так что В измеримо. Значит функция f(x) измерима на множестве В. Но на множестве В функции f(x) и g(x) неотличимы, так что g(x) измерима на В. Поскольку g(x) измерима и на А (ибо mA = 0), она измерима на Е = А + В.
Теорема 5. Если для всех точек измеримого множества Е будет f (x) = c, то функция f (x) измерима.
Действительно,
E (f > a) = 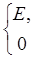
Заметим, что в этой теореме с может быть и бесконечным.
Функция f(x), заданная на сегменте [а, b], называется ступенчатой, если [а,b] разложить точками.
с0 = а< с1<с2<…<сn = b
на конечное число частей, в н у т р и которых (т.е. в интервалах (сk, ck + 1) при k = 0, 1, …., n –1) функция f(x) постоянна. Легко понять, что из теоремы 5 вытекает
Следствие. Ступенчатая функция измерима.
Теорема 6. Если f (x) есть измеримая функция, заданная на множестве Е, то при любом а измеримы множества
E (f ³ a), E (f = a), E (f £ a), E (f < a),



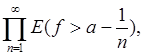
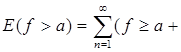
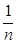 ) показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные утверждения. Таким образом, в определении измеримой функции можно заменить множество Е (f>a) любым из множеств (1).
) показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные утверждения. Таким образом, в определении измеримой функции можно заменить множество Е (f>a) любым из множеств (1).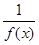 .
.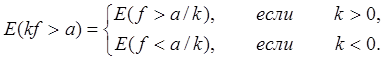
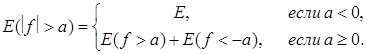
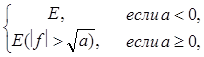
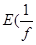 > a) =
> a) = 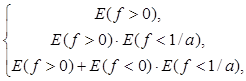
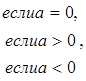
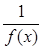 .
.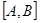 , измерима.
, измерима.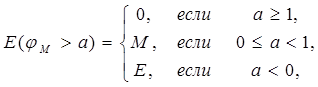
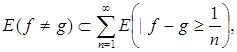
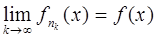 (**)
(**)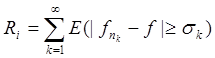 ,
, 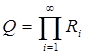 .
.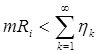 так что mRi®0 и, стало быть, mQ=0.
так что mRi®0 и, стало быть, mQ=0.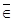 Rio. Иначе говоря, при k ³ i0
Rio. Иначе говоря, при k ³ i0 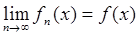
 Е, что:
Е, что: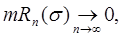 (1)
(1)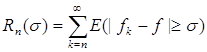 .
. и +
и + 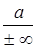 =0.
=0.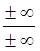 ,
, 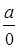
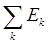 ×
×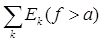 .
.