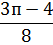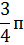Введение
В данном учебно-методическом комплексе рассматривается один из главных разделов математического анализа – определенный интеграл и его применение.
Эта работа может быть использована, как студентами-очниками, так и студентами-заочниками для лучшего усвоения данной темы. Но данное пособие не заменит, ни один из учебников по высшей математике, так как в них материал изложен более подробно.
Актуальность данной темы, подчеркивает все вышесказанное.
Цель исследования – систематизация и обобщение материала по теме «Определенный интеграл и его приложения», и создание на основе данного материала учебно-методического комплекса.
Объекты исследования – определенный интеграл, его свойства и методы вычисления, а так же приложения определенного интеграла (вычисление площадей плоских фигур, объемов тел вращений, длин дуг кривых, площадей поверхности).
Задачи исследования:
- анализирование теоретического материала по теме «Определенный интеграл и его применение»;
- составление практического материала по данной теме.
Структура выпускной квалификационной работы следующая:
- в первой главе рассматриваются сведения об определенном интеграле, и основные свойства определенного интеграла;
- во второй главе говорится о методах вычисления определенного интеграла: формула Ньютона-Лейбница, замена переменных, интегрирование по частям, а так же приведены примеры;
- третья глава посвящена приложениям определенного интеграла: вычисление площадей, объемов тел вращения и т.д.
Также ставится задача помочь студенту усвоить один из самых сложных разделов курса математического анализа «Определенный интеграл и его приложения».
.
Историческая справка
Понятие интеграла и интегрального исчисления возникло из потребности вычислять площади любых фигур, поверхностей и объемов тел.
Первое теоретического обобщение и обоснование методов вычисления площадей и объемов, где неявно использовались предельные переходы, сформулировал греческий математик Евдокс Книдски, его метод также называли методом исчерпывания.
Понятие производной, дифференциала и интеграла, как и весь математический анализ, основываются на разработанном в XIX в. методе пределов (или на методе бесконечно малых). С конце XVIII в. в Европе образовались 2 крупные математические школы. Главой одной крупнейшей школы был немецкий ученый Готфрид Вильгельм фон Лейбниц, а вторую школу возглавил Исаак Ньютон. Обе школы привели к созданию дифференциального и интегрального исчисления.
В своих трудах Л. Эйлер излагал многочисленные приемы вычисления не только неопреденного интеграла, но и определенного, применяя и развивая новые методы интегрирования, как например метод интегрирования по параметру. Он вычислил много труднейших определенных интегралов, к примеру:

И открыл ряд новых важных интегралов:
бета-функцию:

гамма-функцию:

В начале XIX в. французский математик Огюстен Луи Коши начал реформу интегрального исчисления, при которой определенный интеграл, рассматривался, как предел интегральной суммы. Коши выдвинул одно из важнейших понятий, при этом он пользовался символом, который предложил Джозеф Фурье.

Благодаря Коши, этот символ вошел в общее употребление и сохранился до сих пор.
Термин «определенный интеграл» предложил в 1779 г. Пьер Симон Лаплас.
В развитие интегрального исчисления в XIX в. приняли важнейшее участие и русские ученые: М. В. Остроградский, предложил оригинальный прием интегрирования рациональных дробей, позволяющий алгебраически выделить рациональную часть интеграла. Математик В. Я. Буняковский открыл широко применяемое неравенство:
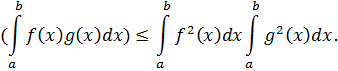
Общая теория интеграла связана с развитием теории множеств и теории функций действительной переменной.
Формула Ньютона-Лейбница
В предыдущем пункте показано, что функция f(x), непрерывная на отрезке [a;b], имеет первообразную. В качестве первообразной можно взять следующую функцию

то есть интеграл с переменным верхним пределом.
Теперь поставим обратную задачу, то есть зная одну из первообразных Ф(х) функции f (x) на [ a; b ], вычислить определенный интеграл от f(x) на этом отрезке или найти определенный интеграл по известному неопределенному.
Следующая теорема показывает основную формулу интегрального исчисления, то есть формулу Ньютона-Лейбница (выражает определенный интеграл, через неопределенный).
Теорема.
Если F (x) является первообразной непрерывной функции f (x), то справедлива формула:

Доказательство.
По теореме Барроу  - первообразная функции f (x), поэтому F (x) и
- первообразная функции f (x), поэтому F (x) и  отличаются на константу C, то есть
отличаются на константу C, то есть

Пусть x = a, тогда 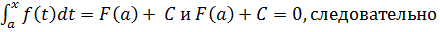
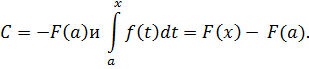
Но приняв в этом равенстве x = b, получается формула Ньютона – Лейбница:

Символ  называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:
называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:

Можно записать в виде:

Пример 1.

Пример 2.
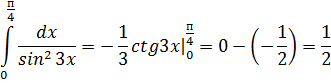
Пример 3.
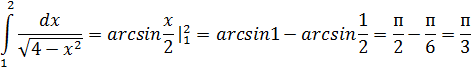
Замена переменных
Теорема.
Рассмотрим

где f (x) непрерывна на [a,b]. Введем новую функцию 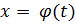 , заданную на
, заданную на  и удовлетворяющую следующим условиям:
и удовлетворяющую следующим условиям:
1.  непрерывны на
непрерывны на  ;
;
2. может быть определена сложная функция  ;
;
3.  .
.
Тогда:

Доказательство.
Для проверки можно заметить, что если F(x) является первообразной для f(x), то очевидно 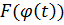 - первообразная для подынтегральной функции в правой части полученной формулы, значит:
- первообразная для подынтегральной функции в правой части полученной формулы, значит:
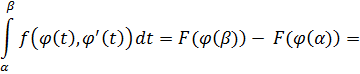

Пример 1.

Сделаем замену  . Найдем
. Найдем 
 и вычислим новые пределы интегрирования
и вычислим новые пределы интегрирования  Тогда:
Тогда:

Пример 2.

Сделаем замену  . Вычислим новые пределы интегрирования
. Вычислим новые пределы интегрирования  Тогда:
Тогда:
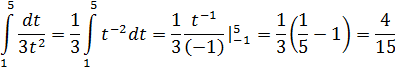
Интегрирование по частям
Теорема.
Пусть функции u(x) и v(x) дифференцируемы на отрезке [a;b], то справедлива следующая формула:

Или в компактной форме можно записать:

Эта формула называется формулой интегрирования по частям для определенного интеграла.
Доказательство.
Применим формулу Ньютона – Лейбница и формулу интегрирования по частям в неопределенном интеграле:


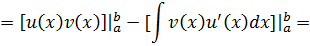

Теорема доказана.
Пример 1.Вычислить:

Решение: пусть  , тогда
, тогда  . По формуле интегрирования по частям:
. По формуле интегрирования по частям:
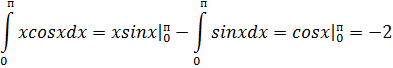
Пример 2. Найти:
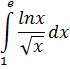
Решение:  , тогда
, тогда  , и по формуле интегрирования по частям:
, и по формуле интегрирования по частям:


Интеграла
Заключение
В данной работе были рассмотрены основные определения,свойства, теоремы, связанные с изучением темы «Определенный интеграл и его приложения».
Решение задач с использованием приложений определенного интеграла является одним из сложных разделов математического анализа.
Считаю, что задачи, поставленные перед собой выполнила, а именно:
- анализирование теоретического материала по теме «Определенный интеграл и его применение»;
- составление практического материала по данной теме.
Данную работу можно использовать как методические рекомендации для студентов, а также она может помочь преподавателям высшей математики для проведения контрольных, самостоятельных работ.
Приложения
| Таблица основных интегралов:
| Таблица основных интегралов:
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
Контрольная работа
Вариант 1.
1. Вычислить интегралы

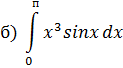

2. Вычислить площадь фигуры, ограниченной графиками функций:

3. Вычислить длину дуги кривой

4. а) Найти объем тела, ограниченного поверхностями

б) Найти объем тела, образованного при вращении вокруг оси Ох фигуры, ограниченной линиями
Вариант 2.
1. Вычислить интегралы
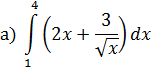

в) 
2. Вычислить площадь фигуры, ограниченной линиями:

3. Вычислить длину дуги кривой:

4. а) Найти объем тела, ограниченного поверхностями

б) Найти объем тела, образованного при вращении вокруг оси Ох фигуры, ограниченной линиями

Вариант 3.
1. Вычислить интегралы
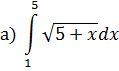


2. Вычислить площадь фигуры:
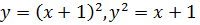
3. Найти длину дуги всей кривой
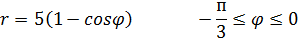
4. а) Найти объем тела, ограниченного поверхностями
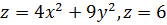
б) Найти объем тела, образованного при вращении вокруг оси … фигуры, ограниченной линиями

Вариант 4.
1. Вычислить интегралы



2. Вычислить площадь фигуры, ограниченной линиями:

3. Вычислить длину дуги кривой

4. а) Найти объем тела, ограниченного поверхностями
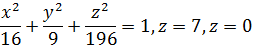
б) Найти объем тела, образованного при вращении вокруг оси Ох фигуры, ограниченной линиями
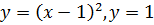
Вариант 5.
1. Вычислить интегралы

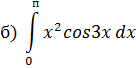
в) 
2. Вычислить площадь фигуры:

3. Вычислить длину дуги кривой

4. а) Найти объем тела, ограниченного поверхностями

б) Найти объем тела, образованного при вращении вокруг оси Оу фигуры, ограниченной линиями

Ответы
| Вариант 1
| Вариант 2
| Вариант 3
| Вариант 4
| Вариант 5
|
А) 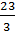 Б)
Б)  В)
В) 
| А)21
Б) 1
В)2
| А)  Б)
В)
Б)
В) 
| А)  Б)
Б) 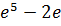 В)
В) 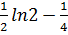
| А)  Б)
Б)  В)
В) 
|

| 
| 
| 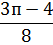
| 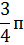
|

| 
| 
| 
| 
|
А) 72
Б) 
| А)п
Б) 
| А)3п
Б) 
| А)77п
Б) 
| А) 72п
Б) 
|
Список литературы
1. Баврин И.И. Высшая математика: Учеб. для студентов естественнонаучных специальностей педагогических вузов. 3-е изд., стереотип. М.:Изд. центр «Академия», 2003. 616 с.
2. Садовичая И. В., Хорошилова Е. В. – Математический анализ: определенный интеграл В 2 ч. Часть 1: учеб. пособие для академического бакалавриата / 2-е изд., перераб. и доп. – М.: Издательство Юрайт, 2018. – 242 с. – (Серия: Бакалавр, Академический курс).
3. Берман Г. Н.: Сборник задач по курсу математического анализа: У. пособие – 22-е изд., перераб. – СПб, Изд-во «Профессия», 2001. – 432 с.
4. Ильин В.А. Математический анализ: Учебник:В 2 ч. Ч.2. МГУ им. Ломоносова 2-е издание. М.:Проспект: Издательство Московского университета, 2004. 353с.
5. Кудряв цев Л.Д. Сборник задач по математическому анализу. Том 2. Интегралы. Ряды: Учебное пособие под ред. Л.Д.Кудрявцева, 2-е изд. М.:ФИЗМАТЛИТ, 2003. 504с.
6. В.А. Математический анализ: Учебник:В 2 ч. Ч.2. МГУ им. Ломоносова 2-е издание. М.:Проспект: Издательство Московского университета, 2004. 353с.
7. Задачи и упражнения по математическому анализу для втузов под редакцией Б.П. Демидовича. Астрель, 2004, 495 с.
8. Давыдо в Н.А. сборник задач по математическому анализу. Учебник для студентов физ.-мат. факультетов педагогических институтов Издание 4-е., доп. М., «Просвещение», 1973.256.
9. Берман Г.Н. Сборник задач по курсу математического анализа. Изд. 20-е Наука, РГМФЛ. 1985. 384с.
10. Чернен ко В.Д. Высшая математика в примерах и задачах: Учеб. Пособие для вузов. В 3 т.: Т.1. СПб.:Политехника 2003. 703с.
Введение
В данном учебно-методическом комплексе рассматривается один из главных разделов математического анализа – определенный интеграл и его применение.
Эта работа может быть использована, как студентами-очниками, так и студентами-заочниками для лучшего усвоения данной темы. Но данное пособие не заменит, ни один из учебников по высшей математике, так как в них материал изложен более подробно.
Актуальность данной темы, подчеркивает все вышесказанное.
Цель исследования – систематизация и обобщение материала по теме «Определенный интеграл и его приложения», и создание на основе данного материала учебно-методического комплекса.
Объекты исследования – определенный интеграл, его свойства и методы вычисления, а так же приложения определенного интеграла (вычисление площадей плоских фигур, объемов тел вращений, длин дуг кривых, площадей поверхности).
Задачи исследования:
- анализирование теоретического материала по теме «Определенный интеграл и его применение»;
- составление практического материала по данной теме.
Структура выпускной квалификационной работы следующая:
- в первой главе рассматриваются сведения об определенном интеграле, и основные свойства определенного интеграла;
- во второй главе говорится о методах вычисления определенного интеграла: формула Ньютона-Лейбница, замена переменных, интегрирование по частям, а так же приведены примеры;
- третья глава посвящена приложениям определенного интеграла: вычисление площадей, объемов тел вращения и т.д.
Также ставится задача помочь студенту усвоить один из самых сложных разделов курса математического анализа «Определенный интеграл и его приложения».
.
Историческая справка
Понятие интеграла и интегрального исчисления возникло из потребности вычислять площади любых фигур, поверхностей и объемов тел.
Первое теоретического обобщение и обоснование методов вычисления площадей и объемов, где неявно использовались предельные переходы, сформулировал греческий математик Евдокс Книдски, его метод также называли методом исчерпывания.
Понятие производной, дифференциала и интеграла, как и весь математический анализ, основываются на разработанном в XIX в. методе пределов (или на методе бесконечно малых). С конце XVIII в. в Европе образовались 2 крупные математические школы. Главой одной крупнейшей школы был немецкий ученый Готфрид Вильгельм фон Лейбниц, а вторую школу возглавил Исаак Ньютон. Обе школы привели к созданию дифференциального и интегрального исчисления.
В своих трудах Л. Эйлер излагал многочисленные приемы вычисления не только неопреденного интеграла, но и определенного, применяя и развивая новые методы интегрирования, как например метод интегрирования по параметру. Он вычислил много труднейших определенных интегралов, к примеру:

И открыл ряд новых важных интегралов:
бета-функцию:

гамма-функцию:

В начале XIX в. французский математик Огюстен Луи Коши начал реформу интегрального исчисления, при которой определенный интеграл, рассматривался, как предел интегральной суммы. Коши выдвинул одно из важнейших понятий, при этом он пользовался символом, который предложил Джозеф Фурье.

Благодаря Коши, этот символ вошел в общее употребление и сохранился до сих пор.
Термин «определенный интеграл» предложил в 1779 г. Пьер Симон Лаплас.
В развитие интегрального исчисления в XIX в. приняли важнейшее участие и русские ученые: М. В. Остроградский, предложил оригинальный прием интегрирования рациональных дробей, позволяющий алгебраически выделить рациональную часть интеграла. Математик В. Я. Буняковский открыл широко применяемое неравенство:
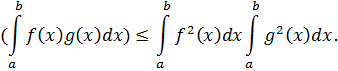
Общая теория интеграла связана с развитием теории множеств и теории функций действительной переменной.
Глава 1. Понятие определенного интеграла и его свойства.







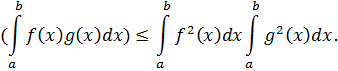


 - первообразная функции f (x), поэтому F (x) и
- первообразная функции f (x), поэтому F (x) и 
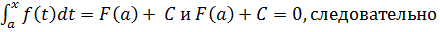
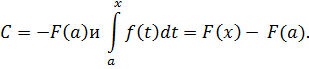

 называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:
называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:

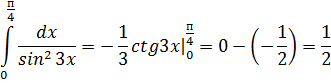
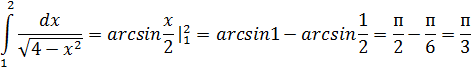

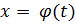 , заданную на
, заданную на  и удовлетворяющую следующим условиям:
и удовлетворяющую следующим условиям: непрерывны на
непрерывны на  ;
; .
.
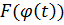 - первообразная для подынтегральной функции в правой части полученной формулы, значит:
- первообразная для подынтегральной функции в правой части полученной формулы, значит: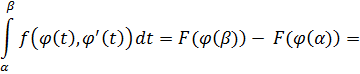


 . Найдем
. Найдем 
 и вычислим новые пределы интегрирования
и вычислим новые пределы интегрирования  Тогда:
Тогда:

 . Вычислим новые пределы интегрирования
. Вычислим новые пределы интегрирования  Тогда:
Тогда: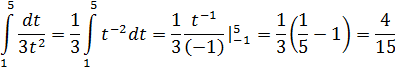




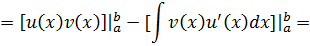


 , тогда
, тогда  . По формуле интегрирования по частям:
. По формуле интегрирования по частям: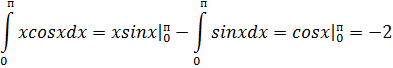
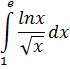
 , тогда
, тогда  , и по формуле интегрирования по частям:
, и по формуле интегрирования по частям:









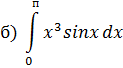




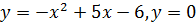
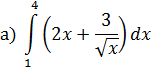






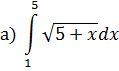


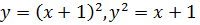
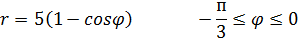
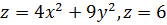






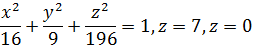
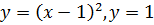

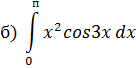





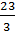 Б)
Б)  В)
В) 
 Б)
В)
Б)
В) 
 Б)
Б) 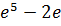 В)
В) 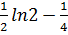
 Б)
Б)  В)
В)