Дополнение
Метод (принцип) математической индукции
Иногда, наблюдение указывает на проявление некоторой закономерности в зависимости от натурального  , начиная с некоторого. Естественно, появляется потребность доказать, что наблюдаемая закономерность проявляется при всех натуральных
, начиная с некоторого. Естественно, появляется потребность доказать, что наблюдаемая закономерность проявляется при всех натуральных  , начиная с некоторого известного номера. В этом случае часто применяется метод математической индукции.
, начиная с некоторого известного номера. В этом случае часто применяется метод математической индукции.
Этот метод эффективен, однако, сам по себе, не вскрывает причины проявления наблюдаемой закономерности, то есть сути явления.
1. Пусть логическое утверждение  верно при
верно при  .
.
2. Пусть из предположения, что  верно при
верно при 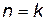 следует, что
следует, что  верно при
верно при  .
.
Тогда метод (принцип) математической индукции утверждает, что утверждение  верно при всех
верно при всех 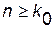 .
.
В самом деле, из 1,2 следует, что  - верно. Из 2) следует, что
- верно. Из 2) следует, что 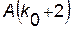 , так как
, так как  - верно. И т.д.
- верно. И т.д.
Пример. Доказать, что  .
.
При  , имеем:
, имеем: 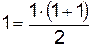 . Утверждение верно.
. Утверждение верно.
Пусть при  утверждение верно, т.е. равенство
утверждение верно, т.е. равенство  - верно.
- верно.
Тогда

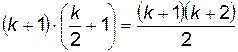 .
.
То есть утверждение верно и при  . Из принципа математической индукции, утверждение верно при всех
. Из принципа математической индукции, утверждение верно при всех  , a значит и при всех
, a значит и при всех  , так как тождество подразумевает, что
, так как тождество подразумевает, что  - натуральное число
- натуральное число
Замечание. Уже говорилось, что метод математической индукции не вскрывает сущности формулы или утверждения. В нашем примере  .
. 




 .
.
В этом решении уже вскрыта сущность формулы. (Здесь, далее, помещены сведения, которые применялись в решениях задач).
Алгебра
Основная теорема
Всякий многочлен  -й степени
-й степени 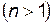 имеет
имеет  комплексных корней, то есть (при
комплексных корней, то есть (при  )
)
 .
.
Теорема Виета (обобщенная)
Если  , то
, то  ,
,  ,…,
,…, 
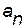 .
.
Теорема Безу
Всякий многочлен  -й степени, имеющий корень
-й степени, имеющий корень  без остатка разделится на
без остатка разделится на  .
.
Пример: 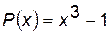 ;
; 

 , то есть
, то есть  делится без остатка на
делится без остатка на  .
.
Линейная алгебра
Матрицы и определители
 (здесь
(здесь  - определитель квадратной матрицы
- определитель квадратной матрицы  )
)
Свойства диагональных матриц
1. 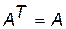
2. Если  , то
, то  - тоже диагональная матрица и
- тоже диагональная матрица и  .
.
3. Если  ,
, 
 , то
, то 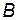 - тоже диагональная матрица и
- тоже диагональная матрица и  .
.
Ранг матрицы
Определение. Рангом матрицы называется число ее линейно независимых строк (столбцов).
Теорема 1.  (здесь
(здесь 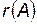 - ранг матрицы
- ранг матрицы  ).
).
Теорема 2. При умножении матрицы на невырожденную, ранг матрицы сохраняется.
Доказательство. Воспользуемся теоремой: 
 .
.
Пусть  .
. 
 . Имеем,
. Имеем,  .
.  . Отсюда
. Отсюда  . Аналогично доказывается, что
. Аналогично доказывается, что 
 . Теорема 2 доказана.
. Теорема 2 доказана.
Теорема 3. Перестановка  -й и
-й и  -й строки квадратной матрицы равносильно умножению слева на нее матрицы
-й строки квадратной матрицы равносильно умножению слева на нее матрицы



Прибавление к  -й строке матрицы ее
-й строке матрицы ее  -й строки, умноженной на число
-й строки, умноженной на число 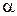 равносильно умножению слева на нее матрицы
равносильно умножению слева на нее матрицы


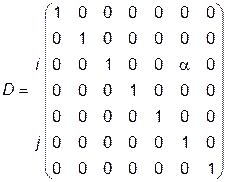
Умножение  -й строки матрицы на число
-й строки матрицы на число  равносильно умножению слева на нее матрицы
равносильно умножению слева на нее матрицы

Аналогичные утверждения для столбцов. Только умножать на эти же матрицы нужно справа.
Элементарные преобразования матрицы
Перечисленные операции со строками и столбцами называются элементарными преобразованиями.


 .
.
Доказательство. В самом деле, пусть в матрице  нужно переставить
нужно переставить  -ю и
-ю и  -ю строки (
-ю строки ( ).
).
Пусть матрица  получается из единичной матрицы сдвигом единицы в
получается из единичной матрицы сдвигом единицы в  -й и
-й и  -й строке следующим образом: в
-й строке следующим образом: в  -й строке единичной матрицы единица сдвигается на место
-й строке единичной матрицы единица сдвигается на место  -го столбца, а в
-го столбца, а в  -й строке единичной матрицы единица сдвигается на место
-й строке единичной матрицы единица сдвигается на место  -го столбца.
-го столбца.


 .
.
Тогда, по формуле умножения матриц, для квадратных матриц, имеем: если  , то
, то 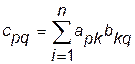 . Положим
. Положим 
Пусть  , тогда
, тогда 
= 
Это и значит, что матрица  получена из матрицы
получена из матрицы  перестановкой
перестановкой  -й и
-й и  -й строк.
-й строк.
Теперь пусть нужно к  -й строке матрицы
-й строке матрицы  прибавить
прибавить 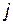 -ю строку, умноженную на число
-ю строку, умноженную на число 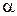 . Положим
. Положим
 , то есть матрица
, то есть матрица  имеет вид:
имеет вид:



 ,
,
Тогда 

Это и значит, что матрица  получена из матрицы
получена из матрицы  прибавлением к
прибавлением к  -й строке
-й строке  -ой строки, умноженной на число
-ой строки, умноженной на число 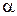 . Теперь, пусть нужно
. Теперь, пусть нужно  -ю строку матрицы
-ю строку матрицы 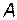 умножить на число
умножить на число 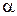 .
.
Положим
 . То есть
. То есть  имеет вид:
имеет вид:
 . Пусть
. Пусть 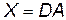 .
.
Тогда

 .
.
Это и значит, что матрица  получена из матрицы
получена из матрицы  умножением
умножением  -й строки матрицы
-й строки матрицы 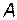 на число
на число 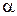 .
.
Аналогично доказывается, что те же операции со столбцами осуществляются умножением матрицы справа на эти же матрицы.
Пусть нужно переставить столбцы с номерами  и
и 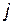 . Пусть
. Пусть  . Тогда, поскольку
. Тогда, поскольку
 , то
, то
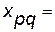
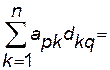
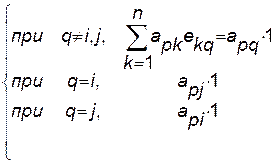
Это и значит, что матрица  получена перестановкой в матрице
получена перестановкой в матрице 
 -го и
-го и  -го столбца.
-го столбца.
Пусть теперь нужно в матрице 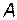 к
к  -му столбцу прибавить
-му столбцу прибавить 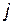 -й столбец, умноженный на число
-й столбец, умноженный на число 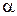 . Пусть
. Пусть  . Тогда, поскольку
. Тогда, поскольку
 .
.
Тогда


 . Это и значит, что в матрице
. Это и значит, что в матрице 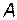 к
к  -му столбцу прибавили
-му столбцу прибавили  -й столбец, умноженный на число
-й столбец, умноженный на число 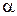 .
.
И, наконец, пусть теперь нужно  -й столбец матрицы
-й столбец матрицы  умножить на число
умножить на число 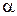 .
.
Пусть  .
.
Тогда 
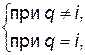
 .
.
Это и значит, что матрица  получена из матрицы
получена из матрицы  умножением
умножением  -го столбца на число
-го столбца на число 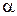 . Теорема 3 доказана.
. Теорема 3 доказана.
Замечание. Элементарными преобразованиями матрицы можно привести ее к диагональному виду так, чтобы на диагонали стояли либо единицы, либо нули. Количество единиц тогда является рангом матрицы.
Теорема Кэли
Квадратная матрица 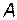 является корнем своего характеристического многочлена, то есть если
является корнем своего характеристического многочлена, то есть если 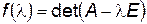 , то
, то 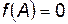 .
.
Например: 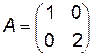 ,
, 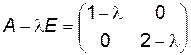 ,
, 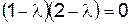 .
. 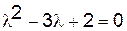 .
. 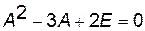 . Действительно,
. Действительно, 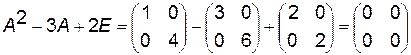 .
.
Линейные операторы
Определение. Отображение 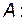
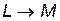 , где
, где 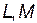 - векторные пространства, называется линейным оператором, если
- векторные пространства, называется линейным оператором, если
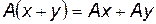 ,
, 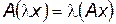 для всех
для всех 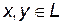 .
.
Теорема Штольца
Если 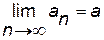 , то
, то 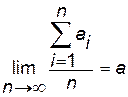 .
.
Теорема (принцип сжатых отображений):
Пусть 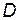 - одно из следующих множеств:
- одно из следующих множеств: 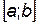 ,
, 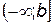 ,
, 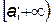 .
.
Пусть при всех 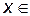
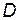 :
: 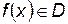 , функция
, функция 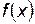 непрерывна, дифференцируема и выполняется неравенство
непрерывна, дифференцируема и выполняется неравенство 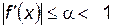 .
.
Тогда, если при некотором 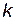 ,
, 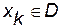 , то рекуррентная последовательность
, то рекуррентная последовательность 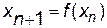 имеет пределом некоторое
имеет пределом некоторое 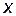 , причем
, причем 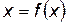 и
и 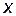
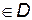 .
.
Непрерывность
Определения. Пусть функция 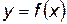 определена в точке
определена в точке 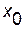 и в некоторой окрестности этой точки. Функция
и в некоторой окрестности этой точки. Функция 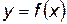 называется непрерывной в точке
называется непрерывной в точке 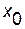 , если существует предел функции в этой точке и он равен значению функции в этой точке, то есть
, если существует предел функции в этой точке и он равен значению функции в этой точке, то есть 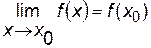 .
.
Функция 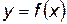 называется непрерывной в интервале (
называется непрерывной в интервале (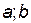 ), если она непрерывна в каждой точке этого интервала.
), если она непрерывна в каждой точке этого интервала.
Функция 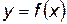 называется непрерывной на отрезке [
называется непрерывной на отрезке [ 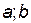 ], если она непрерывна в интервале (
], если она непрерывна в интервале (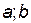 ) и в точке
) и в точке 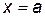 непрерывна справа (т.е.
непрерывна справа (т.е. 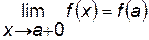 ), а в точке
), а в точке 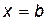 непрерывна слева (т.е.
непрерывна слева (т.е. 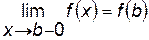 ).
).
Теорема (Вейерштрасса) о достижении наибольшего и наименьшего значения непрерывной функции на отрезке
Если функция непрерывна на отрезке, то она достигает на этом отрезке наибольшего и наименьшего значения.
Правило Лопиталя
Если 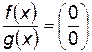 или
или 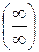 при
при 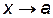 и существует
и существует 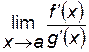 , то
, то 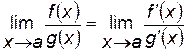 .
.
Теорема Ролля
Если функция 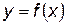 непрерывна на отрезке [
непрерывна на отрезке [ 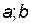 ], дифференцируема на (
], дифференцируема на (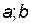 ) и на концах этого отрезка принимает одинаковые значения, то есть
) и на концах этого отрезка принимает одинаковые значения, то есть 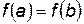 , то найдется точка
, то найдется точка 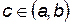 , такая, что
, такая, что 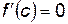 .
.
Теорема Лагранжа
Если функция 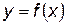 непрерывна на отрезке [
непрерывна на отрезке [ 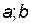 ], дифференцируема на (
], дифференцируема на (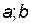 ), то найдется точка
), то найдется точка 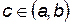 , такая, что
, такая, что 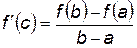 .
.
Теорема Коши
Если функции 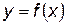 и
и 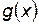 непрерывны на отрезке [
непрерывны на отрезке [ 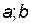 ], дифференцируема на (
], дифференцируема на (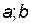 ) и
) и 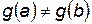 , то найдется точка
, то найдется точка 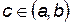 , такая, что
, такая, что 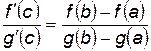 .
.
Комплексные числа
Определения. Комплексным числом называется выражение вида  , где
, где 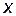 и
и  - действительные числа, а
- действительные числа, а  так называемая мнимая единица,
так называемая мнимая единица,  .
.
Число 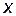 называется действительной частью комплексного числа
называется действительной частью комплексного числа  и обозначается
и обозначается  , а
, а  - мнимой частью
- мнимой частью  ,
,  .
.
Два комплексных числа  и
и  называются равными (
называются равными ( ) тогда и только тогда, когда равны их действительные части и равны их мнимые части:
) тогда и только тогда, когда равны их действительные части и равны их мнимые части: 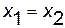 ,
, 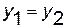 .
.
Два комплексных числа  и
и  отличающиеся лишь знаком мнимой части, называются сопряженными.
отличающиеся лишь знаком мнимой части, называются сопряженными.
Комплексное число  можно задавать с помощью радиус-вектора
можно задавать с помощью радиус-вектора  . Длина вектора
. Длина вектора  , изображающего комплексное число
, изображающего комплексное число  , называется модулем этого числа и обозначается
, называется модулем этого числа и обозначается  или
или  .
.
Величина угла между положительным направлением действительной оси и вектором  , изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Arg
, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Arg  или
или  .
.
Формула Муавра
 .
.
Арифметические действия
При умножении комплексных чисел модули перемножаются, а аргументы складываются.
При делении комплексных чисел делятся модули, а аргументы вычитаются.
При сложении комплексных чисел складываются действительные и мнимые части.
При вычитании комплексных чисел вычитаются действительные и мнимые части.
Неопределенный интеграл
Определение.  , если
, если  ,
,  - произвольная постоянная.
- произвольная постоянная.
Определенный интеграл
Определение.  , если этот предел не зависит от выбора точек
, если этот предел не зависит от выбора точек 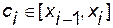 .
.
Здесь  ,
,  ,
, 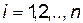 .
.
Теорема существования
Если функция 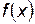 непрерывна, то определенный интеграл существует.
непрерывна, то определенный интеграл существует.
При вычислении определенного интеграла используется
Формула Ньютона-Лейбница
 , где
, где  .
.
Геометрический смысл определенного интеграла - это площадь криволинейной трапеции, ограниченной осью  , прямыми
, прямыми 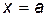 ,
,  , и графиком положительной функции
, и графиком положительной функции  .
.
Теорема о среднем значении
Если функция  непрерывна на отрезке [
непрерывна на отрезке [ 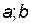 ], то существует точка
], то существует точка  [
[ 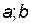 ] такая, что
] такая, что  .
.
Двойные интегралы
Определение. Пусть в замкнутой области  плоскости
плоскости  задана непрерывная функция
задана непрерывная функция 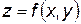 . Разобьем область
. Разобьем область  на
на  «элементарных областей»
«элементарных областей»  , площади которых обозначим через
, площади которых обозначим через 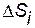 , а диаметры (наибольшее расстояние между точками области) - через
, а диаметры (наибольшее расстояние между точками области) - через  . В каждой области
. В каждой области  выберем произвольную точку
выберем произвольную точку  .
.
Тогда 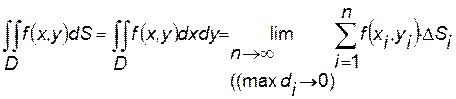 , если этот предел не зависит от способа выбора точек
, если этот предел не зависит от способа выбора точек 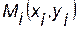 .
.
Теорема о среднем значении
Если функция  непрерывна в замкнутой области
непрерывна в замкнутой области  , площадь которой
, площадь которой  , то в этой области существует такая точка (
, то в этой области существует такая точка (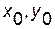 ), что
), что  .
.
Тройные интегралы
Определение. Пусть в замкнутой области  пространства
пространства  задана непрерывная функция
задана непрерывная функция 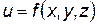 .
.
Разбив область  сеткой поверхностей на
сеткой поверхностей на  частей
частей  (
( ), и выбрав в каждой из них произвольную точку
), и выбрав в каждой из них произвольную точку  , составим интегральную сумму
, составим интегральную сумму  для функции
для функции  по области
по области  (здесь
(здесь  - объем элементарной области
- объем элементарной области  ). Если предел интегральной суммы существует при неограниченном увеличении числа
). Если предел интегральной суммы существует при неограниченном увеличении числа  таким образом, что каждая «элементарная область»
таким образом, что каждая «элементарная область»  стягивается в точку (т.е. диаметр области
стягивается в точку (т.е. диаметр области 
 ), то его называют тройным интегралом от функции
), то его называют тройным интегралом от функции  по области
по области  и обозначают
и обозначают  (или
(или  ). Таким образом, по определению, имеем:
). Таким образом, по определению, имеем:
 .
.
Теорема существования
Если функция  непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  , то предел интегральной суммы при
, то предел интегральной суммы при  и
и  существует и не зависит ни от способа разбиения области
существует и не зависит ни от способа разбиения области  на части, ни от выбора точек
на части, ни от выбора точек  в них.
в них.
Достаточные условия
В критической точке вычисляем  ,
,  ,
,  ,
,  .
.
Если 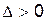 , то экстремум есть, причем при
, то экстремум есть, причем при  минимум, при
минимум, при  максимум.
максимум.
Если  , то экстремума нет.
, то экстремума нет.
Дифференциальные уравнения
Определения. Уравнение, связывающее независимую переменную, искомую функцию и ее производные, называется дифференциальным. 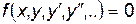 .
.
Уравнение вида  называется дифференциальным уравнением первого порядка, разрешенным относительно производной.
называется дифференциальным уравнением первого порядка, разрешенным относительно производной.
Задача Коши
Для уравнения  найти решение
найти решение  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
.
Теорема Пеано
Если  и
и  , функция
, функция  непрерывна в некоторой окрестности точки (
непрерывна в некоторой окрестности точки (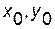 ), то существует
), то существует 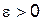 такое, что в интервале
такое, что в интервале  существует единственное решение уравнения
существует единственное решение уравнения  .
.
Аналогичная теорема имеет место и для систем дифференциальных уравнений.
Ряды
Определения. Числовым рядом (или просто рядом) называется выражение  , где
, где  - действительные или комплексные числа, называемые членами ряда,
- действительные или комплексные числа, называемые членами ряда,  - общим членом ряда.
- общим членом ряда.
Ряд считается заданным, если известен общий член ряда  , выраженный, как функция его номера:
, выраженный, как функция его номера:  .
.
Сумма первых  членов ряда называется
членов ряда называется  й частичной суммой ряда и обозначается через
й частичной суммой ряда и обозначается через  , то есть
, то есть  .
.
Если существует конечный предел  последовательности частичных сумм ряда, то этот предел называют суммой ряда, и говорят, что ряд сходится. Записывают
последовательности частичных сумм ряда, то этот предел называют суммой ряда, и говорят, что ряд сходится. Записывают  . Если
. Если  не существует или
не существует или  , то ряд называют расходящимся. Такой ряд суммы не имеет.
, то ряд называют расходящимся. Такой ряд суммы не имеет.
Интегральный признак Коши
Если  непрерывная положительная монотонно убывающая для
непрерывная положительная монотонно убывающая для 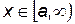 функция, причем
функция, причем  ,
,  , то ряд
, то ряд  и несобственный интеграл
и несобственный интеграл  одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Вычисление сумм рядов
Разложение на простейшие дроби
Пример. Вычислить  .
.
Решение.  .
.
Отсюда  при всех
при всех 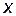 . При
. При  находим
находим  .
.  ,
,  . При
. При  находим
находим  .
.  ,
,  ,
,  .
.  .
.
Значит, 

 .
.
Использование разложений известных функций
Пример. Вычислить 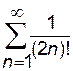 . Решение.
. Решение.  ;
;  .
. 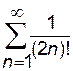
 .
.
Арифметическая прогрессия
Определение. Последовательность  называется арифметической прогрессией, если
называется арифметической прогрессией, если  , где
, где  - постоянное число, называемое разностью прогрессии.
- постоянное число, называемое разностью прогрессии.
Свойства.  .
.  .
.
Геометрическая прогрессия
Определение. Последовательность  называется геометрической прогрессией, если
называется геометрической прогрессией, если  , где
, где 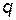 - постоянное число, называемое знаменателем прогрессии.
- постоянное число, называемое знаменателем прогрессии.
Свойства. 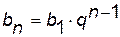 .
.  . Если
. Если  , то
, то  .
.
Рекомендуемая литература
1. Сборник докладов семинара «Вопросы методики подготовки к математическим олимпиадам в высшей школе» Вып. 1-11. Санкт-Петербург, Торгово-Промышленная Палата. 1999-2009 гг.
2. Беркович, Ф.Д. Задачи студенческих олимпиад с указаниями и решениями / Ф.Д.Беркович, В.С.Федий, В.И.Шлыков. - Ростов на Дону: Феникс, 2008.
3. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов. Том 1,2. / Н.С.Пискунов. – М.: Интеграл-Пресс, 2004.
4. Бугров, Я.С. Элементы линейной алгебры и аналитической геометрии / Я.С.Бугров, C.М.Никольский. – М.: Дрофа. 2004.
Игорь Борисович КОЖУХОВ,
Владимир Анатольевич СВЕНТКОВСКИЙ,
Татьяна Владимировна СОКОЛОВА
Московские городские
За 1996-2009 гг.
Редакторы: В.В.Виноградова
Компьютерная верстка: Н.А.Никитин
Подписано в печать 01.12.2010 г.
Формат 60´84/16. Бумага офсетная.
Гарнитура «Ариал». Печать офсетная.
Усл. печ. л. 18.3. Уч.-изд. л. 14,7.
Тираж 100 экз. Заказ 0027
Дополнение
Метод (принцип) математической индукции
Иногда, наблюдение указывает на проявление некоторой закономерности в зависимости от натурального  , начиная с некоторого. Естественно, появляется потребность доказать, что наблюдаемая закономерность проявляется при всех натуральных
, начиная с некоторого. Естественно, появляется потребность доказать, что наблюдаемая закономерность проявляется при всех натуральных  , начиная с некоторого известного номера. В этом случае часто применяется метод математической индукции.
, начиная с некоторого известного номера. В этом случае часто применяется метод математической индукции.
Этот метод эффективен, однако, сам по себе, не вскрывает причины проявления наблюдаемой закономерности, то есть сути явления.
1. Пусть логическое утверждение  верно при
верно при  .
.
2. Пусть из предположения, что  верно при
верно при 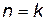 следует, что
следует, что  верно при
верно при  .
.
Тогда метод (принцип) математической индукции утверждает, что утверждение  верно при всех
верно при всех 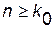 .
.
В самом деле, из 1,2 следует, что  - верно. Из 2) следует, что
- верно. Из 2) следует, что 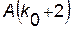 , так как
, так как  - верно. И т.д.
- верно. И т.д.
Пример. Доказать, что  .
.
При  , имеем:
, имеем: 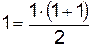 . Утверждение верно.
. Утверждение верно.
Пусть при  утверждение верно, т.е. равенство
утверждение верно, т.е. равенство  - верно.
- верно.
Тогда

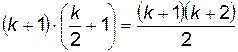 .
.
То есть утверждение верно и при  . Из принципа математической индукции, утверждение верно при всех
. Из принципа математической индукции, утверждение верно при всех  , a значит и при всех
, a значит и при всех  , так как то<
, так как то<


 , начиная с некоторого. Естественно, появляется потребность доказать, что наблюдаемая закономерность проявляется при всех натуральных
, начиная с некоторого. Естественно, появляется потребность доказать, что наблюдаемая закономерность проявляется при всех натуральных  верно при
верно при  .
. следует, что
следует, что  .
. .
. - верно. Из 2) следует, что
- верно. Из 2) следует, что 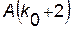 , так как
, так как  .
. , имеем:
, имеем: 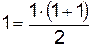 . Утверждение верно.
. Утверждение верно. утверждение верно, т.е. равенство
утверждение верно, т.е. равенство  - верно.
- верно.
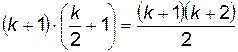 .
. . Из принципа математической индукции, утверждение верно при всех
. Из принципа математической индукции, утверждение верно при всех  , a значит и при всех
, a значит и при всех  .
. 



 .
. имеет
имеет  )
) .
. , то
, то  ,
,  ,…,
,…, 
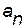 .
. без остатка разделится на
без остатка разделится на  .
.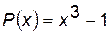 ;
; 
 , то есть
, то есть  делится без остатка на
делится без остатка на  .
. (здесь
(здесь  - определитель квадратной матрицы
- определитель квадратной матрицы  )
)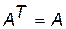
 , то
, то  - тоже диагональная матрица и
- тоже диагональная матрица и  .
. ,
, 
 , то
, то 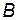 - тоже диагональная матрица и
- тоже диагональная матрица и  .
. (здесь
(здесь 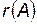 - ранг матрицы
- ранг матрицы 
 .
. .
.  . Имеем,
. Имеем,  .
.  . Отсюда
. Отсюда  . Аналогично доказывается, что
. Аналогично доказывается, что 
 . Теорема 2 доказана.
. Теорема 2 доказана. -й и
-й и  -й строки квадратной матрицы равносильно умножению слева на нее матрицы
-й строки квадратной матрицы равносильно умножению слева на нее матрицы
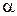 равносильно умножению слева на нее матрицы
равносильно умножению слева на нее матрицы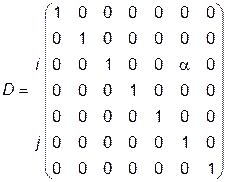
 равносильно умножению слева на нее матрицы
равносильно умножению слева на нее матрицы
 .
. ).
). получается из единичной матрицы сдвигом единицы в
получается из единичной матрицы сдвигом единицы в  . Положим
. Положим 
 , тогда
, тогда 

 получена из матрицы
получена из матрицы  перестановкой
перестановкой 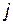 -ю строку, умноженную на число
-ю строку, умноженную на число  , то есть матрица
, то есть матрица  имеет вид:
имеет вид:
 ,
,

 прибавлением к
прибавлением к  -ой строки, умноженной на число
-ой строки, умноженной на число 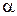 . Теперь, пусть нужно
. Теперь, пусть нужно 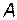 умножить на число
умножить на число  . То есть
. То есть  имеет вид:
имеет вид: . Пусть
. Пусть 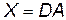 .
. .
.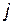 . Пусть
. Пусть  . Тогда, поскольку
. Тогда, поскольку , то
, то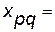
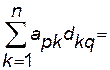
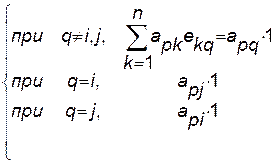
 получена перестановкой в матрице
получена перестановкой в матрице  . Тогда, поскольку
. Тогда, поскольку .
.

 . Это и значит, что в матрице
. Это и значит, что в матрице  -му столбцу прибавили
-му столбцу прибавили 
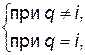
 .
. получена из матрицы
получена из матрицы  -го столбца на число
-го столбца на число 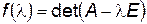 , то
, то 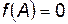 .
.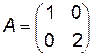 ,
, 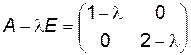 ,
, 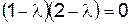 .
. 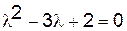 .
. 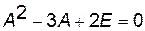 . Действительно,
. Действительно, 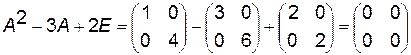 .
.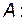
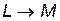 , где
, где  - векторные пространства, называется линейным оператором, если
- векторные пространства, называется линейным оператором, если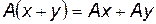 ,
, 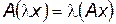 для всех
для всех 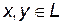 .
.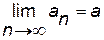 , то
, то 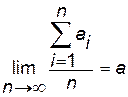 .
.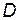 - одно из следующих множеств:
- одно из следующих множеств: 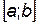 ,
, 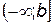 ,
, 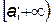 .
.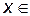
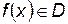 , функция
, функция 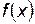 непрерывна, дифференцируема и выполняется неравенство
непрерывна, дифференцируема и выполняется неравенство 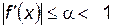 .
.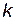 ,
, 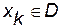 , то рекуррентная последовательность
, то рекуррентная последовательность 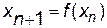 имеет пределом некоторое
имеет пределом некоторое 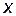 , причем
, причем 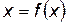 и
и 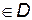 .
.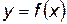 определена в точке
определена в точке 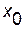 и в некоторой окрестности этой точки. Функция
и в некоторой окрестности этой точки. Функция 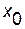 , если существует предел функции в этой точке и он равен значению функции в этой точке, то есть
, если существует предел функции в этой точке и он равен значению функции в этой точке, то есть 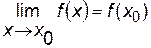 .
.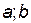 ), если она непрерывна в каждой точке этого интервала.
), если она непрерывна в каждой точке этого интервала.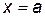 непрерывна справа (т.е.
непрерывна справа (т.е. 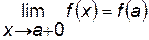 ), а в точке
), а в точке 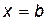 непрерывна слева (т.е.
непрерывна слева (т.е. 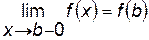 ).
).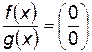 или
или 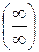 при
при 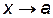 и существует
и существует 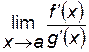 , то
, то 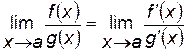 .
. непрерывна на отрезке [
непрерывна на отрезке [  ], дифференцируема на (
], дифференцируема на (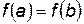 , то найдется точка
, то найдется точка 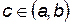 , такая, что
, такая, что 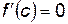 .
.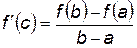 .
. непрерывны на отрезке [
непрерывны на отрезке [ 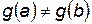 , то найдется точка
, то найдется точка 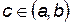 , такая, что
, такая, что 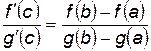 .
. , где
, где  - действительные числа, а
- действительные числа, а  так называемая мнимая единица,
так называемая мнимая единица,  .
. и обозначается
и обозначается  , а
, а  ,
,  .
. и
и  называются равными (
называются равными ( ) тогда и только тогда, когда равны их действительные части и равны их мнимые части:
) тогда и только тогда, когда равны их действительные части и равны их мнимые части: 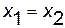 ,
, 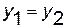 .
. и
и 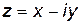 отличающиеся лишь знаком мнимой части, называются сопряженными.
отличающиеся лишь знаком мнимой части, называются сопряженными. . Длина вектора
. Длина вектора  , изображающего комплексное число
, изображающего комплексное число  или
или  .
. .
. .
. , если
, если  ,
,  - произвольная постоянная.
- произвольная постоянная. , если этот предел не зависит от выбора точек
, если этот предел не зависит от выбора точек 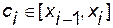 .
. ,
,  ,
, 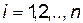 .
.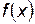 непрерывна, то определенный интеграл существует.
непрерывна, то определенный интеграл существует. , где
, где  , прямыми
, прямыми 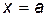 ,
,  , и графиком положительной функции
, и графиком положительной функции  .
. [
[  .
. плоскости
плоскости  задана непрерывная функция
задана непрерывная функция 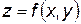 . Разобьем область
. Разобьем область  , площади которых обозначим через
, площади которых обозначим через 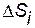 , а диаметры (наибольшее расстояние между точками области) - через
, а диаметры (наибольшее расстояние между точками области) - через  . В каждой области
. В каждой области  выберем произвольную точку
выберем произвольную точку  .
.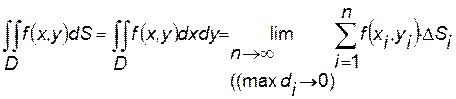 , если этот предел не зависит от способа выбора точек
, если этот предел не зависит от способа выбора точек 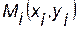 .
. непрерывна в замкнутой области
непрерывна в замкнутой области  , то в этой области существует такая точка (
, то в этой области существует такая точка (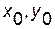 ), что
), что  .
. пространства
пространства  задана непрерывная функция
задана непрерывная функция 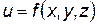 .
. (
( ), и выбрав в каждой из них произвольную точку
), и выбрав в каждой из них произвольную точку  , составим интегральную сумму
, составим интегральную сумму  для функции
для функции  по области
по области  (здесь
(здесь  - объем элементарной области
- объем элементарной области 
 ), то его называют тройным интегралом от функции
), то его называют тройным интегралом от функции  по области
по области  (или
(или  ). Таким образом, по определению, имеем:
). Таким образом, по определению, имеем: .
. непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  и
и  существует и не зависит ни от способа разбиения области
существует и не зависит ни от способа разбиения области  на части, ни от выбора точек
на части, ни от выбора точек  в них.
в них. ,
,  ,
,  ,
,  .
.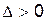 , то экстремум есть, причем при
, то экстремум есть, причем при  минимум, при
минимум, при  максимум.
максимум. , то экстремума нет.
, то экстремума нет.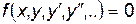 .
. называется дифференциальным уравнением первого порядка, разрешенным относительно производной.
называется дифференциальным уравнением первого порядка, разрешенным относительно производной. , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
. и
и  , функция
, функция  непрерывна в некоторой окрестности точки (
непрерывна в некоторой окрестности точки (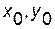 ), то существует
), то существует 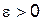 такое, что в интервале
такое, что в интервале  существует единственное решение уравнения
существует единственное решение уравнения  .
. , где
, где  - действительные или комплексные числа, называемые членами ряда,
- действительные или комплексные числа, называемые членами ряда,  - общим членом ряда.
- общим членом ряда. .
. й частичной суммой ряда и обозначается через
й частичной суммой ряда и обозначается через  , то есть
, то есть  .
. последовательности частичных сумм ряда, то этот предел называют суммой ряда, и говорят, что ряд сходится. Записывают
последовательности частичных сумм ряда, то этот предел называют суммой ряда, и говорят, что ряд сходится. Записывают  . Если
. Если  не существует или
не существует или  , то ряд называют расходящимся. Такой ряд суммы не имеет.
, то ряд называют расходящимся. Такой ряд суммы не имеет. непрерывная положительная монотонно убывающая для
непрерывная положительная монотонно убывающая для 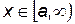 функция, причем
функция, причем  , то ряд
, то ряд  и несобственный интеграл
и несобственный интеграл  одновременно сходятся или расходятся.
одновременно сходятся или расходятся. .
. .
. при всех
при всех  находим
находим  .
.  ,
,  . При
. При  находим
находим  .
.  ,
,  ,
,  .
.  .
.

 .
.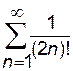 . Решение.
. Решение.  ;
;  .
.  .
. называется арифметической прогрессией, если
называется арифметической прогрессией, если  , где
, где  - постоянное число, называемое разностью прогрессии.
- постоянное число, называемое разностью прогрессии. .
.  .
. называется геометрической прогрессией, если
называется геометрической прогрессией, если  , где
, где 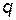 - постоянное число, называемое знаменателем прогрессии.
- постоянное число, называемое знаменателем прогрессии.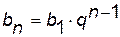 .
.  . Если
. Если  , то
, то  .
.